۰
subtitle
ارسال: #۱
حل و برسی سوالات ساختمان داده ۹۱ مهندسی کامپیوتر
در این تاپیک سوالات ساختمان داده ۹۱ بررسی خواهد شد.
سوالات پیوست شدن.
پاسخ های سنجش:
۴۷- ۳
۴۸- ۴
۴۹- ۳
۵۰- ۱
۵۱- ۲
۵۲- ۳
سوالات پیوست شدن.
پاسخ های سنجش:
۴۷- ۳
۴۸- ۴
۴۹- ۳
۵۰- ۱
۵۱- ۲
۵۲- ۳
۰
ارسال: #۲
ساختمان داده ۹۱ مهندسی کامپیوتر
من استدلالهای دوستان خوبم رو با دقت خوندم به نظرم این استدلال پایین از دوستمون از همه محکم تر بود
ایشون منظور سوال رو هم قشنگ تعبیر کردند که اون ایهام توی ذهن من رفع شد
به نظرم جوابشون قانع کنندست اگه با دقت بخونید
حالا طراح میمرد دو بار اسم تابع جی رو نیاره از اول همینو بگه
"خلاصه اش اینه که آیا می شه هیچ f ی رو مثال زد بطوریکه جواب بشه g ."
ایشون منظور سوال رو هم قشنگ تعبیر کردند که اون ایهام توی ذهن من رفع شد
به نظرم جوابشون قانع کنندست اگه با دقت بخونید
(۲۹ بهمن ۱۳۹۰ ۰۴:۰۲ ب.ظ)yaali نوشته شده توسط: سوال گفته برای چند تا از توابع زیر (همون g ها )می شه حداقل یک f مثال زد بطوریکه پاسخ بشه g .
خلاصه اش اینه که آیا می شه هیچ f ی رو مثال زد بطوریکه جواب بشه g .
خوب اگه ما بتونیم حتی یک مثال هم بیاریم ، کافیه.
اگه f=n بگیریم جواب می شه تتای n^2 .
اگه f= n^3 بگیریم جواب می شه تتای n^3
اگه f=n^2logn بگیریم جواب می شه تتای n^2logn^2
اما هیچ f ی رو نمی شه مثال زد بطوریکه جواب بشه nlogn
حالا طراح میمرد دو بار اسم تابع جی رو نیاره از اول همینو بگه
"خلاصه اش اینه که آیا می شه هیچ f ی رو مثال زد بطوریکه جواب بشه g ."
۰
ارسال: #۳
RE: ساختمان داده ۹۱ مهندسی کامپیوتر
در مورد سوال ۵۲ که واقعا اسون تر از این نمیشد سوال داد همون گزینه ۳ یعنی ۵۸ درسته.
دوستان کسی سوال ۴۹ رو جواب نداده؟؟؟چند میشه؟هرکی جواب داده با راه حل بگه لطفا
دوستان کسی سوال ۴۹ رو جواب نداده؟؟؟چند میشه؟هرکی جواب داده با راه حل بگه لطفا
۰
ارسال: #۴
ساختمان داده ۹۱ مهندسی کامپیوتر
(۲۹ بهمن ۱۳۹۰ ۰۸:۳۹ ب.ظ)fmka2f نوشته شده توسط: در مورد سوال ۵۲ که واقعا اسون تر از این نمیشد سوال داد همون گزینه ۳ یعنی ۵۸ درسته.۱۱ رو میذاری ریشه (مجبور هستیم)
دوستان کسی سوال ۴۹ رو جواب نداده؟؟؟چند میشه؟هرکی جواب داده با راه حل بگه لطفا
زیر درخت سمت راست:
سه عنصر برای سمت راست از ده تا انتخاب میکنید * دو حالتی که این عناصر میتونند قرار بگیرند (عنصر بزرگتر ریشه و دو حالت برای عناصر زیری
زیر درخت سمت چپ:
به همون روال قبلی
ادامه میدی و کل حالات رو در هم ضرب میکنی پاسخ ۱۱۵۲۰
ارسال: #۵
RE: ساختمان داده ۹۱ مهندسی کامپیوتر
[/quote]
۱۱ رو میذاری ریشه (مجبور هستیم)
زیر درخت سمت راست:
سه عنصر برای سمت راست از ده تا انتخاب میکنید * دو حالتی که این عناصر میتونند قرار بگیرند (عنصر بزرگتر ریشه و دو حالت برای عناصر زیری
زیر درخت سمت چپ:
به همون روال قبلی
ادامه میدی و کل حالات رو در هم ضرب میکنی پاسخ ۱۱۵۲۰
[/quote]
خوب این روش با اینکه درسته ولی کل جلسه زمان میبره...راه حلش همینه فقط؟؟؟روش خاصی نداشت احیانا؟
۱۱ رو میذاری ریشه (مجبور هستیم)
زیر درخت سمت راست:
سه عنصر برای سمت راست از ده تا انتخاب میکنید * دو حالتی که این عناصر میتونند قرار بگیرند (عنصر بزرگتر ریشه و دو حالت برای عناصر زیری
زیر درخت سمت چپ:
به همون روال قبلی
ادامه میدی و کل حالات رو در هم ضرب میکنی پاسخ ۱۱۵۲۰
[/quote]
خوب این روش با اینکه درسته ولی کل جلسه زمان میبره...راه حلش همینه فقط؟؟؟روش خاصی نداشت احیانا؟
۰
ارسال: #۶
ساختمان داده ۹۱ مهندسی کامپیوتر
(۲۹ بهمن ۱۳۹۰ ۰۳:۳۶ ب.ظ)Masoud05 نوشته شده توسط: این سوال رو خیلی بد مطرح کرده طراح ، انگار میخواسته تابع بازگشتی براش بنویسهواقعا" این طراحی که خودش سؤال رو نمیتونه درست بیان کنه از کجا آوردن! فکر کنم استاد ادبیات بوده خواسته ایهام بکار ببره ببینه ما میفمیم یا نه!!!
واقعا" متاسفم برای سازمان سنجش، سال به سال کج سلیقگی و نا همگونی و غلط و اشتباه جای کم شدن داره بیشتر میشه!
البته کلا" تو این سیستم توقعی هم نمیشه داشت، اگه همه چی خوب و منظم و عالی باشه باید تعجب کرد!
۰
ارسال: #۷
ساختمان داده ۹۱ مهندسی کامپیوتر
واقعا از دوستانی که در تفهیم سوال ۴۷ به بقیه کمک کردن ممنونم.
دو روزه دارم به یکی توضیح میدم که برادر من صورت سوال این نیست که تو میگی اما تو کتش نمیرفت.
تا اینکه از توضیحات دوستان استفاده کردم و قانعش کردم که جواب ۳ میشه !

دو روزه دارم به یکی توضیح میدم که برادر من صورت سوال این نیست که تو میگی اما تو کتش نمیرفت.
تا اینکه از توضیحات دوستان استفاده کردم و قانعش کردم که جواب ۳ میشه !

ارسال: #۸
RE: ساختمان داده ۹۱ مهندسی کامپیوتر
(۲۹ بهمن ۱۳۹۰ ۰۹:۳۳ ب.ظ)fardin_ss نوشته شده توسط: واقعا از دوستانی که در تفهیم سوال ۴۷ به بقیه کمک کردن ممنونم.
دو روزه دارم به یکی توضیح میدم که برادر من صورت سوال این نیست که تو میگی اما تو کتش نمیرفت.
تا اینکه از توضیحات دوستان استفاده کردم و قانعش کردم که جواب ۳ میشه !
ولی شک نکن که یک میشه کلید بیاد میفهمی

۰
ارسال: #۹
ساختمان داده ۹۱ مهندسی کامپیوتر
در مورد سوال ۱ ساختمان:
من خودم ۳ تا رو زدم
ولی چطور می گین گزینه ۴ نمیشه؟ هیچ کس در این مورد هم حرفی نزده!
برای N^2 و N^3 که قضیه راحته و از مستر میشه رفت
برای N^2 log(n)^2 هم من نفهمیدم چه استدالالی دوستان کردن ولی خوب از حل معادله با F(n)= N^2 log n به همین جواب میرسیم. (این کاملا اتفاقی هست ها) ولی از کجا معلوم که نمیشه F ای پیدا کرد که جوابش nlogn نشه؟ دقت کنید که نمی تونید از مستر استفاده کنید.
من خودم ۳ تا رو زدم
ولی چطور می گین گزینه ۴ نمیشه؟ هیچ کس در این مورد هم حرفی نزده!
برای N^2 و N^3 که قضیه راحته و از مستر میشه رفت
برای N^2 log(n)^2 هم من نفهمیدم چه استدالالی دوستان کردن ولی خوب از حل معادله با F(n)= N^2 log n به همین جواب میرسیم. (این کاملا اتفاقی هست ها) ولی از کجا معلوم که نمیشه F ای پیدا کرد که جوابش nlogn نشه؟ دقت کنید که نمی تونید از مستر استفاده کنید.
ارسال: #۱۰
RE: ساختمان داده ۹۱ مهندسی کامپیوتر
(۳۰ بهمن ۱۳۹۰ ۰۱:۴۳ ق.ظ)imi نوشته شده توسط: در مورد سوال ۱ ساختمان:
من خودم ۳ تا رو زدم
ولی چطور می گین گزینه ۴ نمیشه؟ هیچ کس در این مورد هم حرفی نزده!
برای N^2 و N^3 که قضیه راحته و از مستر میشه رفت
برای N^2 log(n)^2 هم من نفهمیدم چه استدالالی دوستان کردن ولی خوب از حل معادله با F(n)= N^2 log n به همین جواب میرسیم. (این کاملا اتفاقی هست ها) ولی از کجا معلوم که نمیشه F ای پیدا کرد که جوابش nlogn نشه؟ دقت کنید که نمی تونید از مستر استفاده کنید.
چون خود (۹t(n/3 که میشه n^2 از nlogn بزرگتره
۰
۰
ارسال: #۱۲
RE: ساختمان داده ۹۱ مهندسی کامپیوتر
۰
ارسال: #۱۳
ساختمان داده ۹۱ مهندسی کامپیوتر
دوستان به نظر من ۴۷ گزینه ۳ میشه
به جز n lg n که کمتر از n^2 بود بقیش رو میشد f(n انتخاب کرد
بابا یکی به مدیر سایت بگه پدرمون در میاد بخوایم یه پرانتز باز یا بسته درست پست کنیم
سایتو درستش کنین
به جز n lg n که کمتر از n^2 بود بقیش رو میشد f(n انتخاب کرد
بابا یکی به مدیر سایت بگه پدرمون در میاد بخوایم یه پرانتز باز یا بسته درست پست کنیم
سایتو درستش کنین
ارسال: #۱۴
RE: ساختمان داده ۹۱ مهندسی کامپیوتر
(۳۰ بهمن ۱۳۹۰ ۰۴:۰۷ ب.ظ)mjzarrin نوشته شده توسط: دوستان به نظر من ۴۷ گزینه ۳ میشه
به جز n lg n که کمتر از n^2 بود بقیش رو میشد f(n انتخاب کرد
بابا یکی به مدیر سایت بگه پدرمون در میاد بخوایم یه پرانتز باز یا بسته درست پست کنیم
سایتو درستش کنین
اطلاعاتتون راجبه درس الگوریتم و داده و این مبحث فک میکنم کافی نیس،
سایت مشکلی نداره تو [Tex] بذار فرمولاتو اون پایین...
۰
ارسال: #۱۵
 ساختمان داده ۹۱ مهندسی کامپیوتر
ساختمان داده ۹۱ مهندسی کامپیوتر
بله ۴۷ گزینه ۳درسته من مطمینم
سوال ۴۹هم اصلآ حل نکردم احساس کردم یکی گفت گزینه ۳ رو یعنی ۱۱۵۲۰رو بزن خوب شد حل نکردم به جواب نمی رسیدم

سوال ۴۹هم اصلآ حل نکردم احساس کردم یکی گفت گزینه ۳ رو یعنی ۱۱۵۲۰رو بزن خوب شد حل نکردم به جواب نمی رسیدم


۰
ارسال: #۱۶
RE: ساختمان داده ۹۱ مهندسی کامپیوتر
۵۲- جواب ۵۹ است اگه شما درختی با عمق ۶ رسم کنید و عدد ۶۴ رو به ریشه بدید و به سمت راسترین فرزند هم عدد ۶۳ و به سمت راسترین بعدی ۵۲ و همین طور به سمت پایین بروید آخرین برگ سمت راست درخت مقدار ۵۹ می گیره.!! این درخت یک درخته پر هست.
ارسال: #۱۷
RE: ساختمان داده ۹۱ مهندسی کامپیوتر
(۳۰ بهمن ۱۳۹۰ ۱۰:۱۹ ب.ظ)fazel-d نوشته شده توسط: ۵۲- جواب ۵۹ است اگه شما درختی با عمق ۶ رسم کنید و عدد ۶۴ رو به ریشه بدید و به سمت راسترین فرزند هم عدد ۶۳ و به سمت راسترین بعدی ۵۲ و همین طور به سمت پایین بروید آخرین برگ سمت راست درخت مقدار ۵۹ می گیره.!! این درخت یک درخته پر هست.
قبلا درخت رو رسم کردیم و ۵۸ شد . صفحات قبل رو بخونید
۰
ارسال: #۱۸
RE: ساختمان داده ۹۱ مهندسی کامپیوتر
سوال ۵۱ را با لیست پیوندی می توان ساخت که هزینه درج n عنصر در آن از مرتبه O(n باشه
نظر سایر دوستان چیه؟
اگر چه توسط ماهان و ... nlgn بدست اومده
نظر سایر دوستان چیه؟
اگر چه توسط ماهان و ... nlgn بدست اومده
ارسال: #۱۹
RE: ساختمان داده ۹۱ مهندسی کامپیوتر
۰
ارسال: #۲۰
ساختمان داده ۹۱ مهندسی کامپیوتر
دوست عزیز نگفته بزرگترین برگ بلکه گفته بزرگترین گره در سطح آخر در واقع ۵۹ برگ در سطح یکی به آخر هست نه سطح آخر
۰
ارسال: #۲۱
ساختمان داده ۹۱ مهندسی کامپیوتر
gn میشد سه تا اون سوال هم ۵۸ میشد و تکرلری بود سوال it83 بود!
۰
ارسال: #۲۲
RE: ساختمان داده ۹۱ مهندسی کامپیوتر
۴۷- گزینه ۳ درسته، البته اگر تخیلی فکر کنیم ۴ هم میشه. بعضی از کسانی که ۱ رو درست می دونن احتمالا مثل من اشتباهی لگاریتم ۹ در مبنای ۳ را ۳ گرفتن.
۴۹- گزینه ۳ با استفاده از اصل ضرب و تعریف بازگشتی حل میشه: تعداد حالات ممکن در هر گره داخلی فرضی روی این درخت عبارتست از:
تعداد حالات زیر درخت چپ * تعداد حالات زیر درخت راست * تعداد حالات تقسیم اعداد در دو زیر درخت
و هر برگ تنها یک حالت دارد.
از ریشه که به سمت پایین میرویم تنها "تعداد حالات تقسیم اعداد در دو زیر درخت" را درون نودهای داخلی می نویسیم، وقتی اعداد کامل شدند کافی است همه اعداد درخت را در هم ضرب کنیم!
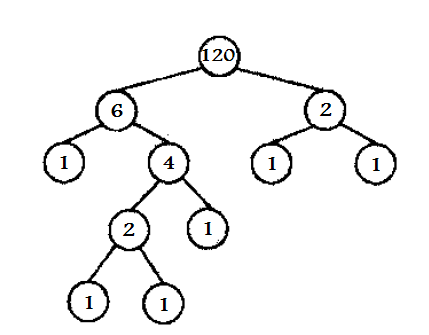
۵۰- در وهله اول گزینه های ۲ و ۴ حذف میشه چون ما می دونیم که چنین کدی مرتبه ۲ هست نه فاکتوریلی!
۴۹- گزینه ۳ با استفاده از اصل ضرب و تعریف بازگشتی حل میشه: تعداد حالات ممکن در هر گره داخلی فرضی روی این درخت عبارتست از:
تعداد حالات زیر درخت چپ * تعداد حالات زیر درخت راست * تعداد حالات تقسیم اعداد در دو زیر درخت
و هر برگ تنها یک حالت دارد.
از ریشه که به سمت پایین میرویم تنها "تعداد حالات تقسیم اعداد در دو زیر درخت" را درون نودهای داخلی می نویسیم، وقتی اعداد کامل شدند کافی است همه اعداد درخت را در هم ضرب کنیم!

۵۰- در وهله اول گزینه های ۲ و ۴ حذف میشه چون ما می دونیم که چنین کدی مرتبه ۲ هست نه فاکتوریلی!
۰
۰
ارسال: #۲۴
RE: ساختمان داده ۹۱ مهندسی کامپیوتر
سلام.کلیدای سنجش هم اومد.اما مثکه سوال ۵۰ رو اشتباه زده جوابشو.به نظر شما نزده؟فکر کنم ۳ بشه، ولی زده ۱/
یه اعتراض بذاریم شاید درستش کردن!

یه اعتراض بذاریم شاید درستش کردن!
ارسال: #۲۵
RE: ساختمان داده ۹۱ مهندسی کامپیوتر
۰
ارسال: #۲۶
ساختمان داده ۹۱ مهندسی کامپیوتر
(۰۸ اسفند ۱۳۹۰ ۰۹:۳۰ ق.ظ)mj_shbn نوشته شده توسط:برای n=2 ، جواب ۴ و برای n=3 ، جواب ۹ بدست میاد. گزینه ۳ درسته.(08 اسفند ۱۳۹۰ ۰۱:۰۱ ق.ظ)mohammad_13690 نوشته شده توسط:آره الان که برای n=3 و n=2 امتحان کردم، دیدم شما درست زدید. نمی دونم چرا سر جلسه من گزینه ۳ رو بدست آوردم؟!!!!(08 اسفند ۱۳۹۰ ۱۲:۰۷ ق.ظ)mj_shbn نوشته شده توسط: سلام.کلیدای سنجش هم اومد.اما مثکه سوال ۵۰ رو اشتباه زده جوابشو.به نظر شما نزده؟فکر کنم ۳ بشه، ولی زده ۱/
یه اعتراض بذاریم شاید درستش کردن!
من هم زدم ۱
اما ماهان و مدرسان شریف هم مثل شما زدن ۳
راستی چرا شما میگید ۳؟
۰
ارسال: #۲۷
ساختمان داده ۹۱ مهندسی کامپیوتر
۰
ارسال: #۲۸
ساختمان داده ۹۱ مهندسی کامپیوتر
به نظرم ابن سوال مربوط به حذف و درج داده در ساختمان داده های جدا از هم باشه.(فصل۲۱ کورمن)
درج یک داده از مرتبه logn ، برای درج کل عناصر از مرتبه nlogn خواهد بود، فکر نمی کنم بشه این کار رو با هزینه کمتری انجام داد.
درج یک داده از مرتبه logn ، برای درج کل عناصر از مرتبه nlogn خواهد بود، فکر نمی کنم بشه این کار رو با هزینه کمتری انجام داد.
ارسال: #۲۹
RE: ساختمان داده ۹۱ مهندسی کامپیوتر
(۱۴ اسفند ۱۳۹۰ ۱۲:۲۸ ب.ظ)anyone نوشته شده توسط: به نظرم ابن سوال مربوط به حذف و درج داده در ساختمان داده های جدا از هم باشه.(فصل۲۱ کورمن)
درج یک داده از مرتبه logn ، برای درج کل عناصر از مرتبه nlogn خواهد بود، فکر نمی کنم بشه این کار رو با هزینه کمتری انجام داد.
آخه با توضیحاتی که تو صورت سوال داده برای درج عنصر nام همه n-1 عنصر قبلی باید مجددا درج بشن که هزینه اش برای n عنصر بیشتر از nlgn میشه، برای هر عنصر n و برای n عنصر میشه n^2
۰
ارسال: #۳۰
ساختمان داده ۹۱ مهندسی کامپیوتر
به نظر من هم توضیحات خیلی واضع نبودند ولی به نظرم این کار با این ساختمان داده قابل انجامه پس این هزینه منطقیه اما در مورد هزینه کمتر نظری ندارم
۰
ارسال: #۳۲
RE: ساختمان داده ۹۱ مهندسی کامپیوتر
(۱۴ اسفند ۱۳۹۰ ۰۵:۵۸ ب.ظ)abcd1234 نوشته شده توسط: کسی میتونه سوال ۵۱ رو توضیح بده؟
سلام به همه دوستان خوب هم رشته ای،

جواب سوال ۵۱ از رابطه بازگشتی قابل محاسبه ست
قبول کنید میشه حدس زد T(n)=n+2*T(n/2) l
اگه قبول نکنید مجبورید این متن طولانی رو بخونید

_____
صورت سوال: ساختار داده شامل مجموعه های Si است که هرکدام صفر یا l 2^n عضو دارند...
فرض کنید چهار تا S داریم با این ترتیب تعداد عناصر [۰][۰][۰][۰]
یکی یکی اضافه کردن هشت عنصر را بررسی می کنیم
[۱][۰][۰][۰]
[۰][۲][۰][۰]
[۱][۲][۰][۰]
[۰][۰][۴][۰]
[۱][۰][۴][۰]
[۰][۲][۴][۰]
[۱][۲][۴][۰]
[۰][۰][۰][۸]
سریعا متوجه میشویم:
چون هر مجموعه صفر یا ۲n^ عضو دارد هنگامی که k عضو در ساختار داده هست، اگر k را با مجموع توان های دو بنویسم، هر کدام از آن اعداد تعداد یکی از S هاست (مثلا ۱۰۰=۶۴+۳۲+۴، پس هنگامی که صد عنصر داریم سه تا از S ها تعداد ۴ و ۳۲ و ۶۴ وبقیه صفر دارند) (و بدیهی است این یک تناظر با باینری نوشتن عدد دارد ۱۰۰D=1100100B)
اگه بیشتر تو این هشت مرحله دقت کنیم متوجه میشیم:
S1 همیشه یا خالی ست یا ۲^۱ عنصر دارد، اما S2 یا خالی ست یا ۲^۲ عضو دارد و S3 2^3 (باز هم تناظر با باینری نوشتن عدد)
اما چطور میفهمیم nlogn:
توضیح میدم چطوری T(n)=n+2*T(n/2) l
فرض کنید n یک عدد توان دو هست، برای نوشتن n عنصر در ساختار ابتدا با صرف مقداری هزینه n/2 عنصر در ساختار میریزیم که پر و خالی بودن مجموعه های S به این صورت در میان: ۰۰۰///۱۰۰۰۰ (توضیح دادم تناظر با باینری نوشتن)
حالا می خواهیم n/2 عنصر دیگه رو اضافه کنیم، همونقدر هزینه میبره که قبلا برد، اما آخرین عنصرش به اندازه n هزینه بیشتر میبره (چون صورت سوال گفته هزینه انتقال برابر مجموع تعداد عناصر است) و این همون T(n)=n+2*T(n/2) l هست
مجبورید قبول کنید که اگه n توان دو هم نبود همین رابطه برقرار بود (اثباتش دور از ذهن نیست)
شاید می پرسید چجوری اینا رو سر جلسه میفهمیدیم جوابش هم اینه که این تحلیلا برای بعد جلسه ست و من سر جلسه نتونستم فکر کنم نزدم
۰
ارسال: #۳۳
ساختمان داده ۹۱ مهندسی کامپیوتر
مگه تفاوتی می کنه با لیست پیوندی باشه یا آرایه؟
طبق توضیح من هم وقتی یک عنصر توی Sk ریخته میشه، S0 تا Sk-1 خالی میشه و من متوجه نشدم چجوری از این ها به O(n رسیدید. میشه بیشتر توضیح بدید
طبق توضیح من هم وقتی یک عنصر توی Sk ریخته میشه، S0 تا Sk-1 خالی میشه و من متوجه نشدم چجوری از این ها به O(n رسیدید. میشه بیشتر توضیح بدید
ارسال: #۳۴
RE: ساختمان داده ۹۱ مهندسی کامپیوتر
(۱۶ اسفند ۱۳۹۰ ۱۱:۴۸ ب.ظ)mohammad_13690 نوشته شده توسط:اگر در هر مرحله لیست پیوندی را به صورت زنجیر در نظر بگیریم(نه لیست رنجیری ، با لیست زنجیری هم "ترکیب آرایه و لیست های پیوندی " می توان با o(n پیاده سازی کرد ) به جای حذف s0 تا sk-1 می توان زنجیر را شکست و انتقال داد (بدون اضافه شدن هزینه حذف عناصر- تنها با تغییر اتصال ها) در نتیجه هزینه افزودن n عنصر باقی می ماند(16 اسفند ۱۳۹۰ ۱۰:۲۴ ب.ظ)n_alaie نوشته شده توسط:مگه تفاوتی می کنه با لیست پیوندی باشه یا آرایه؟
طبق توضیح من هم وقتی یک عنصر توی Sk ریخته میشه، S0 تا Sk-1 خالی میشه و من متوجه نشدم چجوری از این ها به O(n رسیدید. میشه بیشتر توضیح بدید
Can I see some ID?
Feeling left out?
نگران نباش، فقط روی این لینک برای ثبت نام کلیک کن. رمزت رو فراموش کردی؟ اینجا به یادت میاریم! close



 در حال حاضر)
در حال حاضر)
 )
)