۰
subtitle
ارسال: #۱
نکات و فرمولهایی در مورد سری فوریه

خب از این بعد سعی بکنیم درکنار حفظ فرمول های ریاضی ، مفاهیم رو هم بفهمیم ؛ به کمک شما سعی می کنم تا جایی که امکان داره فرمول ها رو باز کنم تا برای خودم و شما جا بیوفته ، خوشحال میشم اگر فایلی که خودتون نوشتین رو اینجا آپلود کنید (کپی از ویکی نکنید)
تنها هدفم از ایجاد این تاپیک علاقه به ریاضیات و علاقه مند کردن دیگران هست !
۰
ارسال: #۲
۱-Complex
با اجازه شما از اعداد مختلط شروع می کنیم ؛ ۳ مطلب رو گذاشتم که ریشه های مختلط ، وارون یا معکوس عدد مختلط و فرم قطبی هست ، سعی کردم توضیح بدم که چرا همچین مفاهیمی رو ابداع کردند حالا آپلود کنید خودتون می فهمید:
۰
ارسال: #۳
RE: Learn Engineering Mathematics concepts
[tex]\lim_{z\rightarrow i}Sin(z)=\lim_{z\rightarrow (0,1)}\frac{e^{i.i}-e^{-i.i}}{2i}=\frac{e^{-1}-e^{1}}{2i}=\frac{-(e^{-1}-e^{-1})}{2i}*\frac{i}{i}=i\frac{e^{1}-e^{-1}}{2}=iSinH(1)[/tex]
در اینجا سعی کردم lim یک تابع ساده مثله sin رو بنویسم زمانی که به سمت i میل می کنه ما i رو می توانیم به صورت زوج مرتب ۰,۱ نوشتیم که ۱ ضریب i هست--------------------------------------------------
اگر کوشی ریمان رو به خاطر بیارین ما تو اونجا گفتیم اگر تابع ما مشتق پذیر باشد به صورت زیر فرمول می شود :
[tex]{f(z)}'=(u_{r} iv_{r}).e^{-i\Theta }[/tex]
شاید برای کسی سوال پیش بیاید که چرا ما یک ضریب e پشت پرانتز داریم ! جواب اش این است که اگر این ضریب پشت پرانتز نباشد به مشتق تابع مختلط نمی رسیم.
-------------------------------------------------
یکی از فرمول های طلایی ریاضی مهندسی و ریاضی ۱ فرمول زیر است که به کمک همین فرمول جواب یکی از تست های کنکور به راحتی حل می شد و می شود و خواهد شد:
[tex]a^{b}\leftrightarrow e^{b Ln a}[/tex]
تست : [tex]i^{i}=?[/tex]
جواب :
[tex]i^{i}=e^{i Ln i}=e^{^{i.i. \frac{\Pi}{2}}}=e^{-\frac{\Pi }{2}}[/tex]
تست : [tex]i^{i}=?[/tex]
جواب :
[tex]i^{i}=e^{i Ln i}=e^{^{i.i. \frac{\Pi}{2}}}=e^{-\frac{\Pi }{2}}[/tex]

ارسال: #۴
RE: Learn Engineering Mathematics concepts
(۰۷ اردیبهشت ۱۳۹۱ ۰۱:۱۵ ب.ظ)Pakniat نوشته شده توسط:[tex]\lim_{z\rightarrow i}Sin(z)=\lim_{z\rightarrow (0,1)}\frac{e^{i.i}-e^{-i.i}}{2i}=\frac{e^{-1}-e^{1}}{2i}=\frac{-(e^{-1}-e^{-1})}{2i}*\frac{i}{i}=i\frac{e^{1}-e^{-1}}{2}=iSinH(1)[/tex]در اینجا سعی کردم lim یک تابع ساده مثله sin رو بنویسم زمانی که به سمت i میل می کنه ما i رو می توانیم به صورت زوج مرتب ۰,۱ نوشتیم که ۱ ضریب i هست
--------------------------------------------------
اگر کوشی ریمان رو به خاطر بیارین ما تو اونجا گفتیم اگر تابع ما مشتق پذیر باشد به صورت زیر فرمول می شود :
[tex]{f(z)}'=(u_{r} iv_{r}).e^{-i\Theta }[/tex]
شاید برای کسی سوال پیش بیاید که چرا ما یک ضریب e پشت پرانتز داریم ! جواب اش این است که اگر این ضریب پشت پرانتز نباشد به مشتق تابع مختلط نمی رسیم.
-------------------------------------------------
یکی از فرمول های طلایی ریاضی مهندسی و ریاضی ۱ فرمول زیر است که به کمک همین فرمول جواب یکی از تست های کنکور به راحتی حل می شد و می شود و خواهد شد:
[tex]a^{b}\leftrightarrow e^{b Ln a}[/tex]
تست : [tex]i^{i}=?[/tex]
جواب :
[tex]i^{i}=e^{i Ln i}=e^{^{i.i. \frac{\Pi}{2}}}=e^{-\frac{\Pi }{2}}[/tex]
ببخشید فقط یکجا توی حد گرفتن یک اشتباه کوچیک توی نوشتن داشتی و بجای توان ۱ نوشتی توان ۱- لطفا درستش کن. مرسی
(۲۹ تیر ۱۳۹۱ ۰۷:۰۱ ب.ظ)Pakniat نوشته شده توسط: همان طور که می دونید رفتار تابع می تونه به ۲ صورت مورد بررسی قرار بگیره : ۱- رفتار منظم ۲- رفتار های نامنظم
توابع نا منظم رو نمیشه از طریق سری فوریه توصیف کرد اما اگر همون تابع در دامنه (+∞و-∞) انتگرال پذیر باشه می تونیم با استفاده از انتگرال فوریه Sin,Cos رفتار اون تابع رو به نحوی شبیه سازی کنیم ؛
[tex]\int_{0}^{\infty }(A(\omega )\cos \omega x b(\omega ) \sin \omega X)d\omega[/tex]
در سری فوریه هر چقدر [tex]\sum_{i=1}^{n}[/tex] بیشتر نوشته بشه همگرایی مشهود تر میشه
این جمله که در آخر گفتید هر چقدر [tex]\sum_{i=1}^{n}[/tex] بیشتر نوشته بشه منظور چیه؟
۰
ارسال: #۵
RE: Learn Engineering Mathematics concepts
حتما با ۴ فرمول زیر آشنایی دارید :
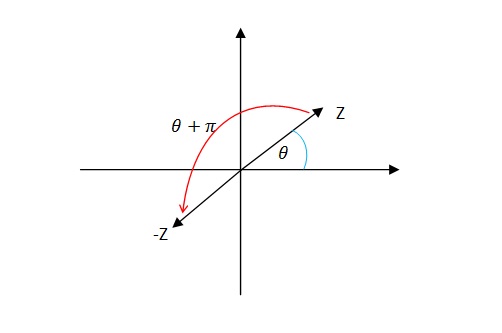
[tex]\large \bar{z}=re^{-i\Theta }[/tex]
[tex]\large -z=re^{i\(\Theta \Pi )}[/tex]
[tex]\large iz=re^{i\(\Theta \frac{\Pi}{2} )}[/tex]
[tex]\large -iz=re^{i\(\Theta -\frac{\Pi}{2} )}[/tex]
برای فهم این ۴ فرمول به شکل توجه کنید ، در شکل من یک z دلخواه رو رسم کردم؛ اگر بخوام z- رو رسم کنم دقیقا به اندازه [tex]\large \Theta \Pi[/tex] دوران داریم ، همین مثال رو می توان برای بقیه بسط داد :[tex]\large -z=re^{i\(\Theta \Pi )}[/tex]
[tex]\large iz=re^{i\(\Theta \frac{\Pi}{2} )}[/tex]
[tex]\large -iz=re^{i\(\Theta -\frac{\Pi}{2} )}[/tex]

۰
ارسال: #۶
RE: Learn Engineering Mathematics concepts
فرق Ln با ln :
[tex]y=Ln(z)=Ln® i\Theta[/tex]
[tex]y = ln(z)=ln® i(\Theta 2K\Pi )[/tex]
در ln کوچک ما یک ۲kpi هم داریم که کاربرد این در مکانیک هست که مثلا جواب رو در دور k می خوان بدست بیارن به این نحوه ln کوچک رو در نظر می گیرند.
[tex]y = ln(z)=ln® i(\Theta 2K\Pi )[/tex]
ارسال: #۷
سری فوریه
همان طور که می دونید رفتار تابع می تونه به ۲ صورت مورد بررسی قرار بگیره : ۱- رفتار منظم ۲- رفتار های نامنظم
توابع نا منظم رو نمیشه از طریق سری فوریه توصیف کرد اما اگر همون تابع در دامنه (+∞و-∞) انتگرال پذیر باشه می تونیم با استفاده از انتگرال فوریه Sin,Cos رفتار اون تابع رو به نحوی شبیه سازی کنیم ؛
[tex]\int_{0}^{\infty }(A(\omega )\cos \omega x b(\omega ) \sin \omega X)d\omega[/tex]
در سری فوریه هر چقدر [tex]\sum_{i=1}^{n}[/tex] بیشتر نوشته بشه همگرایی مشهود تر میشه
توابع نا منظم رو نمیشه از طریق سری فوریه توصیف کرد اما اگر همون تابع در دامنه (+∞و-∞) انتگرال پذیر باشه می تونیم با استفاده از انتگرال فوریه Sin,Cos رفتار اون تابع رو به نحوی شبیه سازی کنیم ؛
[tex]\int_{0}^{\infty }(A(\omega )\cos \omega x b(\omega ) \sin \omega X)d\omega[/tex]
در سری فوریه هر چقدر [tex]\sum_{i=1}^{n}[/tex] بیشتر نوشته بشه همگرایی مشهود تر میشه
۰
ارسال: #۸
Learn Engineering Mathematics concepts
دوست عزیز برای هر موضوع عنوانی مناسب خودش انتخاب کنید. توجه فرمایید:
مهمان عزیز شما قادر به مشاهده پیوندهای انجمن مانشت نمیباشید. جهت مشاهده پیوندها ثبت نام کنید.
بهتره موضوعات را جدا کنید. البته اینها مفاهیمی درش دیده نمیشه بیشتر یه سری نکته هست که بعضیش هم ظاهرا" درست نیستند .
ممنون میشم برای حفظ نظم انجمن اینکار را خودتان انجام بدین.یعنی هر موضوع را جدا کنید.
مهمان عزیز شما قادر به مشاهده پیوندهای انجمن مانشت نمیباشید. جهت مشاهده پیوندها ثبت نام کنید.
بهتره موضوعات را جدا کنید. البته اینها مفاهیمی درش دیده نمیشه بیشتر یه سری نکته هست که بعضیش هم ظاهرا" درست نیستند .
ممنون میشم برای حفظ نظم انجمن اینکار را خودتان انجام بدین.یعنی هر موضوع را جدا کنید.
۰
ارسال: #۹
Learn Engineering Mathematics concepts
هدف از زدن این تاپیک اینه که دوستان برند مطالعه کنند اون چیزی که فهمیدند رو اینجا بذارند شاید در این میان ایده ای* به نظرشون برسه عنوان هم نشون دهنده ی هدف تاپیک هست حالا الان باید چه کرد ؟
اونجاهایکه به نظرتون درست نمی رسه رو بگین خوشحال میشم .
ببینید ما دانشجو هستیم نه انبار حافظه ، اگر بریم هرچی تو کتاب کرویت سیگ رو نوشته اینجا paste کنیم که... (حیف ام اومد اینو نگم) به هر حال تو این تاپیک قرار نیست سوال کنکور حل بشه قراره مفاهیمی که می فهمیم رو اینجا قرار بدیم که متاسفانه علاقمند کم هست !
اونجاهایکه به نظرتون درست نمی رسه رو بگین خوشحال میشم .
ببینید ما دانشجو هستیم نه انبار حافظه ، اگر بریم هرچی تو کتاب کرویت سیگ رو نوشته اینجا paste کنیم که... (حیف ام اومد اینو نگم) به هر حال تو این تاپیک قرار نیست سوال کنکور حل بشه قراره مفاهیمی که می فهمیم رو اینجا قرار بدیم که متاسفانه علاقمند کم هست !
۰
ارسال: #۱۰
Learn Engineering Mathematics concepts
من نیت شما را میدونم و خوشحال میشم کمکتون کنم ولی ما خودمون را موظف کردیم که انجمن را مرتب کنیم تا قابل استفاده باشه. چون خواستید من بگم مواردی را عرض میکنم.
اولا" اون چیزایی که شما نوشتید مثالهایی از بعضی قسمتهای متغیرهای مختلط هست و مفاهیم نیستند. طبیعی است که یه مطلب بهتره کامل باشه. اگه یه مبحث را کامل نکات یا مفاهیمش را بگید خیلی بیشتر کمک میکنه تا از هر قسمت یه مثال ساده بزنید. البته مثال ساده هم اشکالی نداره فقط عنوان تاپیک فعلا" یه فاصله زیادی با محتوایش داره. بنابراین بنظرم در هر مورد یه تاپیک بزنید و عنوان با محتوا نزدیک باشه.
دوم اینکه نمیدونم چه ضرورتی هست عنوان را لاتین بزنید.
سوم اینکه ریاضیات مهمترین قسمتش دقتش هست. در مفاهیم و تعریفها. اگه این معیار رعایت نشه دیگه ریاضی نخواهد بود. مثلا" در پست شماره ۶ اومدین توابع را به رفتار منظم و غیر منظم تقسیم کردین. و از این دسته بندی برای سری فوریه و تبدیل فوریه استفاده کردین. خب این با مفاهیم علمی ریاضی و با تعاریف و مفاهیم تعریف شده خیلی فاصله داره. احتمالا" منظورتون از رفتار منظم ، متناوب بودن و متناوب نبودنه. حالا شرایط دیریکله برای وجود تبدیل فوریه را هم باز با این مفهوم در هم آمیختید. خب اینجوری که دیگه با علم ریاضی فاصله میگیرید و بنظرم نمیشه اینقدر وضوع را مختصر و بزبان عادی کرد. بعضی مفاهیم که شما بنام رفتار منظم تعریف کردین با مطالب مربوطه همخوانی نداره.
من تصورم اینه که شما میخواهید مطالب را روان بگید ولی روان گفتن با تغییر مفاهیم یا استفاده از اصطلاحات دگری که بعضی وقتها معانی دیگری میدن( بخصوص در ریاضی که بسیار باید دقیق باشیم )فاصله زیادی داره.
باز هم ازتون عذر میخوام و حاضرم اگه کاری از دستم برمیاد کمک کنم.
اولا" اون چیزایی که شما نوشتید مثالهایی از بعضی قسمتهای متغیرهای مختلط هست و مفاهیم نیستند. طبیعی است که یه مطلب بهتره کامل باشه. اگه یه مبحث را کامل نکات یا مفاهیمش را بگید خیلی بیشتر کمک میکنه تا از هر قسمت یه مثال ساده بزنید. البته مثال ساده هم اشکالی نداره فقط عنوان تاپیک فعلا" یه فاصله زیادی با محتوایش داره. بنابراین بنظرم در هر مورد یه تاپیک بزنید و عنوان با محتوا نزدیک باشه.
دوم اینکه نمیدونم چه ضرورتی هست عنوان را لاتین بزنید.
سوم اینکه ریاضیات مهمترین قسمتش دقتش هست. در مفاهیم و تعریفها. اگه این معیار رعایت نشه دیگه ریاضی نخواهد بود. مثلا" در پست شماره ۶ اومدین توابع را به رفتار منظم و غیر منظم تقسیم کردین. و از این دسته بندی برای سری فوریه و تبدیل فوریه استفاده کردین. خب این با مفاهیم علمی ریاضی و با تعاریف و مفاهیم تعریف شده خیلی فاصله داره. احتمالا" منظورتون از رفتار منظم ، متناوب بودن و متناوب نبودنه. حالا شرایط دیریکله برای وجود تبدیل فوریه را هم باز با این مفهوم در هم آمیختید. خب اینجوری که دیگه با علم ریاضی فاصله میگیرید و بنظرم نمیشه اینقدر وضوع را مختصر و بزبان عادی کرد. بعضی مفاهیم که شما بنام رفتار منظم تعریف کردین با مطالب مربوطه همخوانی نداره.
من تصورم اینه که شما میخواهید مطالب را روان بگید ولی روان گفتن با تغییر مفاهیم یا استفاده از اصطلاحات دگری که بعضی وقتها معانی دیگری میدن( بخصوص در ریاضی که بسیار باید دقیق باشیم )فاصله زیادی داره.
باز هم ازتون عذر میخوام و حاضرم اگه کاری از دستم برمیاد کمک کنم.
۰
ارسال: #۱۱
Learn Engineering Mathematics concepts
در مورد این تاپیک قبلا" صحبت شده و اشکالات گوشزد شده. بنظرم بدون توجه به پستها بهتره موضوعی را دوباره مطرح نکنیم که قبلا" بحث شده. واسه همین تاپیک بسته میشه.
Can I see some ID?
Feeling left out?
نگران نباش، فقط روی این لینک برای ثبت نام کلیک کن. رمزت رو فراموش کردی؟ اینجا به یادت میاریم! close

