۰
subtitle
ارسال: #۱
ساختمان داده-مرتبه زمانی صفحه ۱۵ کتاب پوران
سلام دوستان
میشه این سوال ها رو با راه حل،حلشون کنید؟
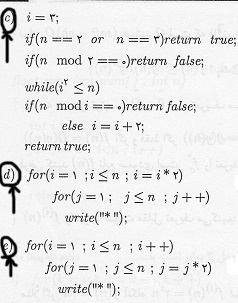
میشه این سوال ها رو با راه حل،حلشون کنید؟
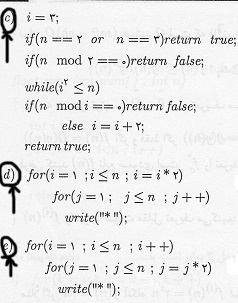
۱
ارسال: #۲
RE: ساختمان داده-مرتبه زمانی صفحه ۱۵ کتاب پوران
(۰۸ آبان ۱۳۹۵ ۱۲:۱۷ ب.ظ)Flora نوشته شده توسط: سلام دوستان
میشه این سوال ها رو با راه حل،حلشون کنید؟
سلام
در اولی، اون حالتهای خاص که در نظر گرفته نمیشوند. اصلش حلقه هست. در حلقه هم ممکن هست همون اولش، یعنی به ازای i=3، باقیموندهی n به i صفر بشه، مثلاً n=90000000 باشه. ولی باز بدترین حالت باید در نظر گرفت بشه. برای اینکه [tex]i^2<n[/tex] باشه، i باید [tex]\sqrt{n}[/tex] تا جلو بره. البته چون اینجا i = i + 2 میشه، باید [tex]\frac{\sqrt{n}}{2}[/tex] جلو بره که مهم نیست و مرتبهشون همون [tex]\theta(\sqrt{n})[/tex] هست. دقیقترش میشه [tex]\frac{\sqrt{n}}{2}-3[/tex] چون اولش از ۳ شروع میشه (و ۳ گام رفته جلو).
دومی هم باز راحت هست چون حلقهی داخلی، مستقل از حلقهی بیرونی هست. یعنی j هر بار تا n میره (به جای اینکه مثلاً تا i بره که نیاز به سیگما یا روشهای دیگه باشه). متغیر i هر بار ضربدر ۲ میشه تا وقتی که به n برسه، پس میشه [tex]\log(n)[/tex] بار. j هم که هر بار از ۱ تا n میره، پس مرتبهی کلی میشه [tex]n\cdot\log(n)[/tex]. اگر متغیر حلقهی داخلی به متغیر حلقهی بیرونی ربط داشت (مثلا j هر بار تا i میرفت) نمیشد به این راحتی ضرب کرد و باید از سیگما استفاده بشه مثلاً.
در سومی هم متغیر حلقهها مستقل هستند، اولی n تا گام داره و دومی [tex]\log(n)[/tex] تا. یعنی به ازای هر i، دومی [tex]\log(n)[/tex] تا دستور اجرا میکنه. بنابراین مرتبه مثل بالایی میشه [tex]n\cdot\log(n)[/tex]
۰
ارسال: #۳
RE: ساختمان داده-مرتبه زمانی صفحه ۱۵ کتاب پوران
ممنون.
ببخشید حلقه اول رو میشه بیشتر توضیح بدین؟
چرا میشه از مرتبه [tex]\sqrt{n}[/tex]
ببخشید حلقه اول رو میشه بیشتر توضیح بدین؟
چرا میشه از مرتبه [tex]\sqrt{n}[/tex]
ارسال: #۴
RE: ساختمان داده-مرتبه زمانی صفحه ۱۵ کتاب پوران
(۰۸ آبان ۱۳۹۵ ۰۱:۳۱ ب.ظ)Flora نوشته شده توسط: ممنون.خواهش میکنم.
ببخشید حلقه اول رو میشه بیشتر توضیح بدین؟
چرا میشه از مرتبه [tex]\sqrt{n}[/tex]
i از ۳ شروع میشه. اگه از اون دو تا دستور صرف نظر کنیم و بدترین حالت رو در نظر بگیریم که تا زمانی که [tex]i^2[/tex] از n کوچیکتر هست حداقل اون دو تا دستور اول اجرا نشه. یعنی حلقه ی while رو بررسی میکنیم.
اولش i=3
[tex]i^2<n[/tex] فرض میکنیم که else اجرا بشه تا حد امکان. (باز بدترین حالت رو در نظر میگیریم، دقت بشه توی سوالات باید به نکات دیگه ای هم توجه کنیم گاهاََ)
i+=2 پس i میشه ۵
حالا ۲۵ رو با n مقایسه میکنه.
دفعه ی بعد i=7 و ۴۹ با n مقایسه میشه.
یعنی هر بار [tex](3+2k)^2[/tex] با n مقایسه میشه.
دفعه ی اول [tex]i^2=(3+2\cdot1)^2[/tex]
دفعه ی دوم [tex]i^2=(3+2\cdot2)^2[/tex]
دفعه ی سوم [tex]i^2=(3+2\cdot3)^2[/tex]
.
.
دفعه ی k ام [tex]i^2=(3+2\cdot k)^2[/tex]
تا زمانی که [tex]i^2<=n[/tex]
یعنی باید k رو به دست بیاریم. رابطه رو داریم که بعد از k بار چه اتفاقی میفته. حالا اون مقدار[tex]i^2=(3+2\cdot k)^2[/tex] باید کوچیکتر مساوی n باشه دیگه.
k میشه:
[tex]i^2=(3+2k)^2<=\: n\: \: \: \: \longrightarrow\: \: \: 9+4k^2+12k\: =\theta(k^2)<=\: n\: \: \longrightarrow\: k<=\sqrt{n}[/tex]
ارسال: #۵
RE: ساختمان داده-مرتبه زمانی صفحه ۱۵ کتاب پوران
(۰۸ آبان ۱۳۹۵ ۰۷:۰۹ ب.ظ)Pure Liveliness نوشته شده توسط:عالی بود.(08 آبان ۱۳۹۵ ۰۱:۳۱ ب.ظ)Flora نوشته شده توسط: ممنون.خواهش میکنم.
ببخشید حلقه اول رو میشه بیشتر توضیح بدین؟
چرا میشه از مرتبه [tex]\sqrt{n}[/tex]
i از ۳ شروع میشه. اگه از اون دو تا دستور صرف نظر کنیم و بدترین حالت رو در نظر بگیریم که تا زمانی که [tex]i^2[/tex] از n کوچیکتر هست حداقل اون دو تا دستور اول اجرا نشه. یعنی حلقه ی while رو بررسی میکنیم.
اولش i=3
...
خییییلی ممنونم.
Pure Liveliness، در تاریخ ۰۸ آبان ۱۳۹۵ ۱۰:۱۰ ب.ظ برای این مطلب یک پانوشت گذاشته است:
خواهش میکنم 
Can I see some ID?
Feeling left out?
نگران نباش، فقط روی این لینک برای ثبت نام کلیک کن. رمزت رو فراموش کردی؟ اینجا به یادت میاریم! close


