۰
subtitle
ارسال: #۱
مشکل در حل تست سال ۸۴ مهندسی کامپیوتر ( مبحث مجموعه های تفاضل متفارن )
![[تصویر: 423506_bsq5_20161004_150342.jpg]](https://img.manesht.ir/423506_bsq5_20161004_150342.jpg)
من جوابشو تو کتاب پوران دیدم ولی اصلن یکلمه توضیح نداده نفهمیدم چی به چیه لطفا واضح توضیح بدین ممنون میشم
۱
ارسال: #۲
RE: مشکل در حل تست سال ۸۴ مهندسی کامپیوتر ( مبحث مجموعه های تفاضل متفارن )
(۱۳ مهر ۱۳۹۵ ۰۴:۰۸ ب.ظ)jionelmessi نوشته شده توسط:سلام.من به کتاب پوران دسترسی ندارم که ببینم چطور پاسخ دادن.ولی مطمئنا که سوالتون ناقصه.چرا که برای حل این سوال نیازه بدونیم که چند عضو به هر سه مجموعه A و B و C تعلق دارند!
من جوابشو تو کتاب پوران دیدم ولی اصلن یکلمه توضیح نداده نفهمیدم چی به چیه لطفا واضح توضیح بدین ممنون میشم
حال اگه من بیام این مجهول رو x قرار بدم.(یعنی x عضو به هر سه مجموعه A و B و C تعلق داشته باشد)،نمودار ون سوال به صورت زیر میشه:
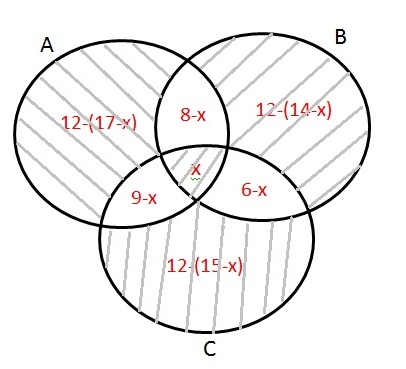
در نتیجه جواب برابر جاهایی میشه که هاشور خوردند:
[tex]x\: +\: (12-(17-x))\: +\: (12-(14-x))\: +\: (12-(15-x))[/tex]
[tex]=\: x\: +\: (x-5)\: +\: (x-2)\: +\: (x-3)[/tex]
[tex]=\: 4x\: -\: 10[/tex]
[tex]=\: x\: +\: (x-5)\: +\: (x-2)\: +\: (x-3)[/tex]
[tex]=\: 4x\: -\: 10[/tex]
-----------------------
حال دیگه بستگی داره که x(تعداد اعضای [tex]A\: \cap\: B\: \cap\: C[/tex] ) چند باشه؟
بایستی مقدار x طوری باشه که تعداد اعضای هیچکدوم از نواحی منفی نباشه!که تنها با x برابر ۵ و ۶ این شرط برقراره!
اگر x=5 باشه،جواب سوال برابر [tex]4x-10\: = 4\: (5)\: -\: 10\: =\: 10[/tex] میشه! که تو هیچکدوم از گزینه ها نیست!
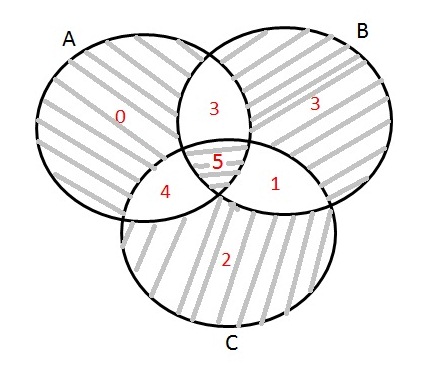
اگر x=6 باشه،جواب سوال برابر [tex]4x-10\: = 4\: (6)\: -\: 10\: =\: 14[/tex] میشه!که بازم تو هیچکدوم از گزینه ها نیست!
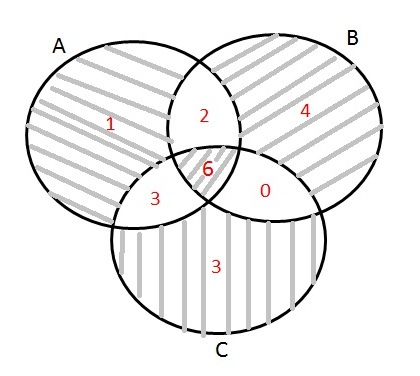
در هر صورت هیچکدوم از گزینه ها جواب سوال نیست.
۱
ارسال: #۳
RE: مشکل در حل تست سال ۸۴ مهندسی کامپیوتر ( مبحث مجموعه های تفاضل متفارن )
من طبق توضیحی که دکتر اجلالی توی کتاب جامع نصیر دادند، حلش رو مینویسم:
یه نمودار وِن می کشیم و به صورت زیر محل های اشتراک و غیر اشتراک بین سه مجموعه رو نام گذاری می کنیم.
اشتراک هر سه مجموعه ی A و B و C: ناحیه ی f7
اشتراک دو مجموعه ی A و B : ناحیه ی f5
اشتراک دو مجموعه ی A و C : ناحیه ی f4
اشتراک دو مجموعه ی B و C : ناحیه ی f6
ناحیه ای از A که با دو مجموعه ی دیگر تلاقی ندارد: ناحیه ی f1
ناحیه ای از B که با دو مجموعه ی دیگر تلاقی ندارد: ناحیه ی f2
ناحیه ای از C که با دو مجموعه ی دیگر تلاقی ندارد: ناحیه ی f3
حالا فرضیاتی که توی مساله داده شده رو مینویسیم:
۱: [tex]|A|=12\: \longrightarrow\: |f1|+|f4|+|f5|+|f7|=12[/tex]
۲: [tex]|B|=12\: \longrightarrow\: |f2|+|f5|+|f6|+|f7|=12[/tex]
۳: [tex]|C|=12\: \longrightarrow\: |f3|+|f4|+|f6|+|f7|=12[/tex]
۴: [tex]|A\cap B|=8\: \longrightarrow\: |f5|+|f7|=8[/tex]
۵: [tex]|A\cap C|=9\: \longrightarrow\: |f4|+|f7|=9[/tex]
۶: [tex]|B\cap C|=6\: \longrightarrow\: |f6|+|f7|=6[/tex]
۷: [tex]|A\cap B\cap C|=5\: \longrightarrow\: |f7|=5[/tex]
خب حالا کار خیلی ساده تر میشه، چون با استفاده از این روابط می تونیم همه ی [tex]fi[/tex] ها رو به دست بیاریم.
۸: با استفاده از رابطه ی ۶ و ۷ : [tex]|f6|=1[/tex]
۹: با استفاده از رابطه ی ۵ و ۷ : [tex]|f4|=4[/tex]
۱۰: با استفاده از رابطه ی ۴ و ۷ : [tex]|f5|=3[/tex]
۱۱: با استفاده از رابطه ی ۸و ۱۰و ۷و ۳ : [tex]|f3|=2[/tex]
۱۲: با استفاده از رابطه ی ۸ و ۱۰ و ۷ و ۲ : [tex]|f2|=3[/tex]
۱۳: با استفاده از رابطه ی ۱و ۷و ۹ و ۱۰ : [tex]|f1|=0[/tex]
خب حالا صورت سوال معادل میشه با [tex]|f1|+|f2|+|f3|+|f7|[/tex] چرا؟
[tex]|A \bigtriangleup B \bigtriangleup C|=\{x|\: x\in A\: xor\: x\in B\: xor\: x\in C\}[/tex] که حاصلش برابر هست با ۱۰
یه نمودار وِن می کشیم و به صورت زیر محل های اشتراک و غیر اشتراک بین سه مجموعه رو نام گذاری می کنیم.
اشتراک هر سه مجموعه ی A و B و C: ناحیه ی f7
اشتراک دو مجموعه ی A و B : ناحیه ی f5
اشتراک دو مجموعه ی A و C : ناحیه ی f4
اشتراک دو مجموعه ی B و C : ناحیه ی f6
ناحیه ای از A که با دو مجموعه ی دیگر تلاقی ندارد: ناحیه ی f1
ناحیه ای از B که با دو مجموعه ی دیگر تلاقی ندارد: ناحیه ی f2
ناحیه ای از C که با دو مجموعه ی دیگر تلاقی ندارد: ناحیه ی f3
حالا فرضیاتی که توی مساله داده شده رو مینویسیم:
۱: [tex]|A|=12\: \longrightarrow\: |f1|+|f4|+|f5|+|f7|=12[/tex]
۲: [tex]|B|=12\: \longrightarrow\: |f2|+|f5|+|f6|+|f7|=12[/tex]
۳: [tex]|C|=12\: \longrightarrow\: |f3|+|f4|+|f6|+|f7|=12[/tex]
۴: [tex]|A\cap B|=8\: \longrightarrow\: |f5|+|f7|=8[/tex]
۵: [tex]|A\cap C|=9\: \longrightarrow\: |f4|+|f7|=9[/tex]
۶: [tex]|B\cap C|=6\: \longrightarrow\: |f6|+|f7|=6[/tex]
۷: [tex]|A\cap B\cap C|=5\: \longrightarrow\: |f7|=5[/tex]
خب حالا کار خیلی ساده تر میشه، چون با استفاده از این روابط می تونیم همه ی [tex]fi[/tex] ها رو به دست بیاریم.
۸: با استفاده از رابطه ی ۶ و ۷ : [tex]|f6|=1[/tex]
۹: با استفاده از رابطه ی ۵ و ۷ : [tex]|f4|=4[/tex]
۱۰: با استفاده از رابطه ی ۴ و ۷ : [tex]|f5|=3[/tex]
۱۱: با استفاده از رابطه ی ۸و ۱۰و ۷و ۳ : [tex]|f3|=2[/tex]
۱۲: با استفاده از رابطه ی ۸ و ۱۰ و ۷ و ۲ : [tex]|f2|=3[/tex]
۱۳: با استفاده از رابطه ی ۱و ۷و ۹ و ۱۰ : [tex]|f1|=0[/tex]
خب حالا صورت سوال معادل میشه با [tex]|f1|+|f2|+|f3|+|f7|[/tex] چرا؟
[tex]|A \bigtriangleup B \bigtriangleup C|=\{x|\: x\in A\: xor\: x\in B\: xor\: x\in C\}[/tex] که حاصلش برابر هست با ۱۰
Can I see some ID?
Feeling left out?
نگران نباش، فقط روی این لینک برای ثبت نام کلیک کن. رمزت رو فراموش کردی؟ اینجا به یادت میاریم! close


