۰
subtitle
ارسال: #۱
جایگذاری - جزوه دکتر یوسفی
جلسه سوم، صفحه ۳ (ادامهش هم صفحه بعدش هست!)
از اونجا که فاکتور گرفته به بعد رو توضیح بدید لطفاً.
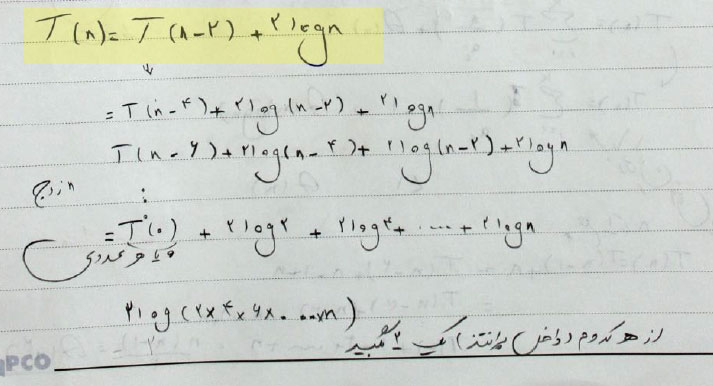

مهمان عزیز شما قادر به مشاهده پیوندهای انجمن مانشت نمیباشید. جهت مشاهده پیوندها ثبت نام کنید.
از اونجا که فاکتور گرفته به بعد رو توضیح بدید لطفاً.
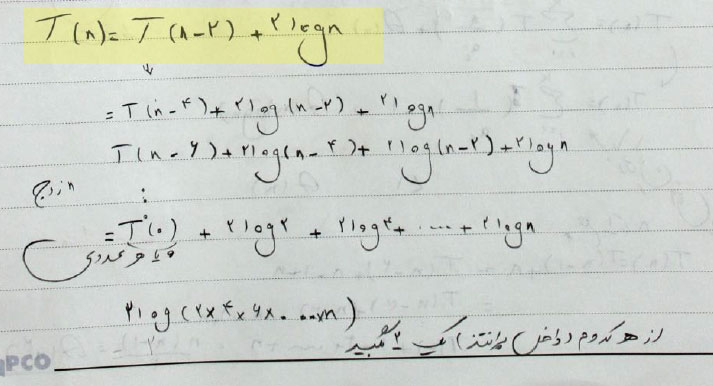

مهمان عزیز شما قادر به مشاهده پیوندهای انجمن مانشت نمیباشید. جهت مشاهده پیوندها ثبت نام کنید.
۰
ارسال: #۲
RE: جایگذاری - جزوه دکتر یوسفی
[tex]2\log(2\ast4\ast6\ast...\ast n)=[/tex]
[tex]2\log((1\ast2).(2\ast2).(3\ast2)...(\frac{n}{2}\ast2))=2\log(2^{\frac{n}{2}}\ast(\frac{n}{2})!)=[/tex]
[tex] 2\log2^{\frac{n}{2}} 2\log(\frac{n}{2}!)=[/tex]
[tex] ^{ }n 2\frac{n}{2}\log\frac{n}{2}=[/tex]
[tex] n nlog\frac{n}{2}= ^{ }n(l \log\frac{n}{2})=[/tex]
[tex]n(\log2 \log\frac{n}{2})= n(\log(2\ast\frac{n}{2}))=nlogn[/tex]
یه نکته که داره اینه !logn تقریبا برابر nlogn هست
[tex]2\log((1\ast2).(2\ast2).(3\ast2)...(\frac{n}{2}\ast2))=2\log(2^{\frac{n}{2}}\ast(\frac{n}{2})!)=[/tex]
[tex] 2\log2^{\frac{n}{2}} 2\log(\frac{n}{2}!)=[/tex]
[tex] ^{ }n 2\frac{n}{2}\log\frac{n}{2}=[/tex]
[tex] n nlog\frac{n}{2}= ^{ }n(l \log\frac{n}{2})=[/tex]
[tex]n(\log2 \log\frac{n}{2})= n(\log(2\ast\frac{n}{2}))=nlogn[/tex]
یه نکته که داره اینه !logn تقریبا برابر nlogn هست
۰
ارسال: #۳
RE: جایگذاری - جزوه دکتر یوسفی
(۲۰ مهر ۱۳۹۳ ۱۱:۱۵ ب.ظ)Ametrine نوشته شده توسط: جلسه سوم، صفحه ۳ (ادامهش هم صفحه بعدش هست!)
از اونجا که فاکتور گرفته به بعد رو توضیح بدید لطفاً.
مهمان عزیز شما قادر به مشاهده پیوندهای انجمن مانشت نمیباشید. جهت مشاهده پیوندها ثبت نام کنید.
خب، تا اونجا که بسط دادنو گفتم یادتونه؟
ما اومدیم عبارته مقابل T(n رو هربار بسط دادیم، انقدر که بشه [tex]T(n)=T(0) A[/tex]
حالا اون A چی هست؟ [tex]A=2\log2 2\log4 2\log6 ...... 2\log n[/tex]
از همشون یه ۲ فاکتور میگیریم و میدونیم طبق خاصیت لگاریتم [tex]\log a \log b=\log a\cdot b[/tex] پس عبارتمون تبدیل میشه به [tex]A=2\log(2\cdot4\cdot8....\cdot n)[/tex] و حالا باز از داخل لگاریتم از هرکدوم یه ۲ گرفتیم( چون میخوایم اعداد به ترتیب شن و وقتی یه ۲ بگیریم به ترتیب میشن، اینم میدونیم که تعداد اعداد زوج ۲ تا n به اندازه n/2 تاست. پس میشه [tex]A=2\log(2^{\frac{n}{2}}\cdot1\cdot2\cdot3\cdot4\cdot5.....\cdot\frac{n}{2})َ[/tex]
حالا دوباره لگاریتمو به جمع دو لگاریتم تبدیل میکنیم[tex]A=2(\log2^{\frac{n}{2}} \log\: \frac{n}{2}!)َ[/tex]
در نهایت هم میگیم که A تقریبا معادل [tex]A=2(\frac{n}{2} \frac{n}{2}\log\: \frac{n}{2})َ[/tex] میشود
ارسال: #۴
RE: جایگذاری - جزوه دکتر یوسفی
(۲۱ مهر ۱۳۹۳ ۱۲:۱۲ ق.ظ)Ava.arshad94 نوشته شده توسط: خب، تا اونجا که بسط دادنو گفتم یادتونه؟تشکر از Donna و Ava
ما اومدیم عبارته مقابل T(n رو هربار بسط دادیم، انقدر که بشه [tex]T(n)=T(0) A[/tex]
حالا اون A چی هست؟ [tex]A=2\log2 2\log4 2\log6 ...... 2\log n[/tex]
از همشون یه ۲ فاکتور میگیریم و میدونیم طبق خاصیت لگاریتم [tex]\log a \log b=\log a\cdot b[/tex] پس عبارتمون تبدیل میشه به [tex]A=2\log(2\cdot4\cdot8....\cdot n)[/tex] و حالا باز از داخل لگاریتم از هرکدوم یه ۲ گرفتیم( چون میخوایم اعداد به ترتیب شن و وقتی یه ۲ بگیریم به ترتیب میشن، اینم میدونیم که تعداد اعداد زوج ۲ تا n به اندازه n/2 تاست. پس میشه [tex]A=2\log(2^{\frac{n}{2}}\cdot1\cdot2\cdot3\cdot4\cdot5.....\cdot\frac{n}{2})َ[/tex]
حالا دوباره لگاریتمو به جمع دو لگاریتم تبدیل میکنیم[tex]A=2(\log2^{\frac{n}{2}} \log\: \frac{n}{2}!)َ[/tex]
در نهایت هم میگیم که A تقریبا معادل [tex]A=2(\frac{n}{2} \frac{n}{2}\log\: \frac{n}{2})َ[/tex] میشود
فقط تشخیص این ریتمه یه کم سخته.

(صرفاً تو این سوال منظورم نیست، کلی میگم.)
فکر کنم تنها راه حل تمرین زیاد باشه.
Can I see some ID?
Feeling left out?
نگران نباش، فقط روی این لینک برای ثبت نام کلیک کن. رمزت رو فراموش کردی؟ اینجا به یادت میاریم! close


