۰
subtitle
ارسال: #۱
ترتیب ادغــــــــــــــــــــــــام!!
سلام !
میتونید جواب این سوال رو به من بگید یا حداقل راهنماییم کنید؟
چار فایل مرتب شده ی f اندیس ۱ و fاندیس ۲ و fاندیس ۳وf اندیس ۴به ترتیب با اندازه های ۵۰و۱۰۰و۲۰۰و۳۰۰ در اختیار داریم.
ترتیب ادغام دو به دوی آن ها چگونه باشد که کمترین مقدار مقایسه ها صورت بگیرد!؟
استاد میگف یه جورایی ربط داره به مبحث "هافمن" از درس طراحی الگوریتم!
میتونید جواب این سوال رو به من بگید یا حداقل راهنماییم کنید؟
چار فایل مرتب شده ی f اندیس ۱ و fاندیس ۲ و fاندیس ۳وf اندیس ۴به ترتیب با اندازه های ۵۰و۱۰۰و۲۰۰و۳۰۰ در اختیار داریم.
ترتیب ادغام دو به دوی آن ها چگونه باشد که کمترین مقدار مقایسه ها صورت بگیرد!؟
استاد میگف یه جورایی ربط داره به مبحث "هافمن" از درس طراحی الگوریتم!
۰
ارسال: #۲
ترتیب ادغــــــــــــــــــــــــام!!
نمیشه دقیقا گفت مربوط به مبحث هافمنه راه حلش شبیه به الگوریتم هافمنه !
جوابش اینجوری میشه که اول ۵۰ با ۱۰۰ ادغام میشه که تعداد ۱۵۰ مقایسه لازم داره . ۲۰۰ با ۱۵۰ ادغام میشه که ۳۵۰ مقایسه لازم داره . ۳۰۰ با ۳۵۰ ادغام میشه که ۶۵۰ مقایسه لازم داره و در نهایت تعداد کل مقایسه ها برابر با ۱۱۵۰=۱۵۰+۳۵۰+۶۵۰ میشه .
شبیه بودنش به الگوریتم هافمن اینجاست که می تونی برای حل کردنش از درخت دودویی استفاده کنی که پیاده سازی این درخت دقیقا مثل درخت هافمنه (دو مقدار کوچکتر رو از لیست برداشته و با هم ادغام می کنیم ) اسمش هم درخت دودویی ادغامه. به این صورت که گره های خارجی (برگ ها) معرف فایل ها هستند و گره های داخلی معرف فایلی است که از ادغام دو فایل نشان داده شده توسط فرزندانش حاصل شده است و عدد داخل هر گره اندازه فایل نمایش داده شده توسط آن گره است .
برای محاسبه ی تعداد مقایسه ها در حالت کلی هم اگر [tex]d_{i}[/tex] برابر مسافت فایل [tex]F_{i}[/tex] در درخت دودویی ادغام باشد(فاصله از ریشه ) و [tex]q_{i}[/tex] اندازه فایل [tex]F_{i}[/tex] (تعداد رکورد هاش) باشد ، تعداد کل رکورد های جابجا شده از این رابطه بدست میاد
[tex]\sum _{i=0}^{n} d_{i} q_{i}[/tex]
که اگه توی این سوال درخت دودویی ادغام رو رسم بکنی جواب اینجوری بدست میاد
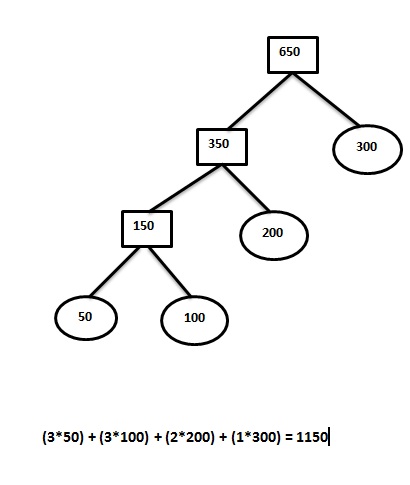
(۳*۵۰)+(۳*۱۰۰)+(۲*۲۰۰)+(۱*۳۰۰)=۱۱۵۰
جوابش اینجوری میشه که اول ۵۰ با ۱۰۰ ادغام میشه که تعداد ۱۵۰ مقایسه لازم داره . ۲۰۰ با ۱۵۰ ادغام میشه که ۳۵۰ مقایسه لازم داره . ۳۰۰ با ۳۵۰ ادغام میشه که ۶۵۰ مقایسه لازم داره و در نهایت تعداد کل مقایسه ها برابر با ۱۱۵۰=۱۵۰+۳۵۰+۶۵۰ میشه .
شبیه بودنش به الگوریتم هافمن اینجاست که می تونی برای حل کردنش از درخت دودویی استفاده کنی که پیاده سازی این درخت دقیقا مثل درخت هافمنه (دو مقدار کوچکتر رو از لیست برداشته و با هم ادغام می کنیم ) اسمش هم درخت دودویی ادغامه. به این صورت که گره های خارجی (برگ ها) معرف فایل ها هستند و گره های داخلی معرف فایلی است که از ادغام دو فایل نشان داده شده توسط فرزندانش حاصل شده است و عدد داخل هر گره اندازه فایل نمایش داده شده توسط آن گره است .
برای محاسبه ی تعداد مقایسه ها در حالت کلی هم اگر [tex]d_{i}[/tex] برابر مسافت فایل [tex]F_{i}[/tex] در درخت دودویی ادغام باشد(فاصله از ریشه ) و [tex]q_{i}[/tex] اندازه فایل [tex]F_{i}[/tex] (تعداد رکورد هاش) باشد ، تعداد کل رکورد های جابجا شده از این رابطه بدست میاد
[tex]\sum _{i=0}^{n} d_{i} q_{i}[/tex]
که اگه توی این سوال درخت دودویی ادغام رو رسم بکنی جواب اینجوری بدست میاد

(۳*۵۰)+(۳*۱۰۰)+(۲*۲۰۰)+(۱*۳۰۰)=۱۱۵۰
۰
Can I see some ID?
Feeling left out?
نگران نباش، فقط روی این لینک برای ثبت نام کلیک کن. رمزت رو فراموش کردی؟ اینجا به یادت میاریم! close

