۰
subtitle
ارسال: #۱
سوال از دو نکته موجود در فصل ۱ کتاب طورانی
این یکی از نکات کتاب آمارو احتمال طورانیه، اما من متوجه نمیشم منطق جوابشو که چطور به این فرمول رسیده:
به نظرم اشتباهه (سمت راست با چپ تطابق ندارن)
تو چاپ قبلی معادل عبارت سمت چپ در سمت راست نوشته شده بود اما تو چاپ جدید مشخص نیست کدوم درسته؟
به نظرم حتما باید با شرط k>=n حل بشه .....
۱) تعداد تقسیمات n شی متمایز در k سلول به طوریکه در هر سلول حداکثر یک شی قرار گیرد.
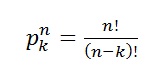
۲) مساله انطباق(جورها)
• اگر کسی منطق این فرمولارو و اثباتشو میدونه، لطف کنه بذاره ممنون میشم.
اگر سه حرف a , b , c مفروض باشند، به ترتیب قرار گرفتن آنها به طوریکه هیچ یک در جایگاه فعلیشان قرار نگیرند، ترتیب ناسازگار میگویند.
۱) تعداد ترتیب های ناسازگار n شی متمایز:
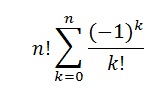
۲) تعداد ترتیب های ناسازگار r شی ازn شی متمایز:
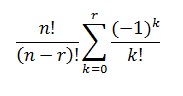
به نظرم اشتباهه (سمت راست با چپ تطابق ندارن)
تو چاپ قبلی معادل عبارت سمت چپ در سمت راست نوشته شده بود اما تو چاپ جدید مشخص نیست کدوم درسته؟
به نظرم حتما باید با شرط k>=n حل بشه .....
۱) تعداد تقسیمات n شی متمایز در k سلول به طوریکه در هر سلول حداکثر یک شی قرار گیرد.
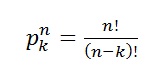
۲) مساله انطباق(جورها)
• اگر کسی منطق این فرمولارو و اثباتشو میدونه، لطف کنه بذاره ممنون میشم.
اگر سه حرف a , b , c مفروض باشند، به ترتیب قرار گرفتن آنها به طوریکه هیچ یک در جایگاه فعلیشان قرار نگیرند، ترتیب ناسازگار میگویند.
۱) تعداد ترتیب های ناسازگار n شی متمایز:
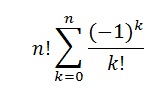
۲) تعداد ترتیب های ناسازگار r شی ازn شی متمایز:
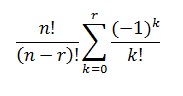
۰
ارسال: #۲
RE: سوال از دو نکته موجود در فصل ۱ کتاب طورانی
برای اثبات فرمول تعداد ترتیب های ناسازگار n شی متمایز میشه از اصل شمول و عدم شمول استفاده کرد.به صورت زیر اثبات میشه:
فرض کنید که [tex]B_{i}[/tex] رو مجموعه ترتیب هایی در نظر بگیریم که شی i در جای طبیعی خودش قرار گرفته.در واقع حالا ما باید تعداد اعضای مجموعه [tex]|\bar{B}_{1}.\bar{B}_{2}.\bar{B}_{3}...\bar{B}_{n}|[/tex] رو به دست بیاریم که همون تعداد ترتیب هایی میشه که هیچ کدام از این n تا شی سر جای خودشون نیستن.
فرض کنید که [tex]B_{i}[/tex] رو مجموعه ترتیب هایی در نظر بگیریم که شی i در جای طبیعی خودش قرار گرفته.در واقع حالا ما باید تعداد اعضای مجموعه [tex]|\bar{B}_{1}.\bar{B}_{2}.\bar{B}_{3}...\bar{B}_{n}|[/tex] رو به دست بیاریم که همون تعداد ترتیب هایی میشه که هیچ کدام از این n تا شی سر جای خودشون نیستن.
[tex]|\bar{B}_{1}.\bar{B}_{2}.\bar{B}_{3}...\bar{B}_{n}|=|U|-\sum |B_{i}| \sum |B_{i}.B_{j}|-...(-1)^{n}|B_{1}.B_{2}...B_{n}|=n!-\binom{n}{1}(n-1)! \binom{n}{2}(n-2)!-...(-1)^{n}\binom{n}{n}(n-n)!=\frac{n!}{0!}-\frac{n!}{1!} \frac{n!}{2!}-...-(-1)^{n}\frac{n!}{n!}=n!(\frac{1}{0!} \frac{1}{1!}-\frac{1}{2!}-...\frac{(-1)^{n}}{n!})=n!\sum_{i=0}^{n}\frac{(-1)^{i}}{i!}[/tex]
Can I see some ID?
Feeling left out?
نگران نباش، فقط روی این لینک برای ثبت نام کلیک کن. رمزت رو فراموش کردی؟ اینجا به یادت میاریم! close
