۰
subtitle
ارسال: #۱
روابط بازگشتی - روش Akra-Bazi
سلام
ی همچین مسائلی که به روش Akra-Bazii حل شده رو نمیشه به روشی راحت تر حل نمود
روش دیگه ای پیشنهاد می کنید؟
۲T(n/4)+3T(n/6)+nlogn
ی همچین مسائلی که به روش Akra-Bazii حل شده رو نمیشه به روشی راحت تر حل نمود
روش دیگه ای پیشنهاد می کنید؟
۲T(n/4)+3T(n/6)+nlogn
۱
ارسال: #۲
RE: روابط بازگشتی - روش Akra-Bazi
سلام. وقت بخیر.
منم با جواب آقای Iranian Wizard موافقم. اگه بخام حل کنم هم همین درخت رو رسم میکنم. ولی وقتی رابطه به شکل [tex]T(n)=\sum a_iT(\frac{n}{b_i})+g(n)[/tex] باشه، وقتی شرط [tex]\sum \frac{a_i}{b_i}=1[/tex] برقرار باشه میگم رابطه مشابه با [tex]T(n)=2T(n/2)+g(n)[/tex] هست که اگه توان n در چندجملهای برابر ۱ باشه، رابطه بازگشتی از مرتبه [tex]\theta(g(n)\lg n)[/tex] میشه. تو شرایط حدی و اعشاری این رابطه رو چک نکردم ولی وقتی تعداد جملات محدوده و ضرایب اعداد طبیعی هستن جواب میده.
منم با جواب آقای Iranian Wizard موافقم. اگه بخام حل کنم هم همین درخت رو رسم میکنم. ولی وقتی رابطه به شکل [tex]T(n)=\sum a_iT(\frac{n}{b_i})+g(n)[/tex] باشه، وقتی شرط [tex]\sum \frac{a_i}{b_i}=1[/tex] برقرار باشه میگم رابطه مشابه با [tex]T(n)=2T(n/2)+g(n)[/tex] هست که اگه توان n در چندجملهای برابر ۱ باشه، رابطه بازگشتی از مرتبه [tex]\theta(g(n)\lg n)[/tex] میشه. تو شرایط حدی و اعشاری این رابطه رو چک نکردم ولی وقتی تعداد جملات محدوده و ضرایب اعداد طبیعی هستن جواب میده.
ارسال: #۳
RE: روابط بازگشتی - روش Akra-Bazi
(۱۰ مهر ۱۳۹۵ ۰۱:۰۲ ق.ظ)Jooybari نوشته شده توسط: سلام. وقت بخیر.
منم با جواب آقای Iranian Wizard موافقم. اگه بخام حل کنم هم همین درخت رو رسم میکنم. ولی وقتی رابطه به شکل [tex]T(n)=\sum a_iT(\frac{n}{b_i})+g(n)[/tex] باشه، وقتی شرط [tex]\sum \frac{a_i}{b_i}=1[/tex] برقرار باشه میگم رابطه از مرتبه [tex]\theta(g(n)\lg n)[/tex] میشه. تو شرایط حدی و اعشاری این رابطه رو چک نکردم ولی وقتی تعداد جملات محدوده و ضرایب اعداد طبیعی هستن جواب میده.
علت اینکه من قانع نشدم (البته چرا، برای [tex]O[/tex] بزرگ میشه از تقسیمات داخل لگاریتم چشمپوشی کرد، منتهی برای [tex]\theta[/tex] به این راحتی نمیشه گفت. درسته که در مثلاً ۳ سطر اول از درخت، عدد نسبتاً قابل صرفنظری از [tex]\log(n)[/tex] کم میشه ولی همیشه نمیشه صرف نظر کرد. مثلاً ممکن هست بعد از [tex]\log(n)[/tex] سطر، اون عددی که داخل رادیکال بهش تقسیم میشه، قابل مقایسه با [tex]n[/tex] باشه، در اون صورت جواب میشه [tex]\log(n)\cdot\log(n)[/tex]. الان حضور ذهن ندارم ولی مثالهایی دیدم که صرف نظر کردن از تقسیم داخل لگاریتم باعث میشه کران بیش از حد بالایی برای مرتبه به دست بیاد (اما برای O مشکلی نیست).
۰
ارسال: #۴
RE: روابط بازگشتی - روش Akra-Bazi
سلام.
میشه از روش حد رفت. می دونیم که [tex]T(\frac{n}{4})[/tex] از [tex]T(\frac{n}{6})[/tex] بزرگتر هست. خب پس : [tex]T(\frac{n}{6})<T(\frac{n}{4})[/tex] در نتیجه اگه جای [tex]T(\frac{n}{6})[/tex] بذاریم [tex]T(\frac{n}{4})[/tex] به این نتیجه می رسیم که:
[tex]T(n)=2T(\frac{n}{4})+3T(\frac{n}{6})+nlogn\: <\: 2T(\frac{n}{4})+3T(\frac{n}{4})+nlogn\: =5T(\frac{n}{4})+nlogn[/tex] که حالا این [tex]5T(\frac{n}{4})+nlogn[/tex] رو میشه از قضیه ی اصلی حلش کرد، که مرتبه ش میشه [tex]n^{\log_4^5}=n^{1+k}[/tex]
خب پس با توجه به رابطه ی بالا می دونیم که : [tex]T(n)\: <\: n^{1+k2}[/tex]
حالا با توجه به این که [tex]T(\frac{n}{6})[/tex] از [tex]T(\frac{n}{4})[/tex] کوچیکتره، اگه توی رابطه تووش بذاریم:
[tex]2T(\frac{n}{6})+3T(\frac{n}{6})=5T(\frac{n}{6})\: <T(n)=2T(\frac{n}{4})+3T(\frac{n}{6})+nlogn\: [/tex] که اگه مرتبه ی سمت چپ رو به دست بیاریم با قضیه ی اصلی که از [tex]T(n)[/tex] مرتبه ش کمتر هست میشه [tex]T(n)=\Omega(nlogn)[/tex]
پس : [tex]nlogn<T(n)<n^{1+k2}[/tex] این فقط حدودش رو داد و حد بالا و پایین یکی نیست که ازش به این نتیجه برسیم که مرتبه ی تابع همون میشه.
من با تغییر متغیر هم رفتم. منتها چون که مجبوریم یه جا جای ۶ عدد دیگه ای بذاریم جواب درست در نیومد.
این فقط حدودش هست و میشه باهاش گزینه حذف کرد. ظاهراََ باید از همون روش بمب اتم رفت. باز دوستانی که بلد هستند انشاالله راهنمایی میکنن.
میشه از روش حد رفت. می دونیم که [tex]T(\frac{n}{4})[/tex] از [tex]T(\frac{n}{6})[/tex] بزرگتر هست. خب پس : [tex]T(\frac{n}{6})<T(\frac{n}{4})[/tex] در نتیجه اگه جای [tex]T(\frac{n}{6})[/tex] بذاریم [tex]T(\frac{n}{4})[/tex] به این نتیجه می رسیم که:
[tex]T(n)=2T(\frac{n}{4})+3T(\frac{n}{6})+nlogn\: <\: 2T(\frac{n}{4})+3T(\frac{n}{4})+nlogn\: =5T(\frac{n}{4})+nlogn[/tex] که حالا این [tex]5T(\frac{n}{4})+nlogn[/tex] رو میشه از قضیه ی اصلی حلش کرد، که مرتبه ش میشه [tex]n^{\log_4^5}=n^{1+k}[/tex]
خب پس با توجه به رابطه ی بالا می دونیم که : [tex]T(n)\: <\: n^{1+k2}[/tex]
حالا با توجه به این که [tex]T(\frac{n}{6})[/tex] از [tex]T(\frac{n}{4})[/tex] کوچیکتره، اگه توی رابطه تووش بذاریم:
[tex]2T(\frac{n}{6})+3T(\frac{n}{6})=5T(\frac{n}{6})\: <T(n)=2T(\frac{n}{4})+3T(\frac{n}{6})+nlogn\: [/tex] که اگه مرتبه ی سمت چپ رو به دست بیاریم با قضیه ی اصلی که از [tex]T(n)[/tex] مرتبه ش کمتر هست میشه [tex]T(n)=\Omega(nlogn)[/tex]
پس : [tex]nlogn<T(n)<n^{1+k2}[/tex] این فقط حدودش رو داد و حد بالا و پایین یکی نیست که ازش به این نتیجه برسیم که مرتبه ی تابع همون میشه.
من با تغییر متغیر هم رفتم. منتها چون که مجبوریم یه جا جای ۶ عدد دیگه ای بذاریم جواب درست در نیومد.
این فقط حدودش هست و میشه باهاش گزینه حذف کرد. ظاهراََ باید از همون روش بمب اتم رفت. باز دوستانی که بلد هستند انشاالله راهنمایی میکنن.
۰
ارسال: #۵
RE: روابط بازگشتی - روش Akra-Bazi
سلام.سریعترین راه واسه حل اینگونه سوالات همون روش Akra-Bazzi هستش.
ولی این سوال رو با درخت بازگشت هم میشه حل کرد
*فرض میکنیم که شرط اولیه در این سوال T( c ) = d باشه.
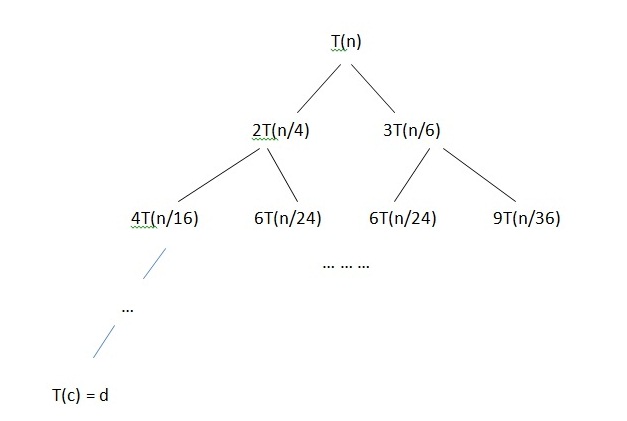
ارتفاع درخت هم برابر [tex]\frac{n}{4^k}\: =\: c\: \: \: \Longrightarrow\: \: k=\log n[/tex] است.
پس در نتیجه:
ولی این سوال رو با درخت بازگشت هم میشه حل کرد
*فرض میکنیم که شرط اولیه در این سوال T( c ) = d باشه.


ارتفاع درخت هم برابر [tex]\frac{n}{4^k}\: =\: c\: \: \: \Longrightarrow\: \: k=\log n[/tex] است.
پس در نتیجه:
[tex]T(n)\: \epsilon\: O(n\: \log n\: \times\: \log n)[/tex]
[tex]T(n)\: \epsilon\: O(n\: \log^2n\: )[/tex]
ارسال: #۶
RE: روابط بازگشتی - روش Akra-Bazi
(۰۹ مهر ۱۳۹۵ ۰۹:۰۹ ب.ظ)Iranian Wizard نوشته شده توسط: سلام.سریعترین راه واسه حل اینگونه سوالات همون روش Akra-Bazzi هستش.
ولی این سوال رو با درخت بازگشت هم میشه حل کرد
*فرض میکنیم که شرط اولیه در این سوال T( c ) = d باشه.
ارتفاع درخت هم برابر [tex]\frac{n}{4^k}\: =\: c\: \: \: \Longrightarrow\: \: k=\log n[/tex] است.
پس در نتیجه:
[tex]T(n)\: \epsilon\: O(n\: \log n\: \times\: \log n)[/tex]
[tex]T(n)\: \epsilon\: O(n\: \log^2n\: )[/tex]
راستش سر این تخمین من قانع نشدم. عبارت جلوی هر لگاریتم به یک عدد نسبتاً قابل توجهی تقسیم شده که رشدش (رشدِ اون عدد) هم نمایی هست اتفاقاً. من کرانِ بالای این عبارات رو گرفتم، یعنی به جای [tex]T(\frac{n}{6})[/tex] اومدم [tex]T(\frac{n}{4})[/tex] گرفتم، یه سری جملاتی مثل [tex]n\cdot\log(n)+\frac{5n}{4}\cdot\log(\frac{n}{4})+\frac{25n}{16}\log(\frac{n}{16})+...[/tex] تولید شد که از یه طرف ضریب پشتِ لگاریتم داره نمایی زیاد میشه، از طرف دیگه کسر داخل لگاریتم هم داره نمایی (و البته نماییتر!) بزرگ میشه. برای همین راحت نمیشه صرف نظر کرد.
ارسال: #۷
RE: روابط بازگشتی - روش Akra-Bazi
(۰۹ مهر ۱۳۹۵ ۱۱:۲۵ ب.ظ)Behnam نوشته شده توسط: راستش سر این تخمین من قانع نشدم. عبارت جلوی هر لگاریتم به یک عدد نسبتاً قابل توجهی تقسیم شده که رشدش (رشدِ اون عدد) هم نمایی هست اتفاقاً. من کرانِ بالای این عبارات رو گرفتم، یعنی به جای [tex]T(\frac{n}{6})[/tex] اومدم [tex]T(\frac{n}{4})[/tex] گرفتم، یه سری جملاتی مثل [tex]n\cdot\log(n)+\frac{5n}{4}\cdot\log(\frac{n}{4})+\frac{25n}{16}\log(\frac{n}{16})+...[/tex] تولید شد که از یه طرف ضریب پشتِ لگاریتم داره نمایی زیاد میشه، از طرف دیگه کسر داخل لگاریتم هم داره نمایی (و البته نماییتر!) بزرگ میشه. برای همین راحت نمیشه صرف نظر کرد.بنظرم میشه صرف نظر کرد.چونکه من اومدم یه جواب بیگ O واسه این سوال پیدا کردم(که به جواب تتای اون نزدیک باشه).و گرنه اگه میخواستم که یک جواب تتا پیدا کنم،حرف شما کاملا درسته.که اونوقت کشیدن و حل درخت بازگشت خیلی سخت میشد.
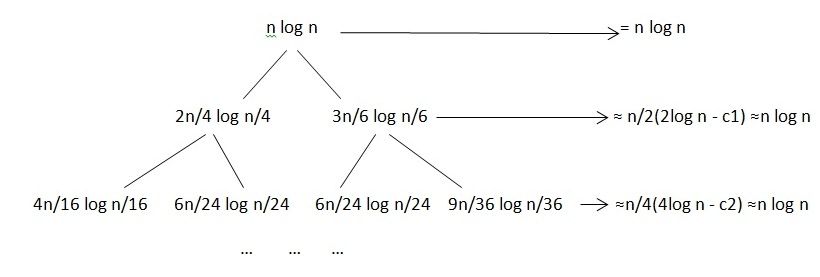
من اینجور حساب کردم:
تو سطر دوم:[tex]\frac{2n}{4}\: \log\: \frac{n}{4}\: +\frac{\: 3n}{6}\: \log\: \frac{n}{6}\: =\frac{\: n}{2}\: \log\: \frac{n}{4}\: +\frac{\: n}{2}\: \log\: \frac{n}{6}\: =\frac{\: n}{2}(\log\: \frac{n}{4}\: +\: \log\: \frac{n}{6})\: =\frac{\: n}{2}\: (\log\: n\: -\: \log\: 4\: +\: \log\: n\: -\: \log\: 6)\: =\frac{\: n}{2}\: (2\log n\: -\: \log4-\log6)\: =\frac{\: n}{2}(2\log n\: -\: c1)\: \approx\: nlogn[/tex]
دلیل اینکه اومدم c1 رو صرف نظر کردم،این بود که من هدفم این بود که یک بیگ O واسه این سوال بدست بیارم.
و تو سطر سوم:
[tex]\frac{4n}{16}\: \log\: \frac{n}{16}\: +\frac{\: 6n}{24}\: \log\: \frac{n}{24}\: +\frac{\: 6n}{24}\: \log\: \frac{n}{24}\: +\frac{\: 9n}{36}\: \log\: \frac{n}{36}\: =\frac{n}{4}\: \log\: \frac{n}{16}\: +\frac{\: n}{4}\: \log\: \frac{n}{24}\: +\frac{\: n}{4}\: \log\: \frac{n}{24}\: +\frac{\: n}{4}\: \log\: \frac{n}{36}=\frac{\: n}{4}(\log\: \frac{n}{16}\: +\: 2\log\: \frac{n}{24}\: +\: \log\: \frac{n}{36})\: =\frac{\: n}{4}\: (4\log\: n\: -\: \log\: 16\: -\: 2\log\: 24\: -\: \log\: 36)\: =\frac{\: n}{4}\: (4\log n\: -\: c2)\: \approx\: nlogn[/tex]
اگه بازم اشتباه میکنم ،حتما بهم بگید.
Can I see some ID?
Feeling left out?
نگران نباش، فقط روی این لینک برای ثبت نام کلیک کن. رمزت رو فراموش کردی؟ اینجا به یادت میاریم! close


