۰
subtitle
ارسال: #۱
ابهام در ماشین های متناهی
سلام دوستان
تو کتاب پارسه و جزوه اقای شاپوری تو این گزاره ها نظر متفاوتی دارن
۱) تعداد حالات اتوماتون های مینیمال [tex]L[/tex] , [tex]\sum^{\ast}-L[/tex] برابر است.
۲) برای هر DFA با چندین وضعیت نهایی DFA ای تنها با یک وضعیت نهایی وجود دارد.
نظر درست کدومه؟
تو کتاب پارسه و جزوه اقای شاپوری تو این گزاره ها نظر متفاوتی دارن
۱) تعداد حالات اتوماتون های مینیمال [tex]L[/tex] , [tex]\sum^{\ast}-L[/tex] برابر است.
۲) برای هر DFA با چندین وضعیت نهایی DFA ای تنها با یک وضعیت نهایی وجود دارد.
نظر درست کدومه؟
۱
ارسال: #۲
RE: ابهام در ماشین های متناهی
(۱۵ دى ۱۳۹۴ ۰۱:۳۰ ق.ظ)sahabi2015 نوشته شده توسط: سلام دوستان
تو کتاب پارسه و جزوه اقای شاپوری تو این گزاره ها نظر متفاوتی دارن
۱) تعداد حالات اتوماتون های مینیمال [tex]L[/tex] , [tex]\sum^{\ast}-L[/tex] برابر است.
۲) برای هر DFA با چندین وضعیت نهایی DFA ای تنها با یک وضعیت نهایی وجود دارد.
نظر درست کدومه؟
سلام
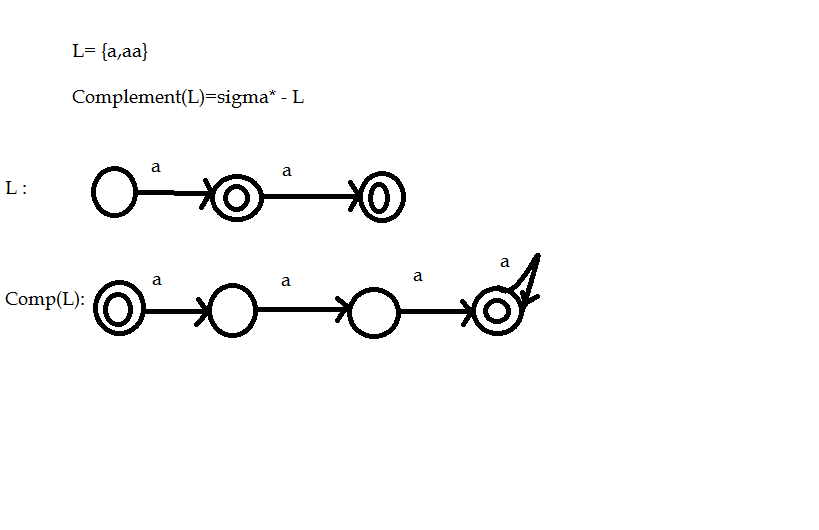
برای سوال دومتون اگه یک زبان منظم و متناهی به صورت {a,aa} داشته باشیم با الفبا ی تک {a} دارد
این ماشین حتما دو حالت فاینال داره که به هیچ عنوانم این ماشین تعداد حالات نهاییش یک تا نمیشه که dfa هم بمونه (اگه nfa میگفت با لامبدا همه رو به یک حالت نهایی میبردیم)
برای سوال اولتون باز به همون زبان دو رشته ای فکر کنید ماشین مینیمالش میشه با سه حالت که دو حالتش فایناله
برای مکمل زبان میشه sigma* -L
که هم q0 حالت فاینال میشه هم q3 فاینال میشه (۴وضعیت و دو فاینال)
دیگه ماشین هاشون برابر با هم نیست
شکل ماشین رسم شده
پس هردو مورد غلطه چون مثال نقض براشون اوردیم دیگه جمله های معتبری نیستند برای هر dfa ایی
ارسال: #۳
RE: ابهام در ماشین های متناهی
(۱۵ دى ۱۳۹۴ ۰۸:۵۲ ب.ظ)mahyamk نوشته شده توسط: سلام
برای سوال دومتون اگه یک زبان منظم و متناهی به صورت {a,aa} داشته باشیم با الفبا ی تک {a} دارد
این ماشین حتما دو حالت فاینال داره که به هیچ عنوانم این ماشین تعداد حالات نهاییش یک تا نمیشه که dfa هم بمونه (اگه nfa میگفت با لامبدا همه رو به یک حالت نهایی میبردیم)
برای سوال اولتون باز به همون زبان دو رشته ای فکر کنید ماشین مینیمالش میشه با سه حالت که دو حالتش فایناله
برای مکمل زبان میشه sigma* -L
که هم q0 حالت فاینال میشه هم q3 فاینال میشه (۴وضعیت و دو فاینال)
دیگه ماشین هاشون برابر با هم نیست
شکل ماشین رسم شده
پس هردو مورد غلطه چون مثال نقض براشون اوردیم دیگه جمله های معتبری نیستند برای هر dfa ایی
سلام. با تشکر از پاسختون به نظرم اگه فرض مساله ۱ روی dfa بودن باشه عبارت درسته. چون فقط جای حالتهای پایانی و غیر پایانی عوض میشه.
۰
ارسال: #۴
RE: ابهام در ماشین های متناهی
ممنونم از پاسختون بانو 
اشتباهات کتاب های کنکوری خیلی زیاده
با نظر اقای جویباری موافقم

اشتباهات کتاب های کنکوری خیلی زیاده
با نظر اقای جویباری موافقم
Can I see some ID?
Feeling left out?
نگران نباش، فقط روی این لینک برای ثبت نام کلیک کن. رمزت رو فراموش کردی؟ اینجا به یادت میاریم! close


