۰
subtitle
ارسال: #۱
درخت بازگشتی این عبارت
سلام دوستان
درخت بازگشتی این عبارت چی میشه؟
[tex]T(n)=T(n-1) T(\frac{n}{2}) n[/tex]
درخت جدا هر کدوم از n-1 و n/2 خیلی راحت میشه کشید اما وقتی باهم هستن جمع میشن چطور باید درختش رو کشید؟
پیشاپیش ممنون دوستان
درخت بازگشتی این عبارت چی میشه؟
[tex]T(n)=T(n-1) T(\frac{n}{2}) n[/tex]
درخت جدا هر کدوم از n-1 و n/2 خیلی راحت میشه کشید اما وقتی باهم هستن جمع میشن چطور باید درختش رو کشید؟
پیشاپیش ممنون دوستان
۱
ارسال: #۳
RE: درخت بازگشتی این عبارت
ارسال: #۴
RE: درخت بازگشتی این عبارت
ارسال: #۵
RE: درخت بازگشتی این عبارت
(۰۴ مهر ۱۳۹۳ ۱۱:۱۴ ب.ظ)miladcr7 نوشته شده توسط:(04 مهر ۱۳۹۳ ۱۱:۰۶ ب.ظ)ziba.O نوشته شده توسط:(04 مهر ۱۳۹۳ ۱۰:۵۹ ب.ظ)miladcr7 نوشته شده توسط: سلام .توی تابع هایی که اینجوری ریتم مختلفی دارند بله
پس چرا تو سوالی که من پرسیدم تو اون یکی تاپیک مرتبه ی دو قسمت بهم ضرب شدند؟
میشه ادرسشو بدید؟؟؟؟
مهمان عزیز شما قادر به مشاهده پیوندهای انجمن مانشت نمیباشید. جهت مشاهده پیوندها ثبت نام کنید.
دوست عزیز معذرت میخوام اینقدر گیج شدم قاطی کردم همه چیو اگه میشه یکم ساده تر اینارو واسم سوا کنین.خدا خیرت بده
ارسال: #۶
RE: درخت بازگشتی این عبارت
(۰۴ مهر ۱۳۹۳ ۱۱:۱۷ ب.ظ)ziba.O نوشته شده توسط:(04 مهر ۱۳۹۳ ۱۱:۱۴ ب.ظ)miladcr7 نوشته شده توسط:(04 مهر ۱۳۹۳ ۱۱:۰۶ ب.ظ)ziba.O نوشته شده توسط:(04 مهر ۱۳۹۳ ۱۰:۵۹ ب.ظ)miladcr7 نوشته شده توسط: سلام .توی تابع هایی که اینجوری ریتم مختلفی دارند بله
پس چرا تو سوالی که من پرسیدم تو اون یکی تاپیک مرتبه ی دو قسمت بهم ضرب شدند؟
میشه ادرسشو بدید؟؟؟؟
مهمان عزیز شما قادر به مشاهده پیوندهای انجمن مانشت نمیباشید. جهت مشاهده پیوندها ثبت نام کنید.
دوست عزیز معذرت میخوام اینقدر گیج شدم قاطی کردم همه چیو اگه میشه یکم ساده تر اینارو واسم سوا کنین.خدا خیرت بده
دقیقا بگو توی چی مشکل داری الان؟؟؟؟؟
ارسال: #۷
RE: درخت بازگشتی این عبارت
(۰۴ مهر ۱۳۹۳ ۱۱:۳۷ ب.ظ)miladcr7 نوشته شده توسط:(04 مهر ۱۳۹۳ ۱۱:۱۷ ب.ظ)ziba.O نوشته شده توسط:(04 مهر ۱۳۹۳ ۱۱:۱۴ ب.ظ)miladcr7 نوشته شده توسط:(04 مهر ۱۳۹۳ ۱۱:۰۶ ب.ظ)ziba.O نوشته شده توسط:(04 مهر ۱۳۹۳ ۱۰:۵۹ ب.ظ)miladcr7 نوشته شده توسط: سلام .توی تابع هایی که اینجوری ریتم مختلفی دارند بله
پس چرا تو سوالی که من پرسیدم تو اون یکی تاپیک مرتبه ی دو قسمت بهم ضرب شدند؟
میشه ادرسشو بدید؟؟؟؟
مهمان عزیز شما قادر به مشاهده پیوندهای انجمن مانشت نمیباشید. جهت مشاهده پیوندها ثبت نام کنید.
دوست عزیز معذرت میخوام اینقدر گیج شدم قاطی کردم همه چیو اگه میشه یکم ساده تر اینارو واسم سوا کنین.خدا خیرت بده
دقیقا بگو توی چی مشکل داری الان؟؟؟؟؟
یه مشکل زیربنایی تو تعیین مرتبه زمانی دارم اون اینه که اگه یه قسمت تابع (T(n-1 باشه بعد با چیز دیگه ای مثل تابع لگاریتمی یا توانی جمع شه مرتبه ی کل تابع چی میشه؟ اسمه روشه حلش چیه؟
ارسال: #۸
RE: درخت بازگشتی این عبارت
iba.O' pid='305268' dateline='1411758772']
یه مشکل زیربنایی تو تعیین مرتبه زمانی دارم اون اینه که اگه یه قسمت تابع (T(n-1 باشه بعد با چیز دیگه ای مثل تابع لگاریتمی یا توانی جمع شه مرتبه ی کل تابع چی میشه؟ اسمه روشه حلش چیه؟
[/quote]
بللللله.


البته الان این خیلی خیلی کلیه.ای کاش یکم جزیی تر میگفتید مثلا توی روش خاصی مشکل دارید یا نه؟؟؟
الان توی روش خاصی مشکل هست یا نه دقیقا توی حل روابط بازگشتی مشکل دارید؟؟؟؟
(۰۴ مهر ۱۳۹۳ ۱۱:۳۷ ب.ظ)miladcr7 نوشته شده توسط:(04 مهر ۱۳۹۳ ۱۱:۱۷ ب.ظ)ziba.O نوشته شده توسط:(04 مهر ۱۳۹۳ ۱۱:۱۴ ب.ظ)miladcr7 نوشته شده توسط:(04 مهر ۱۳۹۳ ۱۱:۰۶ ب.ظ)ziba.O نوشته شده توسط: پس چرا تو سوالی که من پرسیدم تو اون یکی تاپیک مرتبه ی دو قسمت بهم ضرب شدند؟
میشه ادرسشو بدید؟؟؟؟
مهمان عزیز شما قادر به مشاهده پیوندهای انجمن مانشت نمیباشید. جهت مشاهده پیوندها ثبت نام کنید.
دوست عزیز معذرت میخوام اینقدر گیج شدم قاطی کردم همه چیو اگه میشه یکم ساده تر اینارو واسم سوا کنین.خدا خیرت بده
دقیقا بگو توی چی مشکل داری الان؟؟؟؟؟
یه مشکل زیربنایی تو تعیین مرتبه زمانی دارم اون اینه که اگه یه قسمت تابع (T(n-1 باشه بعد با چیز دیگه ای مثل تابع لگاریتمی یا توانی جمع شه مرتبه ی کل تابع چی میشه؟ اسمه روشه حلش چیه؟
[/quote]
بللللله.



البته الان این خیلی خیلی کلیه.ای کاش یکم جزیی تر میگفتید مثلا توی روش خاصی مشکل دارید یا نه؟؟؟
الان توی روش خاصی مشکل هست یا نه دقیقا توی حل روابط بازگشتی مشکل دارید؟؟؟؟
ارسال: #۹
RE: درخت بازگشتی این عبارت
(۰۴ مهر ۱۳۹۳ ۱۱:۵۲ ب.ظ)miladcr7 نوشته شده توسط: iba.O' pid='305268' dateline='1411758772']
(۰۴ مهر ۱۳۹۳ ۱۱:۳۷ ب.ظ)miladcr7 نوشته شده توسط:(04 مهر ۱۳۹۳ ۱۱:۱۷ ب.ظ)ziba.O نوشته شده توسط:(04 مهر ۱۳۹۳ ۱۱:۱۴ ب.ظ)miladcr7 نوشته شده توسط:(04 مهر ۱۳۹۳ ۱۱:۰۶ ب.ظ)ziba.O نوشته شده توسط: پس چرا تو سوالی که من پرسیدم تو اون یکی تاپیک مرتبه ی دو قسمت بهم ضرب شدند؟
میشه ادرسشو بدید؟؟؟؟
مهمان عزیز شما قادر به مشاهده پیوندهای انجمن مانشت نمیباشید. جهت مشاهده پیوندها ثبت نام کنید.
دوست عزیز معذرت میخوام اینقدر گیج شدم قاطی کردم همه چیو اگه میشه یکم ساده تر اینارو واسم سوا کنین.خدا خیرت بده
دقیقا بگو توی چی مشکل داری الان؟؟؟؟؟
یه مشکل زیربنایی تو تعیین مرتبه زمانی دارم اون اینه که اگه یه قسمت تابع (T(n-1 باشه بعد با چیز دیگه ای مثل تابع لگاریتمی یا توانی جمع شه مرتبه ی کل تابع چی میشه؟ اسمه روشه حلش چیه؟
بللللله.



البته الان این خیلی خیلی کلیه.ای کاش یکم جزیی تر میگفتید مثلا توی روش خاصی مشکل دارید یا نه؟؟؟
الان توی روش خاصی مشکل هست یا نه دقیقا توی حل روابط بازگشتی مشکل دارید؟؟؟؟
[/quote]
ببینید اون مسائلی که با مستر حل میشه به کنار، آره تو بقیش مشکل دارم

ارسال: #۱۰
RE: درخت بازگشتی این عبارت
(۰۵ مهر ۱۳۹۳ ۱۲:۰۷ ق.ظ)ziba.O نوشته شده توسط:miladcr7 datelin='1411759348' نوشته شده توسط: iba.O' pid='305268' dateline='1411758772']
(۰۴ مهر ۱۳۹۳ ۱۱:۳۷ ب.ظ)miladcr7 نوشته شده توسط:(04 مهر ۱۳۹۳ ۱۱:۱۷ ب.ظ)ziba.O نوشته شده توسط:(04 مهر ۱۳۹۳ ۱۱:۱۴ ب.ظ)miladcr7 نوشته شده توسط: میشه ادرسشو بدید؟؟؟؟
مهمان عزیز شما قادر به مشاهده پیوندهای انجمن مانشت نمیباشید. جهت مشاهده پیوندها ثبت نام کنید.
دوست عزیز معذرت میخوام اینقدر گیج شدم قاطی کردم همه چیو اگه میشه یکم ساده تر اینارو واسم سوا کنین.خدا خیرت بده
دقیقا بگو توی چی مشکل داری الان؟؟؟؟؟
یه مشکل زیربنایی تو تعیین مرتبه زمانی دارم اون اینه که اگه یه قسمت تابع (T(n-1 باشه بعد با چیز دیگه ای مثل تابع لگاریتمی یا توانی جمع شه مرتبه ی کل تابع چی میشه؟ اسمه روشه حلش چیه؟
بللللله.
البته الان این خیلی خیلی کلیه.ای کاش یکم جزیی تر میگفتید مثلا توی روش خاصی مشکل دارید یا نه؟؟؟
الان توی روش خاصی مشکل هست یا نه دقیقا توی حل روابط بازگشتی مشکل دارید؟؟؟؟
ببینید اون مسائلی که با مستر حل میشه به کنار، آره تو بقیش مشکل دارم

[/quote]
چشم ببینم چیکار میشه کرد.توضیح رو که حتما براتون میدم ولی خب دیگه جامع بودنش رو نمیدونم و اینکه توضیحاتم رو بفهمید هم قولی نمیدم



ارسال: #۱۱
RE: درخت بازگشتی این عبارت
(۰۵ مهر ۱۳۹۳ ۱۲:۱۸ ق.ظ)miladcr7 نوشته شده توسط:(05 مهر ۱۳۹۳ ۱۲:۰۷ ق.ظ)ziba.O نوشته شده توسط:miladcr7 datelin='1411759348' نوشته شده توسط: iba.O' pid='305268' dateline='1411758772']
(۰۴ مهر ۱۳۹۳ ۱۱:۳۷ ب.ظ)miladcr7 نوشته شده توسط:(04 مهر ۱۳۹۳ ۱۱:۱۷ ب.ظ)ziba.O نوشته شده توسط:
مهمان عزیز شما قادر به مشاهده پیوندهای انجمن مانشت نمیباشید. جهت مشاهده پیوندها ثبت نام کنید.
دوست عزیز معذرت میخوام اینقدر گیج شدم قاطی کردم همه چیو اگه میشه یکم ساده تر اینارو واسم سوا کنین.خدا خیرت بده
دقیقا بگو توی چی مشکل داری الان؟؟؟؟؟
یه مشکل زیربنایی تو تعیین مرتبه زمانی دارم اون اینه که اگه یه قسمت تابع (T(n-1 باشه بعد با چیز دیگه ای مثل تابع لگاریتمی یا توانی جمع شه مرتبه ی کل تابع چی میشه؟ اسمه روشه حلش چیه؟
بللللله.
البته الان این خیلی خیلی کلیه.ای کاش یکم جزیی تر میگفتید مثلا توی روش خاصی مشکل دارید یا نه؟؟؟
الان توی روش خاصی مشکل هست یا نه دقیقا توی حل روابط بازگشتی مشکل دارید؟؟؟؟
ببینید اون مسائلی که با مستر حل میشه به کنار، آره تو بقیش مشکل دارم
چشم ببینم چیکار میشه کرد.توضیح رو که حتما براتون میدم ولی خب دیگه جامع بودنش رو نمیدونم و اینکه توضیحاتم رو بفهمید هم قولی نمیدم



[/quote]
شما بفرمایین من سعی میکنم بفهمم
۰
ارسال: #۱۲
RE: درخت بازگشتی این عبارت
بنظرم حد بالای رابطه همون قسمت اول بازگشته که از بازه [tex]O(n^2)[/tex] هستش.
ارسال: #۱۳
RE: درخت بازگشتی این عبارت
۰
۰
ارسال: #۱۵
RE: درخت بازگشتی این عبارت
(۰۴ مهر ۱۳۹۳ ۰۶:۰۷ ب.ظ)ADELZX نوشته شده توسط: بنظرم حد بالای رابطه همون قسمت اول بازگشته که از بازه [tex]O(n^2)[/tex] هستش.
چطور حساب کردید؟
(۰۴ مهر ۱۳۹۳ ۰۷:۲۹ ب.ظ)miladcr7 نوشته شده توسط: سلام.باید n/2. رو حذف کنید و بعد درخت بازگشت رو رسم کنید
چرا باید n/2 حذف بشه؟ فکر کنم تو بازگشت ها تاثیر داشته باش
۰
ارسال: #۱۶
RE: درخت بازگشتی این عبارت
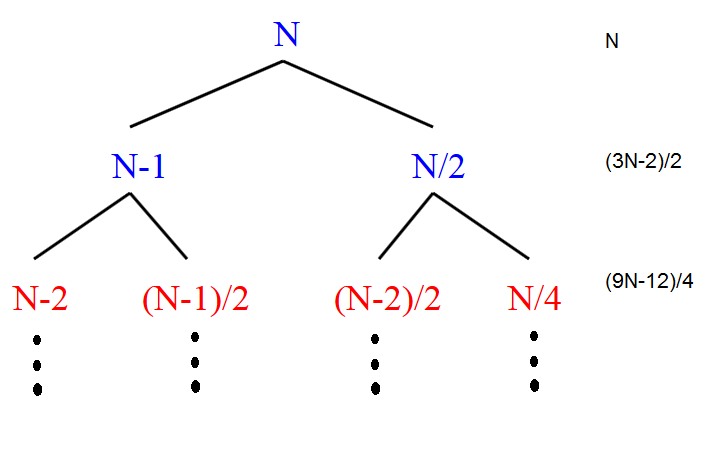
n را ریشه قرار بدید و درخت رسم کنید!هر بار مقدار n در یک سمت درخت یک واحد کم میشه و در سمت دیگه نصف میشه همین طور هر گره جدید رو ادامه میدیم....
حد بالای این تایع در سمتی بدست میاد که n-1 انجام میشه پس مرتبه این تابع از [tex]O(n^2)[/tex] است.
حد بالای این تایع در سمتی بدست میاد که n-1 انجام میشه پس مرتبه این تابع از [tex]O(n^2)[/tex] است.
ارسال: #۱۷
RE: درخت بازگشتی این عبارت
(۰۴ مهر ۱۳۹۳ ۰۹:۰۸ ب.ظ)m@hboobe نوشته شده توسط: n را ریشه قرار بدید و درخت رسم کنید!هر بار مقدار n در یک سمت درخت یک واحد کم میشه و در سمت دیگه نصف میشه همین طور هر گره جدید رو ادامه میدیم....
حد بالای این تایع در سمتی بدست میاد که n-1 انجام میشه پس مرتبه این تابع از [tex]O(n^2)[/tex] است.
قبول اما شما چطور جمع سطوح درخت رو انجام دادید؟ اخه روند خاصی براش به دست نمیاد!
فکر کنم استدلال شما اینطور که ارتفاع که N میشه تو هر سطح هم که یک ضریبی از N داریم پس میشه N^2 درسته؟ اگر اینطوره از کجا میدونید سیگما سطوح رو حساب کنید به N^3 نمیرسه؟
ارسال: #۱۸
RE: درخت بازگشتی این عبارت
(۰۴ مهر ۱۳۹۳ ۰۹:۴۱ ب.ظ)directline نوشته شده توسط:درسته حق با شماست اگر بخواهیم بطور دقیق درخت رسم کنید چنین چیزی به نتیجه جالبی نمیرسیم(04 مهر ۱۳۹۳ ۰۹:۰۸ ب.ظ)m@hboobe نوشته شده توسط: n را ریشه قرار بدید و درخت رسم کنید!هر بار مقدار n در یک سمت درخت یک واحد کم میشه و در سمت دیگه نصف میشه همین طور هر گره جدید رو ادامه میدیم....
حد بالای این تایع در سمتی بدست میاد که n-1 انجام میشه پس مرتبه این تابع از [tex]O(n^2)[/tex] است.
قبول اما شما چطور جمع سطوح درخت رو انجام دادید؟ اخه روند خاصی براش به دست نمیاد!
فکر کنم استدلال شما اینطور که ارتفاع که N میشه تو هر سطح هم که یک ضریبی از N داریم پس میشه N^2 درسته؟ اگر اینطوره از کجا میدونید سیگما سطوح رو حساب کنید به N^3 نمیرسه؟
ولی حداقل با همین روش که کاملا هم درست نیست (اگر دقت کنید جلوی جمله رسم درختم علامت تعجب گذاشتم
 ) متوجه میشیم که اگر بخواهیم محاسبه رو با اون قسمت از تایع که هر بار یک واحد کم میکنه انجام بدیم ارتفاع بیشتری داریم (با توجه به صحبتهای سایر بچه ها = دیر تر به یک نزدیک میشه!) پس اون بخش موثر در حل هست
) متوجه میشیم که اگر بخواهیم محاسبه رو با اون قسمت از تایع که هر بار یک واحد کم میکنه انجام بدیم ارتفاع بیشتری داریم (با توجه به صحبتهای سایر بچه ها = دیر تر به یک نزدیک میشه!) پس اون بخش موثر در حل هستمن خودم اولین بار که به این مساله برخورد کردم اینجور درنظر گرفتم که ممکنه هر بار یه بخش از این تابع اتفاق بیفته با n-1 مرتبه که [tex]Theta(n^2)[/tex] شد و با n/2 از طریق مستر شد [tex]Theta(n)[/tex] که گفتم کران بالای حل میشه [tex]O(n^2)[/tex]

امیدوارم که با توضیحاتم گیج نشده باشید
موفق باشین
۰
ارسال: #۱۹
RE: درخت بازگشتی این عبارت
سلام این مثال چون از دو تابع کاملا متفاوت تشکیل شده حل دقیقی نداره ولی روش حل تقریبیش اینه که اون تابعی که زودتر به یک میرسه رو بیخیال میشیم خب؟
حالا توی این مثال n/2 داره سریعتر به یک نزدیک میشه پس میتونیم حذفش کنیم یا یه روش دیگه برای حذف اینه که اون تابعی که زمان اجرای کمتری داره رو حذف میکنیم چون بازم زودتر به یک میرسه حالا دقت کن که مرتبه اجرای n/2 لگاریتمی هستش و اون یکی تابع مرتبش از n هست پس n/2 رو حذف کن حالا تابع باقیمونده مرتبه اجراش n به توان دو میشه
اکی؟؟؟


حالا توی این مثال n/2 داره سریعتر به یک نزدیک میشه پس میتونیم حذفش کنیم یا یه روش دیگه برای حذف اینه که اون تابعی که زمان اجرای کمتری داره رو حذف میکنیم چون بازم زودتر به یک میرسه حالا دقت کن که مرتبه اجرای n/2 لگاریتمی هستش و اون یکی تابع مرتبش از n هست پس n/2 رو حذف کن حالا تابع باقیمونده مرتبه اجراش n به توان دو میشه
اکی؟؟؟



۰
ارسال: #۲۰
RE: درخت بازگشتی این عبارت
یعنی میشه اینطوری نتیجه گیری کلی کرد؟؟؟؟؟ ( اگه تابعی از مجموع چندین مرتبه مختلف تشکیل شده باشه ، بیشترین مرتبه مرتبه اجرایی اون تابعه؟)

۰
۰
ارسال: #۲۲
RE: درخت بازگشتی این عبارت
(۰۴ مهر ۱۳۹۳ ۰۵:۱۵ ب.ظ)directline نوشته شده توسط: سلام دوستان
درخت بازگشتی این عبارت چی میشه؟
[tex]T(n)=T(n-1) T(\frac{n}{2}) n[/tex]
درخت جدا هر کدوم از n-1 و n/2 خیلی راحت میشه کشید اما وقتی باهم هستن جمع میشن چطور باید درختش رو کشید؟
پیشاپیش ممنون دوستان
اینو بخون
مهمان عزیز شما قادر به مشاهده پیوندهای انجمن مانشت نمیباشید. جهت مشاهده پیوندها ثبت نام کنید.
۰
ارسال: #۲۳
RE: درخت بازگشتی این عبارت
(۰۴ مهر ۱۳۹۳ ۰۵:۱۵ ب.ظ)directline نوشته شده توسط: سلام دوستان
درخت بازگشتی این عبارت چی میشه؟
[tex]T(n)=T(n-1) T(\frac{n}{2}) n[/tex]
درخت جدا هر کدوم از n-1 و n/2 خیلی راحت میشه کشید اما وقتی باهم هستن جمع میشن چطور باید درختش رو کشید؟
پیشاپیش ممنون دوستان
قبلا هم گفتیم این معادله حل دقیق نداره ولی n/2 رو حذف میکنیم و تقریبی حلش میکنیم
موضوعهای مرتبط با این موضوع... |
|||||
| موضوع: | نویسنده | پاسخ: | بازدید: | آخرین ارسال | |
| تعداد برگ درخت؟؟؟؟؟؟؟ | rad.bahar | ۴ | ۶,۷۳۱ |
۱۵ آذر ۱۴۰۲ ۱۱:۵۳ ق.ظ آخرین ارسال: mohamadrra |
|
| کمک در باره این تروجان | Ghasemiyeh | ۲ | ۴,۱۱۶ |
۲۵ آذر ۱۴۰۰ ۰۳:۰۰ ق.ظ آخرین ارسال: one hacker alone |
|
| دو سوال در مورد درخت BST(درخت جستجوی دودویی) | امیدوار | ۳ | ۷,۰۰۰ |
۱۰ دى ۱۳۹۹ ۱۲:۰۴ ق.ظ آخرین ارسال: marzi.pnh |
|
| زمان جستجوی درخت | fateme.sm | ۰ | ۲,۴۵۳ |
۰۶ دى ۱۳۹۹ ۱۰:۴۱ ب.ظ آخرین ارسال: fateme.sm |
|
| مرتبه ایجاد درخت | rad.bahar | ۱ | ۴,۳۳۴ |
۳۰ مهر ۱۳۹۹ ۰۳:۳۴ ب.ظ آخرین ارسال: rad.bahar |
|
| چگونه این خطا را موقع اجرای sql server 2014 رفع کنم ؟ | farahnaz | ۲ | ۴,۴۲۸ |
۱۹ مهر ۱۳۹۹ ۰۲:۱۸ ق.ظ آخرین ارسال: farahnaz |
|
| عمق درخت ???? | rad.bahar | ۱ | ۳,۳۸۱ |
۱۱ مهر ۱۳۹۹ ۰۳:۳۱ ب.ظ آخرین ارسال: عزیز دادخواه |
|
| محاسبه ارتفاع درخت.... | baharkhanoom | ۳ | ۹,۷۲۴ |
۰۹ اردیبهشت ۱۳۹۹ ۰۶:۴۸ ب.ظ آخرین ارسال: mohsentafresh |
|
| پایتون (طراحی وب یا دیتا ساینس؟) مساله این است... | sirvan.t | ۲ | ۴,۹۰۴ |
۱۹ بهمن ۱۳۹۸ ۱۲:۰۱ ب.ظ آخرین ارسال: sirvan.t |
|
| تعداد درخت فراگیر | ss311 | ۰ | ۲,۹۸۶ |
۰۶ بهمن ۱۳۹۸ ۰۵:۰۶ ب.ظ آخرین ارسال: ss311 |
|
Can I see some ID?
Feeling left out?
نگران نباش، فقط روی این لینک برای ثبت نام کلیک کن. رمزت رو فراموش کردی؟ اینجا به یادت میاریم! close



