۰
subtitle
ارسال: #۱
 سوال از دسترسی تصادفی به روش Slotted Aloha
سوال از دسترسی تصادفی به روش Slotted Aloha
فرض کنید یک شبکه توکن رینگ با توپولوژی فیزیکی ستاره با ۱۰۰۰ ایستگاه داریم که فاصله هر ایستگاه تا MAU برابر ۱۰۰ متر، نرخ ارسال ۴ مگابیت در ثانیه، اندازه فریم های داده ۱۰۰۰ بایت باشد. اگر فرض کنیم سرعت انتشار امواج ۸^۱۰*۲ متر برثانیه و تاخیر در هر ایستگاه ۴ بیت باشد. کارایی این شبکه تقریبا برابر است با:
(شبکه های کاپیوتریIT - سراسری ۸۷) (تست شماره ۳۹ پارسه)
چرا در حل این مسئله از فرمول اصلی یعنی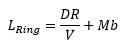 استفاده نکرده است و مسئله را به طریق دیگر حل نموده است؟
استفاده نکرده است و مسئله را به طریق دیگر حل نموده است؟
(شبکه های کاپیوتریIT - سراسری ۸۷) (تست شماره ۳۹ پارسه)
چرا در حل این مسئله از فرمول اصلی یعنی
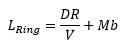 استفاده نکرده است و مسئله را به طریق دیگر حل نموده است؟
استفاده نکرده است و مسئله را به طریق دیگر حل نموده است؟
۰
ارسال: #۲
RE: سوال از دسترسی تصادفی به روش Slotted Aloha
من اینطوری تحلیل کردم:
اول اینکه یه سیستم مرکزی داریم (چون توپولوژی استار داریم) که هر ایستگاهی به فاصله ی ۱۰۰ متر از اون قرار گرفته.پس فاصله هر ایستگاه تا مرکز ۱۰۰ هست.چون استار هست بنابراین هر بسته اول می ره به مرکز و بعد به ایستگاه بعدی ارسال میشه.بنابراین برای اینکه یه بسته از یه سیستم به سیستم کناری منتقل شه ---> 200=2*100 .
۱۰۰۰ تا ایستگاه داریم بنابراین تعدادشون و هم ضرب می کنیم.بنابراین یه بسته برای اینکه یه دور کامل بره باید ۵^۱۰*۲ متر رو باید طی کنه.
برای اینکه کارایی به دست بیاد باید حداقل زمان ارسال یه بسته رو در حالت ایده آل تقسیم به مدت زمانی کنیم که با شرایط مسئله طول می کشه تا بسته برسه.مسلما در حالت ایده آل تنها تاخیر تاخیر انتقال هست که برابر با [tex]L/R[/tex] هست.
تاخیر تو مسئله هم برابر با مجموع تمام تاخیر هاست که اینجا برابر با تاخیر انتشار + تاخیر انتقال + تاخیر تمام ایستگاه ها هست.
حالا از تقسیم تاخیر ایده آل به تاخیر مسئله جواب به دست می آد.
[tex]\frac{L}{R}= \frac{1000*8}{4*10^6}=2*10^{-3}[/tex]
تاخیر مسئله هم اگر حساب کنیم برابر میشه با [tex]4*10^{-3}[/tex]
که از تقسیم این ذو تا و ضرب در جواب ذر ۱۰۰ جواب به دست می اد که می شه ۵۰ درصد.
اول اینکه یه سیستم مرکزی داریم (چون توپولوژی استار داریم) که هر ایستگاهی به فاصله ی ۱۰۰ متر از اون قرار گرفته.پس فاصله هر ایستگاه تا مرکز ۱۰۰ هست.چون استار هست بنابراین هر بسته اول می ره به مرکز و بعد به ایستگاه بعدی ارسال میشه.بنابراین برای اینکه یه بسته از یه سیستم به سیستم کناری منتقل شه ---> 200=2*100 .
۱۰۰۰ تا ایستگاه داریم بنابراین تعدادشون و هم ضرب می کنیم.بنابراین یه بسته برای اینکه یه دور کامل بره باید ۵^۱۰*۲ متر رو باید طی کنه.
برای اینکه کارایی به دست بیاد باید حداقل زمان ارسال یه بسته رو در حالت ایده آل تقسیم به مدت زمانی کنیم که با شرایط مسئله طول می کشه تا بسته برسه.مسلما در حالت ایده آل تنها تاخیر تاخیر انتقال هست که برابر با [tex]L/R[/tex] هست.
تاخیر تو مسئله هم برابر با مجموع تمام تاخیر هاست که اینجا برابر با تاخیر انتشار + تاخیر انتقال + تاخیر تمام ایستگاه ها هست.
حالا از تقسیم تاخیر ایده آل به تاخیر مسئله جواب به دست می آد.
[tex]\frac{L}{R}= \frac{1000*8}{4*10^6}=2*10^{-3}[/tex]
تاخیر مسئله هم اگر حساب کنیم برابر میشه با [tex]4*10^{-3}[/tex]
که از تقسیم این ذو تا و ضرب در جواب ذر ۱۰۰ جواب به دست می اد که می شه ۵۰ درصد.
۰
ارسال: #۳
RE: سوال از دسترسی تصادفی به روش Slotted Aloha
فرمولی که نشون دادی برای حالت همبندی حلقه است ولی در این سئوال همبندی ستاره ای است که داده اول به MAU داده میشه بعد
MAU اون رو بلافاصله به مقصد میرسونه پس فاصله تا مقصد برابر با (فاصله مبداء تا MAU + MAU تا مقصد)
MAU اون رو بلافاصله به مقصد میرسونه پس فاصله تا مقصد برابر با (فاصله مبداء تا MAU + MAU تا مقصد)
۰
ارسال: #۴
سوال از دسترسی تصادفی به روش Slotted Aloha
فکر کنم به جای حفظ کردن فرمول ها اگر با تحلیل این مسئله هارو حل کنید بهتر باشه.
۰
ارسال: #۵
سوال از دسترسی تصادفی به روش Slotted Aloha
Can I see some ID?
Feeling left out?
نگران نباش، فقط روی این لینک برای ثبت نام کلیک کن. رمزت رو فراموش کردی؟ اینجا به یادت میاریم! close
