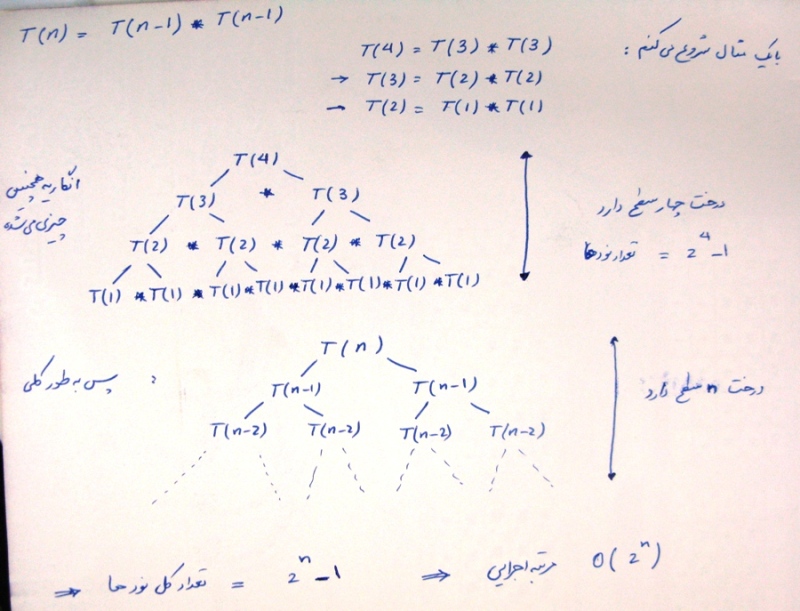
اگر تابع [tex]t(n)=t(n-1)*t(n-1)[/tex] تو گسسته مطرح میشد و از شما خواسته میشد که جواب غیر بازگشتی تابع رو به دست بیارید اونوقت باید از روش های معمول حل روابط بازگشتی استفاده می کردید و جواب رو به دست می آوردید.اما چون تو بحث ساختمان و مرتبه اجرایی به دنبال تعداد کل فراخوانی های تابع t هستیم پس می تونیم علامت ضرب موجود در صورت سوال رو به جمع تبدیل کنیم.یعنی تابع [tex]t(n)=t(n-1)*t(n-1)[/tex] رو به صورت [tex]t(n)=t(n-1) t(n-1)=2t(n-1)[/tex] در نظر بگیریم .حالا میتونیم با روش جایگذاری، تعداد فراخوانی های t رو به دست بیاریم:
[tex]t(n)=2t(n-1)[/tex]
[tex]t(n)=2(2t(n-2))[/tex]
.
.
.
[tex]t(n)=2^{n-1}(t(1))[/tex]
همونطور که مشخصه تابع بازگشتی از مرتبه دو به توان n هستش