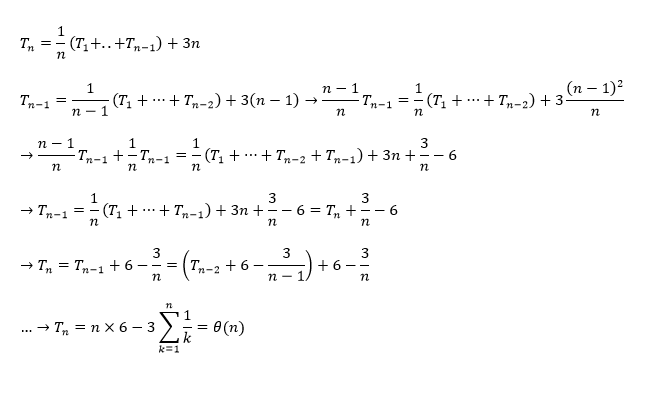۰
subtitle
ارسال: #۱
مرتبه زمانی از کتاب نارنجی استاد یوسفی
سلام اینو اگه میشه واسه من توضیح بدین چی میشه ممنون [tex]T\: (n)\: =\: \frac{1}{n}\sum_{i=1}^{n-1}T(i)\: +\: 3n\: \: \: \: \: \: \: \: \: \: T(1)\: =\: 1[/tex]
۲
ارسال: #۲
RE: مرتبه زمانی از کتاب نارنجی استاد یوسفی
سلام. معمولا توی اکثر موارد که مرتبه ی زمانی یک سری رو میخواد و [tex]T(n)[/tex] مساوی با یک سری هست، میایم [tex]T(n-1)[/tex] رو مینویسیم. به این دلیل که جملات اینا با هم دیگه بره و ساده بشه عبارت.
[tex]T(n)=\frac{1}{n}\sum^{n-1}_{i=1}T(i)+3n=\frac{1}{n}\times(T(1)+T(2)+T(3)+...+T(n-1)+3n[/tex]
و حالا رو مینویسیم:
[tex]T(n-۱)=\frac{1}{n-۱}\sum^{n-2}_{i=1}T(i)+3(n-1)=\frac{1}{n-1}\times(T(1)+T(2)+T(3)+...+T(n-2)+3(n-1)[/tex]
یه طوری میخوایم اینا رو ساده کنیم با هم. (اینم یه قانونه معمولا که باید از شر ضریب سری خلاص بشید. معمولا این طوری هست.)
این جا واسه ساده کردن این دو سری با هم، سری اول رو در n و سری دوم رو در n-1 ضرب میکنیم تا اون ضریب کسری از بین بره.
[tex](n)T(n)=\sum^{n-1}_{i=1}T(i)+3(n)^2=(T(1)+T(2)+T(3)+...+T(n-1))+3(n)^2[/tex]
[tex](n-1)T(n-۱)=\sum^{n-2}_{i=1}T(i)+3(n-1)^2=(T(1)+T(2)+T(3)+...+T(n-2))+3(n-1)^2[/tex]
الان میبینیم که جملات سری ها میتونن با هم برن. عبارت اول رو منهای عبارت دوم میکنیم تا از شر جملات سری خلاص بشیم تا جایی که ممکن هست:
[tex]nT(n)-(n-1)T(n-1)=\sum^{n-1}_{i=1}T(i)+3(n)^2-\sum_{i=1}^{n-2}T(i)=(T(1)+T(2)+T(3)+...+T(n-1))+3(n)^2-[T(1)+T(2)+....+T(n-2)+3(n-1)^2][/tex]
حالا :
[tex]nT(n)-(n-1)T(n-1)=T(n-1)+3n^2-3(n-1)^2=T(n-1)+3n^2-3n^2-3+6n[/tex]
[tex]nT(n)-(n-1)T(n)=T(n-1)+6n-3[/tex]
[tex]nT(n)=nT(n-1)+6n-3[/tex]
طرفین رو بر n تقسیم میکنیم. میشه:
[tex]T(n)=T(n-1)+\frac{(6n-3)}{n}\: \: =>\: T(n)=T(n-1)+\theta(1)[/tex] که از مرتبه ی [tex]\theta(n)[/tex] هست.
[tex]T(n)=\frac{1}{n}\sum^{n-1}_{i=1}T(i)+3n=\frac{1}{n}\times(T(1)+T(2)+T(3)+...+T(n-1)+3n[/tex]
و حالا رو مینویسیم:
[tex]T(n-۱)=\frac{1}{n-۱}\sum^{n-2}_{i=1}T(i)+3(n-1)=\frac{1}{n-1}\times(T(1)+T(2)+T(3)+...+T(n-2)+3(n-1)[/tex]
یه طوری میخوایم اینا رو ساده کنیم با هم. (اینم یه قانونه معمولا که باید از شر ضریب سری خلاص بشید. معمولا این طوری هست.)
این جا واسه ساده کردن این دو سری با هم، سری اول رو در n و سری دوم رو در n-1 ضرب میکنیم تا اون ضریب کسری از بین بره.
[tex](n)T(n)=\sum^{n-1}_{i=1}T(i)+3(n)^2=(T(1)+T(2)+T(3)+...+T(n-1))+3(n)^2[/tex]
[tex](n-1)T(n-۱)=\sum^{n-2}_{i=1}T(i)+3(n-1)^2=(T(1)+T(2)+T(3)+...+T(n-2))+3(n-1)^2[/tex]
الان میبینیم که جملات سری ها میتونن با هم برن. عبارت اول رو منهای عبارت دوم میکنیم تا از شر جملات سری خلاص بشیم تا جایی که ممکن هست:
[tex]nT(n)-(n-1)T(n-1)=\sum^{n-1}_{i=1}T(i)+3(n)^2-\sum_{i=1}^{n-2}T(i)=(T(1)+T(2)+T(3)+...+T(n-1))+3(n)^2-[T(1)+T(2)+....+T(n-2)+3(n-1)^2][/tex]
حالا :
[tex]nT(n)-(n-1)T(n-1)=T(n-1)+3n^2-3(n-1)^2=T(n-1)+3n^2-3n^2-3+6n[/tex]
[tex]nT(n)-(n-1)T(n)=T(n-1)+6n-3[/tex]
[tex]nT(n)=nT(n-1)+6n-3[/tex]
طرفین رو بر n تقسیم میکنیم. میشه:
[tex]T(n)=T(n-1)+\frac{(6n-3)}{n}\: \: =>\: T(n)=T(n-1)+\theta(1)[/tex] که از مرتبه ی [tex]\theta(n)[/tex] هست.
ارسال: #۳
RE: مرتبه زمانی از کتاب نارنجی استاد یوسفی
(۲۷ مهر ۱۳۹۵ ۰۸:۵۵ ب.ظ)Pure Liveliness نوشته شده توسط: سلام. معمولا توی اکثر موارد که مرتبه ی زمانی یک سری رو میخواد و [tex]T(n)[/tex] مساوی با یک سری هست، میایم [tex]T(n-1)[/tex] رو مینویسیم. به این دلیل که جملات اینا با هم دیگه بره و ساده بشه عبارت.
[tex]T(n)=\frac{1}{n}\sum^{n-1}_{i=1}T(i)+3n=\frac{1}{n}\times(T(1)+T(2)+T(3)+...+T(n-1)+3n[/tex]
و حالا رو مینویسیم:
[tex]T(n-۱)=\frac{1}{n-۱}\sum^{n-2}_{i=1}T(i)+3(n-1)=\frac{1}{n-1}\times(T(1)+T(2)+T(3)+...+T(n-2)+3(n-1)[/tex]
یه طوری میخوایم اینا رو ساده کنیم با هم. (اینم یه قانونه معمولا که باید از شر ضریب سری خلاص بشید. معمولا این طوری هست.)
این جا واسه ساده کردن این دو سری با هم، سری اول رو در n و سری دوم رو در n-1 ضرب میکنیم تا اون ضریب کسری از بین بره.
[tex](n)T(n)=\sum^{n-1}_{i=1}T(i)+3(n)^2=(T(1)+T(2)+T(3)+...+T(n-1))+3(n)^2[/tex]
[tex](n-1)T(n-۱)=\sum^{n-2}_{i=1}T(i)+3(n-1)^2=(T(1)+T(2)+T(3)+...+T(n-2))+3(n-1)^2[/tex]
الان میبینیم که جملات سری ها میتونن با هم برن. عبارت اول رو منهای عبارت دوم میکنیم تا از شر جملات سری خلاص بشیم تا جایی که ممکن هست:
[tex]nT(n)-(n-1)T(n-1)=\sum^{n-1}_{i=1}T(i)+3(n)^2-\sum_{i=1}^{n-2}T(i)=(T(1)+T(2)+T(3)+...+T(n-1))+3(n)^2-[T(1)+T(2)+....+T(n-2)+3(n-1)^2][/tex]
حالا :
[tex]nT(n)-(n-1)T(n-1)=T(n-1)+3n^2-3(n-1)^2=T(n-1)+3n^2-3n^2-3+6n[/tex]
[tex]nT(n)-(n-1)T(n)=T(n-1)+6n-3[/tex]
[tex]nT(n)=nT(n-1)+6n-3[/tex]
طرفین رو بر n تقسیم میکنیم. میشه:
[tex]T(n)=T(n-1)+\frac{(6n-3)}{n}\: \: =>\: T(n)=T(n-1)+\theta(1)[/tex] که از مرتبه ی [tex]\theta(n)[/tex] هست.
nT(n)=nT(n-1)+6n-3 اینو نفهمیدم چرا اینطوری شد





ارسال: #۴
RE: مرتبه زمانی از کتاب نارنجی استاد یوسفی
ارسال: #۵
RE: مرتبه زمانی از کتاب نارنجی استاد یوسفی
(۲۷ مهر ۱۳۹۵ ۱۰:۲۱ ب.ظ)Pure Liveliness نوشته شده توسط:(27 مهر ۱۳۹۵ ۰۹:۵۹ ب.ظ)omidxp نوشته شده توسط: nT(n)=nT(n-1)+6n-3 اینو نفهمیدم چرا اینطوری شدچون:
[tex]nT(n)-(n-1)T(n-1)=T(n-1)+6n-3\: =>\: nT(n)=(n-1)T(n-1)+T(n-1)+6n-1=nT(n-1)-T(n-1)+T(n-1)+6n-3=nT(n-1)+6n-3[/tex]
خیلی ممنون ازتون عالی بود پاسختون
ارسال: #۶
RE: مرتبه زمانی از کتاب نارنجی استاد یوسفی
(۲۸ مهر ۱۳۹۵ ۰۳:۳۹ ب.ظ)omidxp نوشته شده توسط:خواهش میکنم.(27 مهر ۱۳۹۵ ۱۰:۲۱ ب.ظ)Pure Liveliness نوشته شده توسط:خیلی ممنون ازتون عالی بود پاسختون(27 مهر ۱۳۹۵ ۰۹:۵۹ ب.ظ)omidxp نوشته شده توسط: nT(n)=nT(n-1)+6n-3 اینو نفهمیدم چرا اینطوری شدچون:
[tex]nT(n)-(n-1)T(n-1)=T(n-1)+6n-3\: =>\: nT(n)=(n-1)T(n-1)+T(n-1)+6n-1=nT(n-1)-T(n-1)+T(n-1)+6n-3=nT(n-1)+6n-3[/tex]
۱
ارسال: #۷
RE: مرتبه زمانی از کتاب نارنجی استاد یوسفی
Can I see some ID?
Feeling left out?
نگران نباش، فقط روی این لینک برای ثبت نام کلیک کن. رمزت رو فراموش کردی؟ اینجا به یادت میاریم! close