۲
subtitle
ارسال: #۱
نحوه محاسبه مرتبه زمانی
سلام دوستان.
خسته نباشید.
میشه نحوه محاسبه مرتبه زمانی این شبه کد رو مرحله به مرحله توضیح بدین؟
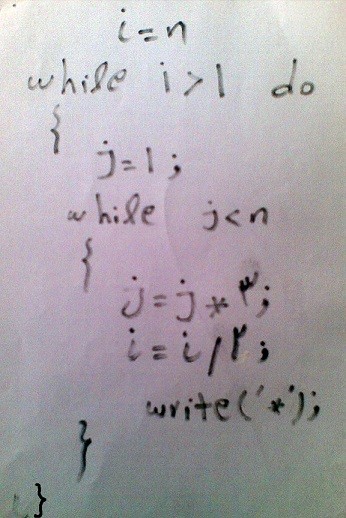
سپاسگذارم.
خسته نباشید.
میشه نحوه محاسبه مرتبه زمانی این شبه کد رو مرحله به مرحله توضیح بدین؟
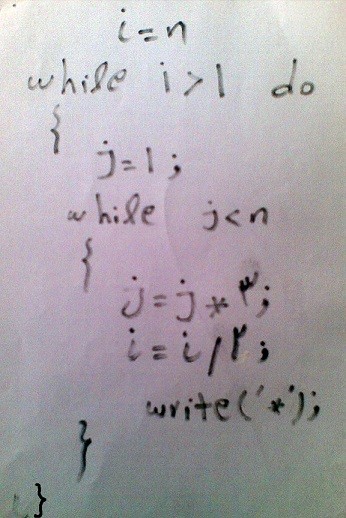
سپاسگذارم.
۳
۳
ارسال: #۳
RE: نحوه محاسبه مرتبه زمانی
قبلا به جای تقسیم گذاشته بودید * و من نوشتم دیدم حلقه ی بی نهایت میشه و جواب نداره.
الان که تبدیل به تقسیم کردید دوباره حل کردم.
اول : i=n
تا زمانی که i از ۱ بزرگتر هست، دستورات داخل while اول اجرا میشه.
……………….j=1
……………...تا زمانی که j از n کوچک تر هست، دستورات داخلی while دوم اجرا میشه.
……………………………. j=j*3
………………..……………i=i/2
………………..……………*write
j=1 هر بار در ۳ ضرب میشه تا برسه به n که از شرط while دوم بیرون بیایم. [tex]\log_3n[/tex] بار j در سه ضرب میشه تا برسه به n. دستور چاپ * هم به تعداد [tex]\log_3n[/tex] بار اجرا میشه.
وقتی j به n رسید i چند شده؟ i که قبل از این while دوم n بود الان هر بار با ضربدر ۳ شدن j, تقسیم بر ۲ شده. یعنی[tex]\log_3n[/tex] بار بر ۲ تقسیم شده.
یعنی برای while داخلی:
j=3 ….. i=n/2
[tex]j=3^{2\: }........i=\frac{n}{2^2}[/tex]
[tex]j=3^{3\: }........i=\frac{n}{2^3}[/tex]
[tex]j=3^{4\: }........i=\frac{n}{2^4}[/tex]
.
.
.[tex]j=3^k\: ........i=\frac{n}{2^k}[/tex]
تا جایی این ضرب در ۳ برای j ادامه داره که به n برسه. یعنی :
[tex]3^k<=n[/tex]
[tex]k=\log_3n[/tex]
پس در انتهای حلقه ی while، مقدار i هم شده [tex]\frac{n}{2^k}=\frac{n}{(2^{\log_3n})}=\frac{n}{n^{\log_32}}=\frac{n}{n^{1-t}}[/tex]
در این جا [tex]\log_3n[/tex] بار عمل چاپ * انجام شده.
حالا از while دوم مییایم بیرون. شرط while اول برقرار هست، چون i از ۱ بزرگتر هست و دوباره j=1 میشه و به همون ترتیب بالا.
نکته ای که وجود داره این هست که چند بار حلقه ی while دوم انجام میشه؟ و در واقع i تا کی از ۱ بزرگتر خواهد موند؟
واضح هست که زمانی شرط حلقه ی اول نقض میشه که i=1 بشه یا مقداری کمتر از ۱.
الان بعد از یک بار اجرای حلقه ی دوم که مقدار i بزرگتر از یک هست دوباره شرط while اول درست هست و میایم داخل حلقه.
j=1
[tex]j=3\: ......\: i=\frac{n}{n^{\log_32}\cdot2}[/tex] که i مقدارش از ۱ کمتر میشه. اما این شرط حلقه رو که [tex]j<n[/tex] رو نقض نمیکنه. پس این while دوم هم [tex]\log_3n[/tex] بار اجرا میشه تا از while دوم بیاد بیرون. در این جا مقدار i برابر شده با [tex]\frac{n}{n^{2\log_32}}[/tex]
حالا شرط while اول چک میشه. غلط هست چون i از ۱ کوچیکتر هست. پس کلا دو تا [tex]\log_3n[/tex] بار دستورات انجام شد و در نتیجه مرتبه ی زمانی برابر میشه با [tex]\theta(\log_3n)[/tex]
الان که تبدیل به تقسیم کردید دوباره حل کردم.
اول : i=n
تا زمانی که i از ۱ بزرگتر هست، دستورات داخل while اول اجرا میشه.
……………….j=1
……………...تا زمانی که j از n کوچک تر هست، دستورات داخلی while دوم اجرا میشه.
……………………………. j=j*3
………………..……………i=i/2
………………..……………*write
j=1 هر بار در ۳ ضرب میشه تا برسه به n که از شرط while دوم بیرون بیایم. [tex]\log_3n[/tex] بار j در سه ضرب میشه تا برسه به n. دستور چاپ * هم به تعداد [tex]\log_3n[/tex] بار اجرا میشه.
وقتی j به n رسید i چند شده؟ i که قبل از این while دوم n بود الان هر بار با ضربدر ۳ شدن j, تقسیم بر ۲ شده. یعنی[tex]\log_3n[/tex] بار بر ۲ تقسیم شده.
یعنی برای while داخلی:
j=3 ….. i=n/2
[tex]j=3^{2\: }........i=\frac{n}{2^2}[/tex]
[tex]j=3^{3\: }........i=\frac{n}{2^3}[/tex]
[tex]j=3^{4\: }........i=\frac{n}{2^4}[/tex]
.
.
.[tex]j=3^k\: ........i=\frac{n}{2^k}[/tex]
تا جایی این ضرب در ۳ برای j ادامه داره که به n برسه. یعنی :
[tex]3^k<=n[/tex]
[tex]k=\log_3n[/tex]
پس در انتهای حلقه ی while، مقدار i هم شده [tex]\frac{n}{2^k}=\frac{n}{(2^{\log_3n})}=\frac{n}{n^{\log_32}}=\frac{n}{n^{1-t}}[/tex]
در این جا [tex]\log_3n[/tex] بار عمل چاپ * انجام شده.
حالا از while دوم مییایم بیرون. شرط while اول برقرار هست، چون i از ۱ بزرگتر هست و دوباره j=1 میشه و به همون ترتیب بالا.
نکته ای که وجود داره این هست که چند بار حلقه ی while دوم انجام میشه؟ و در واقع i تا کی از ۱ بزرگتر خواهد موند؟
واضح هست که زمانی شرط حلقه ی اول نقض میشه که i=1 بشه یا مقداری کمتر از ۱.
الان بعد از یک بار اجرای حلقه ی دوم که مقدار i بزرگتر از یک هست دوباره شرط while اول درست هست و میایم داخل حلقه.
j=1
[tex]j=3\: ......\: i=\frac{n}{n^{\log_32}\cdot2}[/tex] که i مقدارش از ۱ کمتر میشه. اما این شرط حلقه رو که [tex]j<n[/tex] رو نقض نمیکنه. پس این while دوم هم [tex]\log_3n[/tex] بار اجرا میشه تا از while دوم بیاد بیرون. در این جا مقدار i برابر شده با [tex]\frac{n}{n^{2\log_32}}[/tex]
حالا شرط while اول چک میشه. غلط هست چون i از ۱ کوچیکتر هست. پس کلا دو تا [tex]\log_3n[/tex] بار دستورات انجام شد و در نتیجه مرتبه ی زمانی برابر میشه با [tex]\theta(\log_3n)[/tex]
Can I see some ID?
Feeling left out?
نگران نباش، فقط روی این لینک برای ثبت نام کلیک کن. رمزت رو فراموش کردی؟ اینجا به یادت میاریم! close


