۰
subtitle
ارسال: #۱
بدست آوردن O,o,w,Ω,θ در مسائل
با سلام
من در به دست آوردن مرتبه اجرایی مشکل دارم.مثلا تعاریف O,o,w,Ω,θ رو خوندم ولی نمی دونم چطور در مسائل ازشون استفاده کنم.مثلا مثالهای زیر(همگی درستند)ولی نمی دونم به چه دلیل.اگه میشه برام توضیحشون بدین.
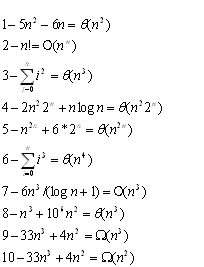
نمی دونم چطور با تحلیل به این نتایج برسم.مثلا واسه به دست آوردن o,w می دونم که باید lim بگیرم.به این صورت:
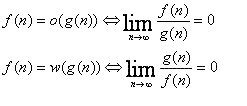
ولی واسه به دست آوردن O, Ω,θ نمی دونم چیکار کنم؟راستی به Ω چی می گین.چون دارم کتاب مقسمی رو می خونم فک کنم اسمشو اشتباه نوشته.
باتشکر.
خواهش می کنم جواب بدین.خداییش این فرمولارو تو ورد نوشتم بعد رفتم به عکس تبدیل کردم بعد آپلود و... اگه هم بلد نیستید برید یادبگیرید بعد به من هم یاد بدید.قبلا از همه تشکر می کنم.من آخر باید O,o,w,Ω,θ رو یاد بگیرم.غیرتی شدم. عکسهارو به ترتیب در ضمیمه قراردادم.
عکسهارو به ترتیب در ضمیمه قراردادم.
من در به دست آوردن مرتبه اجرایی مشکل دارم.مثلا تعاریف O,o,w,Ω,θ رو خوندم ولی نمی دونم چطور در مسائل ازشون استفاده کنم.مثلا مثالهای زیر(همگی درستند)ولی نمی دونم به چه دلیل.اگه میشه برام توضیحشون بدین.
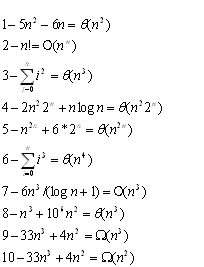
نمی دونم چطور با تحلیل به این نتایج برسم.مثلا واسه به دست آوردن o,w می دونم که باید lim بگیرم.به این صورت:
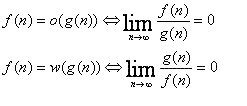
ولی واسه به دست آوردن O, Ω,θ نمی دونم چیکار کنم؟راستی به Ω چی می گین.چون دارم کتاب مقسمی رو می خونم فک کنم اسمشو اشتباه نوشته.
باتشکر.
خواهش می کنم جواب بدین.خداییش این فرمولارو تو ورد نوشتم بعد رفتم به عکس تبدیل کردم بعد آپلود و... اگه هم بلد نیستید برید یادبگیرید بعد به من هم یاد بدید.قبلا از همه تشکر می کنم.من آخر باید O,o,w,Ω,θ رو یاد بگیرم.غیرتی شدم.
 عکسهارو به ترتیب در ضمیمه قراردادم.
عکسهارو به ترتیب در ضمیمه قراردادم.
۱
ارسال: #۲
بدست آوردن O,o,w,Ω,θ در مسائ
در بدست اوردن مرتبه توابع جند جمله ای که راحت ترین کار اینه که برزگنرین مرنبه رو بعنوان مرتبه توابع در نظر بگبریم.
۵n+3logn+10nlogn+7n^2=,θ(n^2
اگه بحوایم مرحله به مرحله پیش بریم میگیم:
۷n^2= θ(n^2
۵n+7n^2=θ(n^ 2 چون رشد n^2 از n بیشتره (تو لیست نرنیب رشدشون رو نوشتم)
۵n+7n^2+3logn=θ(n^ 2^ باز بهمون دلیل
۵n+7n^2+3logn+10nlogn=θ(n^ 2
پس میشه بیشنرین مرتبه ای که در چند چمله ای وحود دارد.
البته به چیز دیگه ای که میتونه بهتون کمک کته اینه:البته منطورم در محاوره است
O به معنی سقف واسه تابع
Ω به مغنی کف تابع
در نظر بگیرید.حالا به توحه به اینکه
, و اونی که سمت راست نابع باشه O نابع میتونه باشه مثلا: n=O(nlogn
که اگر ازش حد هم بگیریم داریم
lim nlogn/n وفتی n به بینهایت میره میشه بینهایت.
امیدوارم منظورم رو رسونده باشم.
۵n+3logn+10nlogn+7n^2=,θ(n^2
اگه بحوایم مرحله به مرحله پیش بریم میگیم:
۷n^2= θ(n^2
۵n+7n^2=θ(n^ 2 چون رشد n^2 از n بیشتره (تو لیست نرنیب رشدشون رو نوشتم)
۵n+7n^2+3logn=θ(n^ 2^ باز بهمون دلیل
۵n+7n^2+3logn+10nlogn=θ(n^ 2
پس میشه بیشنرین مرتبه ای که در چند چمله ای وحود دارد.
البته به چیز دیگه ای که میتونه بهتون کمک کته اینه:البته منطورم در محاوره است
O به معنی سقف واسه تابع
Ω به مغنی کف تابع
در نظر بگیرید.حالا به توحه به اینکه
logn n nlogn n^2 n^i n^k a^n b^n (n!) n^n
از چپ به راست رشدشون سریعتر میشه راحتر میتونید بگید اونهایی که در سمت چپ تابع هستن میتونن Ω اون تابع یاشن.مثلا: (n=Ω(logn, و اونی که سمت راست نابع باشه O نابع میتونه باشه مثلا: n=O(nlogn
که اگر ازش حد هم بگیریم داریم
lim nlogn/n وفتی n به بینهایت میره میشه بینهایت.
امیدوارم منظورم رو رسونده باشم.
ارسال: #۳
RE: بدست آوردن O,o,w,Ω,θ در مسائ
(۱۱ مهر ۱۳۸۹ ۰۵:۰۲ ب.ظ)jaroon نوشته شده توسط: حالا به توحه به اینکهیه چیزی هم من اضافه کنم!
logn n nlogn n^2 n^i n^k a^n b^n (n!) n^nاز چپ به راست رشدشون سریعتر میشه راحتر میتونید بگید اونهایی که در سمت چپ تابع هستن میتونن Ω اون تابع یاشن.مثلا: (n=Ω(logn
, و اونی که سمت راست نابع باشه O نابع میتونه باشه مثلا: n=O(nlogn
که اگر ازش حد هم بگیریم داریم
lim nlogn/n وفتی n به بینهایت میره میشه بینهایت.
امیدوارم منظورم رو رسونده باشم.
اونایه که سمت چپش هستن + خودش میشه( Ω (big-omega. اونایی که فقط سمت چپشن میشه:w
همین طور هم برای سمت راستش.
{اگه احیانا اشتباه می گم لطفا اصلاح کنید}
و اینم میشه تتا:
کد:
θ(f(n)=O(f(n) )n Ω(f(n)) an اینجا یعنی اشتراک! از a هم برای نوشتار درست استفاده کردم و هیچ ربطی به فرمول نداره!!!
نقل قول: تعاریف سوری یکم فهمیدنشون سخته، تو کتاب مقسمی همه این علائم به علامت های > و >= و < و ... ربط داده شده اند که راحتتر میشه اونارو فهمید
تعریف با این علامتها اصلا درست نیست! هیچ فرفی نمی که که توی تعریف مثلا Big o از < استفاده کنیم یا <=! تفاوت اصلی تعریف در سور هایی هست که استفاده شده
برای big-Omega و big O ما از "وجود دارد c که ... " استفاده می کنیم ولی برای small-Omega و small_O از "برای هر C که ..." استفاده می کنیم!
اگه خوب منظورم رو نرسوندم بگین این قسمت رو کاملتر با تعاریفش بگم!
۱
ارسال: #۴
O,o
small o:
باید برای همه مقادیر c جواب بده
اما در Big O یافتن فقط یک مورد هم کافیه .
نتیجه:
O [/code]زیر مجموعه ای از o می باشد.[code]
باید برای همه مقادیر c جواب بده
اما در Big O یافتن فقط یک مورد هم کافیه .
نتیجه:
O [/code]زیر مجموعه ای از o می باشد.[code]
۰
ارسال: #۵
بدست آوردن O,o,w,Ω,θ در مسائل
در مورد شکل اول:
تو چند جمله ایها چند جمله ای از order بزرگترین جمله هستن که از این ده تا خیلی هاشون اینطورین
سومی که به صورت سیگما هستش باید بسط داده بشه که اینطوری میشه: n(n+1)(2n+1)/6 که اگه ضرب کنید از درجه سه هستش، ششمی هم مثل همین باید بسط داده بشه
در مورد دومی n!=O(n^n) سرعت رشد n^n از فاکتوریل بیشتره
فکر میکنم با مراجعه به یه کتاب کنکور یا مرجع میشه کل این مطالبو حل کرد
عکس دوم هم نکته هایی هستن که از کتابهای مرجع یا کنکوری میشه فهمید،در مورد شکل دوم من اینطوری توضیح میدم:
در مورد اولی سرعت رشد g(n) بیشتر از f(n) هستش پس وقتی حد مورد نظر به بینهایت میل میکنه برابر صفر میشه
در مورد دومی هم همینطوریه ولی بصورت بلعکس یعنی سرعت رشد f(n) بیشتره
تو چند جمله ایها چند جمله ای از order بزرگترین جمله هستن که از این ده تا خیلی هاشون اینطورین
سومی که به صورت سیگما هستش باید بسط داده بشه که اینطوری میشه: n(n+1)(2n+1)/6 که اگه ضرب کنید از درجه سه هستش، ششمی هم مثل همین باید بسط داده بشه
در مورد دومی n!=O(n^n) سرعت رشد n^n از فاکتوریل بیشتره
فکر میکنم با مراجعه به یه کتاب کنکور یا مرجع میشه کل این مطالبو حل کرد
عکس دوم هم نکته هایی هستن که از کتابهای مرجع یا کنکوری میشه فهمید،در مورد شکل دوم من اینطوری توضیح میدم:
در مورد اولی سرعت رشد g(n) بیشتر از f(n) هستش پس وقتی حد مورد نظر به بینهایت میل میکنه برابر صفر میشه
در مورد دومی هم همینطوریه ولی بصورت بلعکس یعنی سرعت رشد f(n) بیشتره
۰
ارسال: #۶
RE: بدست آوردن O,o,w,Ω,θ در مسائل
برای تفاوت o ,O ,w,Ω.اگر f(x)=o(g(x))1 حتما متعلق به O(g(x))1 هم خواهد بود .برایw,Ω هم همین تعریف وجود دارد
۰
ارسال: #۷
RE: بدست آوردن O,o,w,Ω,θ در مسائل
اشکال این استدلال چیه؟ کسی میدونه
[tex]\sum_{i=1}^{n}i=1+2+...+n\in O(1+2+...+n)=O(max(1,2,...,n))=O(n)[/tex]
[tex]\sum_{i=1}^{n}i=1+2+...+n\in O(1+2+...+n)=O(max(1,2,...,n))=O(n)[/tex]
ارسال: #۸
RE: بدست آوردن O,o,w,Ω,θ در مسائل
(۱۱ مهر ۱۳۸۹ ۰۹:۰۵ ب.ظ)lucifer نوشته شده توسط: اشکال این استدلال چیه؟ کسی میدونه
[tex]\sum_{i=1}^{n}i=1+2+...+n\in O(1+2+...+n)=O(max(1,2,...,n))=O(n)[/tex]
ببین برای سریها یه فرمول وجود داره به این شکل:
کد:
sigma f(k)= θ( integral 1 to n f(x)dx ) aارسال: #۹
RE: بدست آوردن O,o,w,Ω,θ در مسائل
(۱۱ مهر ۱۳۸۹ ۰۹:۰۵ ب.ظ)lucifer نوشته شده توسط: اشکال این استدلال چیه؟ کسی میدونه
[tex]\sum_{i=1}^{n}i=1+2+...+n\in O(1+2+...+n)=O(max(1,2,...,n))=O(n)[/tex]
اشکال این نوع استدلال در این است که این رابطه در حالتی برقرار است که تعداد توابع یا جملاتی که با هم جمع میشوند ثابت باشد نه متغیر.مثلا در رابطه شما اگر n ثابت بود می توانستید بدین صورتی که نوشتید به جواب برسید.
(۱۱ مهر ۱۳۸۹ ۱۱:۲۱ ب.ظ)karostami نوشته شده توسط: O(1+2+...+n)=O(max(1,2,...,n) غلط است. مجموع ۱ تا n با بیشینه شان برابر نیست. و O شان نیز برابر نخواهد بود. در واقع رشد مجموع این اعداد از رشد ماکسیمم بیشتر است.
یعنی شما میگید که در مجموع ۱ تا n با جملات با بیشینه و O برابر مشکلی برای اینجور حل کردن نیست؟!
مثال زیر هم جملات یکسانه و O اونها هم یکسانه ولی باز هم ماکزیمم گیری غلط است:
[tex]\sum_{i=1}^{n}1=1+1+...+1\in O(1+1+...+1)=O(max(1,1,...,1))=O(1)[/tex]
یا میگید باید مجموع با بیشینه برابر باشه.مثال زیرم مجموع با بیشینه برابر نیست ولی رابطه درسته:
[tex]n+n^{2}\neq max(n,n^{2})[/tex]
[tex]n+n^{2}\in O\left ( n+n^{2} \right )=O(max(n,n^{2}))=O(n^{2})[/tex]
۰
ارسال: #۱۰
بدست آوردن O,o,w,Ω,θ در مسائل
این سری میشه n(n+1)/2 که پیچیدگی زمانی اون O(n^2) هستش، زیاد نمیتونم تایپ کنم 

۰
ارسال: #۱۱
بدست آوردن O,o,w,Ω,θ در مسائل
O(1+2+...+n)=O(max(1,2,...,n) غلط است. مجموع ۱ تا n با بیشینه شان برابر نیست. و O شان نیز برابر نخواهد بود. در واقع رشد مجموع این اعداد از رشد ماکسیمم بیشتر است.
سعی می کنم چند نمونه را توضیح بدهم:
در تابع تتا، در واقع تابعی را می خواهیم که هم رشد با تابع پرسش باشد. برای این کار معمولا از حد بی نهایت استفاده می کنیم. وقتی از یک تابع حد بی نهایت می گیریم، تنها جمله ای که بیشترین توان را دارد اهمیت دارد و بقیه جملات در بینهایت ناچیز هستند یعنی در پرسش اول n^2 تابعی است که هم رشد باتابع است. این تابع هم امگا بیگ و هم او بیگ است. در واقع وقتی شما تتای یک تابع را به دست بیاورید او بیگ و امگا بیگ آنرا نیز به دست آورده اید. ولی این نزدیک ترین خواهد بود برای مثال در همین پرسش n^3 یک او یگ دیگر است. یعنی هر تابعی که رشدش بیشتر از تتا باشد او بیگ تابع پرسش شده هست و هر تابعی که رشدش کمتر و مساوی تتا باشد امگا بیگ نیز هست ولی در امگا کوچک و او کوچک قسمت مساوی وجود ندارد.
در توابع چند جمله ای بهترین روش انتخاب بیشترین توان است.. به دلیل حد بی نهایت تابع.
در تابع دو یعنی n! کافی است این را در نظر داشته باشید که n*(n-1)*(n-2)*...1 از n*n*n...*n کوچکتر است. در اینجا به راحتی نمی توان تتا یا تابعی چندجمله ای که هم رشد با n! باشد را بیابید.
در سوال سوم چنانچه سیگما را بسط بدهید از طریق فرمول های ریاضی به یک چند جمله ای از درجه ۳ خواهید رسید.
در سوال ۴ به این موضوع توجه داشته باشید که رشد لگاریتم از n است.
سوال ۵ نیز یک چندجمله ای است با توان چندجمله ای. اینجا هم تتا برابر است با جمله ای که بیشترین توان را دارد. که اینجا به جای یک عدد ثابت یک چندجمله ای است و لازم است حد بی نهایت آن را در نظر داشته باشید.
و...
(۰۷ مهر ۱۳۸۹ ۰۹:۱۴ ق.ظ)banou نوشته شده توسط: با سلام
من در به دست آوردن مرتبه اجرایی مشکل دارم.مثلا تعاریف O,o,w,Ω,θ رو خوندم ولی نمی دونم چطور در مسائل ازشون استفاده کنم.مثلا مثالهای زیر(همگی درستند)ولی نمی دونم به چه دلیل.اگه میشه برام توضیحشون بدین.
نمی دونم چطور با تحلیل به این نتایج برسم.مثلا واسه به دست آوردن o,w می دونم که باید lim بگیرم.به این صورت:
ولی واسه به دست آوردن O, Ω,θ نمی دونم چیکار کنم؟راستی به Ω چی می گین.چون دارم کتاب مقسمی رو می خونم فک کنم اسمشو اشتباه نوشته.
باتشکر.
خواهش می کنم جواب بدین.خداییش این فرمولارو تو ورد نوشتم بعد رفتم به عکس تبدیل کردم بعد آپلود و... اگه هم بلد نیستید برید یادبگیرید بعد به من هم یاد بدید.قبلا از همه تشکر می کنم.من آخر باید O,o,w,Ω,θ رو یاد بگیرم.غیرتی شدم.عکسهارو به ترتیب در ضمیمه قراردادم.
سعی می کنم چند نمونه را توضیح بدهم:
در تابع تتا، در واقع تابعی را می خواهیم که هم رشد با تابع پرسش باشد. برای این کار معمولا از حد بی نهایت استفاده می کنیم. وقتی از یک تابع حد بی نهایت می گیریم، تنها جمله ای که بیشترین توان را دارد اهمیت دارد و بقیه جملات در بینهایت ناچیز هستند یعنی در پرسش اول n^2 تابعی است که هم رشد باتابع است. این تابع هم امگا بیگ و هم او بیگ است. در واقع وقتی شما تتای یک تابع را به دست بیاورید او بیگ و امگا بیگ آنرا نیز به دست آورده اید. ولی این نزدیک ترین خواهد بود برای مثال در همین پرسش n^3 یک او یگ دیگر است. یعنی هر تابعی که رشدش بیشتر از تتا باشد او بیگ تابع پرسش شده هست و هر تابعی که رشدش کمتر و مساوی تتا باشد امگا بیگ نیز هست ولی در امگا کوچک و او کوچک قسمت مساوی وجود ندارد.
در توابع چند جمله ای بهترین روش انتخاب بیشترین توان است.. به دلیل حد بی نهایت تابع.
در تابع دو یعنی n! کافی است این را در نظر داشته باشید که n*(n-1)*(n-2)*...1 از n*n*n...*n کوچکتر است. در اینجا به راحتی نمی توان تتا یا تابعی چندجمله ای که هم رشد با n! باشد را بیابید.
در سوال سوم چنانچه سیگما را بسط بدهید از طریق فرمول های ریاضی به یک چند جمله ای از درجه ۳ خواهید رسید.
در سوال ۴ به این موضوع توجه داشته باشید که رشد لگاریتم از n است.
سوال ۵ نیز یک چندجمله ای است با توان چندجمله ای. اینجا هم تتا برابر است با جمله ای که بیشترین توان را دارد. که اینجا به جای یک عدد ثابت یک چندجمله ای است و لازم است حد بی نهایت آن را در نظر داشته باشید.
و...
Can I see some ID?
Feeling left out?
نگران نباش، فقط روی این لینک برای ثبت نام کلیک کن. رمزت رو فراموش کردی؟ اینجا به یادت میاریم! close

