۰
subtitle
ارسال: #۱
اشکال در مرتبه زمانی
سلام دوستان مانشتی
لطفا در مورد این سری ها کمکم کنید که در مرتبه زمانی تحلیل الگوریتم های ترتیبی هستش
[tex]1 2 4 ....\begin{matrix}2^{\log n}\end{matrix}=\begin{matrix}2^{\log n 1}\end{matrix}-1=2...\begin{matrix}2\end{matrix}^{\log n}-1=2n-1[/tex]
۲n-1 از کجا اومده
یکی هم این سری
[tex]1^2 2^2 3^2 k^2=\frac{k(k 1)(2k 1)}{6}[/tex]
بچه ها هر کسی میدونه راهنمایی کنه با تشکرررررررر
کسی بلد نبود یکی کمکم کنه خوب راه دور نمیرههههه:

لطفا در مورد این سری ها کمکم کنید که در مرتبه زمانی تحلیل الگوریتم های ترتیبی هستش
[tex]1 2 4 ....\begin{matrix}2^{\log n}\end{matrix}=\begin{matrix}2^{\log n 1}\end{matrix}-1=2...\begin{matrix}2\end{matrix}^{\log n}-1=2n-1[/tex]
۲n-1 از کجا اومده

یکی هم این سری
[tex]1^2 2^2 3^2 k^2=\frac{k(k 1)(2k 1)}{6}[/tex]
بچه ها هر کسی میدونه راهنمایی کنه با تشکرررررررر

کسی بلد نبود یکی کمکم کنه خوب راه دور نمیرههههه:


Aurora، در تاریخ ۰۳ مهر ۱۳۹۴ ۰۳:۴۶ ب.ظ برای این مطلب یک پانوشت گذاشته است:
منتقل شد. لطفا در انتخاب مکان تایپک دقت کنید.
۰
ارسال: #۲
اشکال در مرتبه زمانی
(۰۳ مهر ۱۳۹۴ ۰۱:۵۲ ب.ظ)راحیل۱ نوشته شده توسط: سلام دوستان مانشتی
لطفا در مورد این سری ها کمکم کنید که در مرتبه زمانی تحلیل الگوریتم های ترتیبی هستش
[tex]1 2 4 ....\begin{matrix}2^{\log n}\end{matrix}=\begin{matrix}2^{\log n 1}\end{matrix}-1=2...\begin{matrix}2\end{matrix}^{\log n}-1=2n-1[/tex]
۲n-1 از کجا اومده
یکی هم این سری
[tex]1^2 2^2 3^2 k^2=\frac{k(k 1)(2k 1)}{6}[/tex]
بچه ها هر کسی میدونه راهنمایی کنه با تشکرررررررر
کسی بلد نبود یکی کمکم کنه خوب راه دور نمیرههههه:

سوال دوم هم اثباتش رو نمیدونم تو کتابا معمولا بدون اثبات آورده شده .
ارسال: #۳
RE: اشکال در مرتبه زمانی
(۰۳ مهر ۱۳۹۴ ۰۳:۱۱ ب.ظ)mt95 نوشته شده توسط:(03 مهر ۱۳۹۴ ۰۱:۵۲ ب.ظ)راحیل۱ نوشته شده توسط: سلام دوستان مانشتی
لطفا در مورد این سری ها کمکم کنید که در مرتبه زمانی تحلیل الگوریتم های ترتیبی هستش
[tex]1 2 4 ....\begin{matrix}2^{\log n}\end{matrix}=\begin{matrix}2^{\log n 1}\end{matrix}-1=2...\begin{matrix}2\end{matrix}^{\log n}-1=2n-1[/tex]
۲n-1 از کجا اومده
یکی هم این سری
[tex]1^2 2^2 3^2 k^2=\frac{k(k 1)(2k 1)}{6}[/tex]
بچه ها هر کسی میدونه راهنمایی کنه با تشکرررررررر
کسی بلد نبود یکی کمکم کنه خوب راه دور نمیرههههه:
سوال دوم هم اثباتش رو نمیدونم تو کتابا معمولا بدون اثبات آورده شده .
ممنون از پاسختوننن موفق باشین
این دومی رو هم یکی بگه خوب میشه باتشکر

ارسال: #۴
RE: اشکال در مرتبه زمانی
(۰۳ مهر ۱۳۹۴ ۰۵:۴۴ ب.ظ)راحیل۱ نوشته شده توسط:(03 مهر ۱۳۹۴ ۰۳:۱۱ ب.ظ)mt95 نوشته شده توسط:(03 مهر ۱۳۹۴ ۰۱:۵۲ ب.ظ)راحیل۱ نوشته شده توسط: سلام دوستان مانشتی
لطفا در مورد این سری ها کمکم کنید که در مرتبه زمانی تحلیل الگوریتم های ترتیبی هستش
[tex]1 2 4 ....\begin{matrix}2^{\log n}\end{matrix}=\begin{matrix}2^{\log n 1}\end{matrix}-1=2...\begin{matrix}2\end{matrix}^{\log n}-1=2n-1[/tex]
۲n-1 از کجا اومده
یکی هم این سری
[tex]1^2 2^2 3^2 k^2=\frac{k(k 1)(2k 1)}{6}[/tex]
بچه ها هر کسی میدونه راهنمایی کنه با تشکرررررررر
کسی بلد نبود یکی کمکم کنه خوب راه دور نمیرههههه:
سوال دوم هم اثباتش رو نمیدونم تو کتابا معمولا بدون اثبات آورده شده .
ممنون از پاسختوننن موفق باشین
این دومی رو هم یکی بگه خوب میشه باتشکر
مرسی ابجیه گلمممم
 دست گل هردوتون درد نکنهه
دست گل هردوتون درد نکنهه
ارسال: #۵
RE: اشکال در مرتبه زمانی
(۰۳ مهر ۱۳۹۴ ۰۳:۱۱ ب.ظ)mt95 نوشته شده توسط:(03 مهر ۱۳۹۴ ۰۱:۵۲ ب.ظ)راحیل۱ نوشته شده توسط: سلام دوستان مانشتی
لطفا در مورد این سری ها کمکم کنید که در مرتبه زمانی تحلیل الگوریتم های ترتیبی هستش
[tex]1 2 4 ....\begin{matrix}2^{\log n}\end{matrix}=\begin{matrix}2^{\log n 1}\end{matrix}-1=2...\begin{matrix}2\end{matrix}^{\log n}-1=2n-1[/tex]
۲n-1 از کجا اومده
یکی هم این سری
[tex]1^2 2^2 3^2 k^2=\frac{k(k 1)(2k 1)}{6}[/tex]
بچه ها هر کسی میدونه راهنمایی کنه با تشکرررررررر
کسی بلد نبود یکی کمکم کنه خوب راه دور نمیرههههه:
سوال دوم هم اثباتش رو نمیدونم تو کتابا معمولا بدون اثبات آورده شده .
ببخشید من باز اشکالم تو این که +۱ تو توان log از کجا میادش هنو رفع نشده
 میشه اونجارو بیشتر توضیح بدین
میشه اونجارو بیشتر توضیح بدین
۱
ارسال: #۶
RE: اشکال در مرتبه زمانی
(۰۳ مهر ۱۳۹۴ ۰۱:۵۲ ب.ظ)راحیل۱ نوشته شده توسط: سلام دوستان مانشتی
لطفا در مورد این سری ها کمکم کنید که در مرتبه زمانی تحلیل الگوریتم های ترتیبی هستش
[tex]1 2 4 ....\begin{matrix}2^{\log n}\end{matrix}=\begin{matrix}2^{\log n 1}\end{matrix}-1=2...\begin{matrix}2\end{matrix}^{\log n}-1=2n-1[/tex]
۲n-1 از کجا اومده
یکی هم این سری
[tex]1^2 2^2 3^2 k^2=\frac{k(k 1)(2k 1)}{6}[/tex]
بچه ها هر کسی میدونه راهنمایی کنه با تشکرررررررر
کسی بلد نبود یکی کمکم کنه خوب راه دور نمیرههههه:
والا من از دیشب دارم رو سوالاتون فکر میکنم.
اولی رو پیدا کرده بودم و میخواستم با هم ارسالش کنم که دوستمون حل کردن و نیازی نیس به جواب دادن من
اما دومی:
اگه مبهم یا ناخوانا بود بفرمایید که بهتر توضیح بدم.
![[تصویر: 385750_userupload_2013_970690641443188213.1773.jpg]](https://img.manesht.ir/385750_userupload_2013_970690641443188213.1773.jpg)
![[تصویر: 385750_userupload_2013_19699140181443188322.1811.jpg]](https://img.manesht.ir/385750_userupload_2013_19699140181443188322.1811.jpg)
۰
ارسال: #۷
اشکال در مرتبه زمانی
(۰۳ مهر ۱۳۹۴ ۱۱:۵۰ ب.ظ)راحیل۱ نوشته شده توسط:(03 مهر ۱۳۹۴ ۰۳:۱۱ ب.ظ)mt95 نوشته شده توسط:(03 مهر ۱۳۹۴ ۰۱:۵۲ ب.ظ)راحیل۱ نوشته شده توسط: سلام دوستان مانشتی
لطفا در مورد این سری ها کمکم کنید که در مرتبه زمانی تحلیل الگوریتم های ترتیبی هستش
[tex]1 2 4 ....\begin{matrix}2^{\log n}\end{matrix}=\begin{matrix}2^{\log n 1}\end{matrix}-1=2...\begin{matrix}2\end{matrix}^{\log n}-1=2n-1[/tex]
۲n-1 از کجا اومده
یکی هم این سری
[tex]1^2 2^2 3^2 k^2=\frac{k(k 1)(2k 1)}{6}[/tex]
بچه ها هر کسی میدونه راهنمایی کنه با تشکرررررررر
کسی بلد نبود یکی کمکم کنه خوب راه دور نمیرههههه:
سوال دوم هم اثباتش رو نمیدونم تو کتابا معمولا بدون اثبات آورده شده .
ببخشید من باز اشکالم تو این که +۱ تو توان log از کجا میادش هنو رفع نشدهمیشه اونجارو بیشتر توضیح بدین
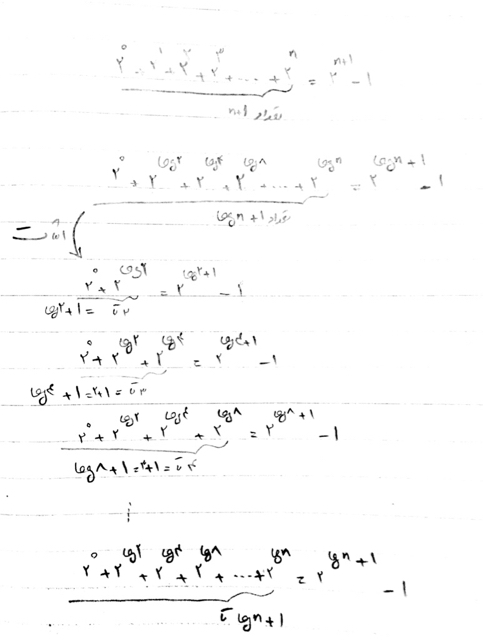
رابطه منطقی بین تعداد وتوان وجود داره که تو شکل نشون دادم و با استقرا ثابت میشه که تعداد اعداد این سری lg n +1 است
Can I see some ID?
Feeling left out?
نگران نباش، فقط روی این لینک برای ثبت نام کلیک کن. رمزت رو فراموش کردی؟ اینجا به یادت میاریم! close


