چرا شما همش نصف می کنید؟ در حالی که باید به اندازه های r1,r2,...rn برش بزنید.
من به راه حل حریصانه فکر کردم...

نه گفته که هزینه برش برابر طول تیر چوبی هست پس ما در هر مرحله باید طول تیر رو حداقل کنیم تا هزینه حداقل بشه!
اینطور نیست؟
اما یه جورایی هم درسته چون از راه حریصانه هم میشه حلش کرد.

نمی دونم ... کسی نظری نداره ؟؟

گویا کسی دوست نداره به من کمک کنه

نه دوست من شما همه رو به شک انداختید

شما استدلالتون رو بفرمایید من این تاپیک رو واسه همین درست کردم که هر کس استدلال خودش رو مطرح کنه. من نظرم اون بوده شما شاید نظرتون متفاوت باشه و البته درست تر از من!!

سلام .
اولا بهتون تبریک میگم چون تست ها رو با استدلال میزنید این خیلی نکته ی مثبتی است .
دوما جوابی که شما دادید در این مورد اشتباه است و هزینه بهینه رو نداره .
البته فک کنم یه مقدار صورت تست رو اشتباه درک کردید شما دارید فقط رو هزینه ی زمانی مسئله مانور میدید در حالی که اصل صورت تست رو فراموش کردید .

***ابتدا باید دنبال راه حل بهینه کمترین هزینه برش چوب ها باشیم بعد دنبال الگوریتمی با کمترین هزینه زمانی باشیم

با یه مثال پیش میریم .
فرض کنید تیر چوبی زیر رو با طول L=10 داریم که حاوی سه نقطه {x1,x2,x3} می باشد




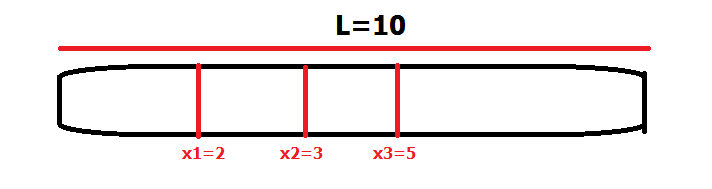
اگر با روش یافتن میانه و سپس پارتیشن این میانه جلو بریم (البته فک کنم پارتیشن هم نمیخوایم چون خود نقاط به ترتیب فاصله از سر چوب قرار دارن که مرتب هستن) هزینه برش به صورت زیر میباشد :
به ترتیب اول نقطه ی x2 بعد نقاط x1,x3 برش میخورن که با توجه به تیکه تیکه شدن هر قسمت در هر مرحله هزینه به صورت زیر میباشد


می بینیم که هزینه برش این تیر با روش یافتن میانه برابر ۲۰ شد .
حالا در ادامه به ترتیب زیر نقاط رو برش میزنیم


میبینیم که این ترتیب برش زدن هزینه بهینه ۱۸ رو به دست آورد که اثبات رد روش شما است .

حالا باید ببینیم تفاوت چیست ؟ در واقع شما احتمال انتخاب یه نقطه رو با استفاده از یک درخت دودویی تقریبا متوازن انجام میدید ، به این ترتیب که میانه در ریشه درخت قرار میگیره و بقیه نقاط در دو طرف که هزینه رسیدن به این نقطه (ریشه) نسبت بقیه نقطه ها بیشتر است و یعنی شما شانسی به بقیه نقاط برای انتخاب در مرحله اول نمیدهید .
حال اگر از تابع احتمالی استفاده کنیم که مثلا برای این مثالی که زدیم شانس رو به نقطه x3 بدهد که در ریشه درخت قرار بگیرد اونوقت به هزینه بهینه میرسیم .
می بینیم روش حل این تست دقیقا تداعی کننده روش درخت جستجوی بهینه است (یافتن احتمال مناسب برای قرار دادن بهترین نقطه در ریشه)

حالا به هزینه روش درخت حستجوی بهینه دقت میکنیم که از مرتبه $\Theta (n^{3})$ است و چند جمله ای

(۱۷ دى ۱۳۹۱ ۰۱:۴۹ ب.ظ)mp1368 نوشته شده توسط:  با یه مثال پیش میریم .
فرض کنید تیر چوبی زیر رو با طول L=10 داریم که حاوی سه نقطه {x1,x2,x3} می باشد



اگر با روش یافتن میانه و سپس پارتیشن این میانه جلو بریم (البته فک کنم پارتیشن هم نمیخوایم چون خود نقاط به ترتیب فاصله از سر چوب قرار دارن که مرتب هستن) هزینه برش به صورت زیر میباشد :
به ترتیب اول نقطه ی x2 بعد نقاط x1,x3 برش میخورن که با توجه به تیکه تیکه شدن هر قسمت در هر مرحله هزینه به صورت زیر میباشد

$X2 = 10$
$X1 = 3$
$X3 = 7$
$10 7 3 = 20$

می بینیم که هزینه برش این تیر با روش یافتن میانه برابر ۲۰ شد .
حالا در ادامه به ترتیب زیر نقاط رو برش میزنیم

$X3= 10$
$X1= 5$
$X2= 3$
$10 5 3 =18$

میبینیم که این ترتیب برش زدن هزینه بهینه ۱۸ رو به دست آورد که اثبات رد روش شما است .

سلام
میبخشید اگه سوالم واضحه از نظر شما ،ولی من متوجه نمیشم شما تو شکلی که کشیدین x2=3 هست پس چرا تو ۲ تا مثال x2=10 گذاشتین؟
همینطور بقیه ی xها
؟
ممنون

اول از این تشکر کنم که شما بعد از ۲ هفته بلاخره اولین کسی هستید که جواب سوالم رو میدید(البته دوستانی بودن که بام همدردی کردند ولی جواب سوالم رو ندادند) .
و بعد هم از تعریفتون بیشتر تشکر میکنم.بله من چون حافظه ی ضعیفی دارم تا مسئله کاملا درک نشه تو ذهنم نمیمونه و باید حتما تجزیه تحلیل کنم.
خوب بریم سراغ جوابی که دادید :
بله استدالتون کاملا صحیح هست.و کاملا هم مشخص !
نه من دنبال مرتبه زمانی نبودم ، فقط دنبال جواب بهینه بودم و انقدر راه حلم بدیهی بود که تو نوشتنش عجله کردم و به اشتباه میانه رو وسط کشیدم(همون لحظه تایپ راه حل رو نوشتم) ، در صورتی که خیلی ساده تر میشه از طریق بازگشتی حلش کرد که بهینه هم باشه!
شما از این نکته به اشتباه افتادید که من گفتم میانه ها و بر اساس اونهم حساب کردم . اما منظورم کلا وسط بود.
خوب حالا راه حل بازگشتی که بر اساس وسط تیر چوبی کار کنه :
میشه جای میانه اینطور فرض کرد که در هر بار نزدیکترین نقطه به وسط تیر چوبی، برش داده میشه به این صورت که ابتدا طول تیر چوبی رو نصف میکنیم و اسمشو m میذاریم و از طریق جستجوی دودویی دنبال نزدیکترین نقطه برش به m میگردیم که با lg n قابل انجامه خوب حالا چوب رو نصف میکنیم و هر نصف رو به صورت بازگشتی دوباره به همین حالت تقسیم میکنیم. حالا مسئله با زمان تقریبا nlg n که بازم چند جمله ایه.
من مشکلم با اثبات روش پویا نبود بلکه من مشکلم با اینه که چرا توی گزینه ها گفته که با بقیه روشهای برنامه نویسی نمیشه پیاده سازیش کرد که شما اگه بخواید من با همه روشها واستون حل میکنم. من میخوام این ثابت بشه ، چرا فقط روش پویا ؟؟؟

من سپاس رو زدم برای دوستمون.
اما خودم یه جا دیگه ثابت کردم میشه O)N
---
لطفا بفرمایید آیا نمونه ی این سوال توی کتابی حل شده است یا خیر؟