برای درخت با ارتفاع n-1 چون که این ارتفاع درخت رو مجبور می کرد که در هر سطح فقط یک عنصر داشته باشه میتونیم با اصل ضرب تعداد کل این درخت‌ها رو به دست بیاریم ولی اینجا چون که با این ارتفاع نمیتونیم مشخصا بگیم که در هر سطح چند عنصر باشه فک نکنم فرمولی داشته باشه.
شایدم با یک راه دیگه بشه بدست آورد

اگر سوال تستی هست گزینه‌ها رو بگید.در غیر اینصورت بدست آوردن فرمول کار ساده ای نیست.بهر حال اولین چیزی که به ذهنم میرسه اینه:
توی حالتی که می خواهیم ارتفاعمون n-1 بشه یک گره توی ریشه(سطح صفر) قرار میگره و n-1 گره دیگه هر کدوم به ترتیب توی سطحهای ۱ تا n-1 باید قرار بگیرند و تمام گره‌ها به غیر از آخری که برگ هست تک فرزندی میشند که هر کدوم دو حالت دارند(فرزند چپ یا راست والد باشند)
حالا اگر تا اینجارو فهمیدید سوال دومتون رو میشه اینطوری تفسیر کرد:
ما نیاز به ارتفاع دقیقا n-3 داریم.پس بیشترین فاصله برگمون از ریشه باید n-3 بشه.یعنی یک زیر درخت با ارتفاع n-3 داریم.پس باید n-3 گره توی عمق قرار بگیرند تا ارتفاعمون n-3 بشه.این n-3 گره هم می تونند فرزند چپ باشند هم فرزند راست.پس تا اینجا ۲ بتوان n-3 تا حالت داشتیم.ریشه هم هم که گذاشتیمش سر جاش و از n تا گره دو تا گره‌ی دیگه مونده که باید یه جایی بزاریمشون.حالا کجا می تونیم بزاریمشون؟ توی اتصالات خالی(به غیر از اتصالات خالی اخرین سطح چونکه اگر گره را اونجا بزاریم ارتفاع درخت از اونی که می خواهیم زیادتر میشه) که میشه تعداد کل اتصالات(۲(n-3)) منهای اتصالات پر(n-3).که میشه:n-3.
ولی اگر من این گره در سطح یکی مونده به اخر بزارم گره‌ی اخر را هم می تونم فرزند اون قرار بدم(سطح آخر) و بازم ارتفاع میریزه بهم! پس یکبار در نظر میگیریم که توی سطح اخر گره را نمی گذاریم و یکبار یک گره را در سطح اخر میگذاریم.
اگر در سطح اخر گره را نگذاریم گره اولو توی n-4 حالت می تونیم بزاریم و گره‌ی بعدیش رو توی n-3 تا(چراکه گره اولو که میزاریم درسته که یک اتصال کم میشه ولی دو تا اتصال به عنوان فرزند چپ و راست اون گره ایجاد میشه و در کل مکانهامون یکی زیاد میشه!)
اگر گره اولو در سطح اخر بگذاریم گره بعدی می تواند در n-4 حالت قرار بگیرد.(در این حالت چون گره اول توی سطح اخر هست نمی تونه فرزند داشته باشه مگرنه ارتفاع درخت بهم می خوره)
پس با این حساب باید جواب یه چیزی توی مایه های (!) دو بتوان n-3 ضربدر( (n-4)(n-3)+(n-4) )بشود ولی نمیشه! چونکه توی اون دو بتوان n-3 حالت خیلی از حالتها با حالت هایی که توی قسمت دو گره بدست اوردیم تکراری در میاد و بعضی حالات دوبار شمرده میشوند! حالا باید حالات تکراری رو بشماریم.اگر کسی تا این قسمتو خونده عجب حوصله ای داشته!!! بگذریم در نهایت یک تقسیم بر دو میکنیم(!) و جواب نهایی میشه:
دو بتوان n-4 ضربدر (n-4)(n-2)
مثلا با ۵ گره میشه ۶ تا درخت با ارتفاع ۲ رسم کرد.(ارتفاع رو از صفر باید بگیرید)
حسابی دری بری گفتم نه؟!!

احیانا منظورتون درخت دودویی نیست؟

(۳۰ آذر ۱۳۸۹ ۰۸:۲۷ ق.ظ)afagh1389 نوشته شده توسط:  احیانا منظورتون درخت دودویی نیست؟

با توجه به جواب سوال اولشون باید درخت دودویی باشه.

(۳۰ آذر ۱۳۸۹ ۰۹:۰۰ ق.ظ)samanium نوشته شده توسط:  در مورد خود درخت هم باید اطلاعاتی بدین
فک کنم n هم باید از ۳ بزرگتر باشه

ارتفاع رو باید از صفر بگیرید چونکه جواب اول را هم بر این اساس دادند.پس n باید بزرگتر مساوی ۵ باشه.



به نظر اساتید این راه که دیشب توی حالت خواب و بیدار(!) نوشتم درسته؟!

در مورد خود درخت هم باید اطلاعاتی بدین
فک کنم n هم باید از ۳ بزرگتر باشه

خوب وقتی میگه به ارتفاع n-1 یعنی درخت اریب حالا وقتی بخوایم از ارتفاعش کم کنیم باید ۲ تا از گره های آخر رو برداریم و بعد n-3 تا گره پدر رو انتخاب کنیم و اون گره‌ها رو جای فرزندشون قرار بدیم چون درخت ما اربیه جای یک فرزند رو بیشتر نداره (فرزند قبلی سر جای خودش هست) پس میشه تعداد حالات ساخت درخت قبلی ضربدر انتخاب ۲ از n-3

حالات اضافه کردن گره‌ها میشه n-3*n-4/2 جواب آخر از نظر من میشه دو به توان n-2 ضرب در n-3*n-4

---

آقا حامد نمیدونم جواب شما هم همین بود یا نه؟!
فقط شما گفتین حالات تکراری پیش میاد اما پیش نمیاد چون فرق داره که نود رو بگذاریم سمت چپ یا راست.
به خاطر همین وقتی درخت اریب به راسته میگذاریم سمت چپ و وقتی اریب به چپه میگذاریم سمت راست { یعنی دستمون بسته است} پس حالت تکراری ایجاد نمیشه.

واژه اریب واژه مناسبی برای این حالت نیست توی اریب ما یا اریب چپ داریم یا اریب راست.ولی توی این مساله لازم نیست همه فرزند چپ باشند یا همه فرزند راست.مهم اینه که والد‌ها تک فرزندی هستند.
چرا دو به توان n-2 ؟ باید دو به توان n-3 باشه.درسته؟
مثلا با ۵ گره می خواهیم درختهایی با ارتفاع ۲ رسم کنیم.۳ تا گره برای ارتفاع دو نیاز داریم که بصورت عمقی قرار بگیرند و ارتفاعشون ۲ بشه.مثلا مثل شکل زیر:


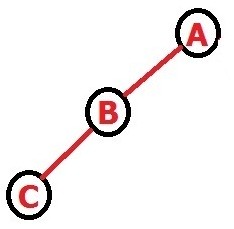
اگر حساب کنید میبینید که توی ۴ حالت می تونند با ارتفاع ۲ قرار بگیرند.(هر دو چپ-هر دو راست-اولی چپ دومی راست-اولی راست دومی چپ) که با فرمول دو به توان n-3 جور در میاد.
حالا روی همون شکل توضیح میدم.دو تا گره‌ی دیگه هم باید قرار بدیم تا تعداد گره هامون بشه ۵ و ارتفاعمون هم نباید عوض بشه.شما میگید دو تا جا(فرزند راست A و فرزند راست B) داریم و حالاتمون می شه ترکیب ۲ از ۲(n-3) ولی اینجا نباید از ترکیب استفاده کنید.اگر من گره‌ی اولو فرزند راست A قرار بدم گره‌ی دوم می تونه فرزند چپ یا راست گره اول باشه.که این حالت رو شما در نظر نمی گیرید.مطابق شکل زیر:


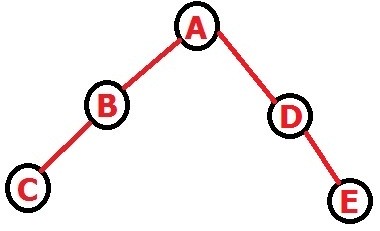
در مورد تکراری ها:من نگفتم توی اون دو به توان n-3 تا تکراری داریم.گفتم ترکیب حالات قبلی با حالات اضافه کردن دو گره حالات تکراری ایجاد میکنه.برگردیم به شکل بالا.توی این حالت من یک اریب چپ در نظر گرفته بودم و دو تا گره(D,E) رو فرزند راست انتخاب کرده بودم.اگر من اریب راست میگرفتم و دو تا گره را فرزند چپ می گرفتم بازم همون شکل بالا ایجاد میشد.
در کل فرمولی که من گفتم برای ۵ تا گره میگه ۶ تا درخت با ارتفاع ۲ وجود دارد که اگر شکل بکشید دقیقا بدین گونه میباشد.۶ درخت مطابق شکل‌ها‌ی زیر:

ممنون متوجه شدم.
حالا آخر جواب چی میشه؟؟

(۳۰ آذر ۱۳۸۹ ۰۲:۲۸ ب.ظ)afagh1389 نوشته شده توسط:  ممنون متوجه شدم.
حالا آخر جواب چی میشه؟؟

به نظر خودم راهم یه جاییش اشتباه داره! یه خورده بی منطق اون قسمت اخر بخاطر تعداد حالات تکراری تقسیم بر دو کردم و شاید برای اعداد بزرگتر جواب غلط بده.
بهر حال کسی همچین سوال هایی رو حل نمی کنه.توی ۴ تا گزینه ۵ میزاریم و می بینیم کدوم ۶ میشه.

آره نمیدونم چرا توی مانشت بچه‌ها تستها رو بدون گزینه و جواب میگذارن؟ شاید میخوان مارو تست کنن!

با سلام خدمت شما دوستان.
در جوابا بود که حالات تکراری ایجاد نمیشه در صورتی که ایجاد میشه.
با n گره چند درخت با ارتفاع n-1 می توان رسم کرد ؟
جواب‌: دو به توان n-1

با n گره چند درخت با ارتفاع n-2 می توان رسم کرد ؟
جواب (دو به توانn-2 )* (n-2)) منهای ۲ به توان n-3
با n گره چند درخت با ارتفاع n-3 می توان رسم کرد ؟
راستی منظور درخت دودویی بوده حالا جواب چیه؟
راستی آقا حامد از کجا میدونی که حالات تکراری بیشتری در گره های بیشتر ایجاد نمیشه؟

(۳۰ آذر ۱۳۸۹ ۰۵:۵۴ ب.ظ)maneshti نوشته شده توسط:  با سلام خدمت شما دوستان.
در جوابا بود که حالات تکراری ایجاد نمیشه در صورتی که ایجاد میشه.
با n گره چند درخت با ارتفاع n-1 می توان رسم کرد ؟
جواب‌: دو به توان n-1

با n گره چند درخت با ارتفاع n-2 می توان رسم کرد ؟
جواب (دو به توانn-2 )* (n-2)) منهای ۲ به توان n-3
با n گره چند درخت با ارتفاع n-3 می توان رسم کرد ؟
راستی منظور درخت دودویی بوده حالا جواب چیه؟
راستی آقا حامد از کجا میدونی که حالات تکراری بیشتری در گره های بیشتر ایجاد نمیشه؟

در جوابی که نوشتید واضحه که حالات تکراری رو ازش کم کرده.
پس رابطه ای رو که نوشتم به صورت زیر تصحیح می نمایم:
با n گره چند درخت با ارتفاع n-3 می توان رسم کرد ؟
دو بتوان n-3 ضربدر (n-4)(n-2) منهای دو بتوان n-4 ضربدر (n-2)
که منها همون حالات تکراریمون هستند.رابطه را برای n=5 و n=6 امتحان کردم.البته نیومدم کل حالات رو برای ۶ تا گره بکشم بلکه حالات تکراری رو کشیدم که دقیقا ۱۶ تا بود.
با این حال ممکنه جایی اشتباهی کرده باشم.توی کدوم کتاب این مطالب رو بیان کرده؟

برای درخت با ارتفاع n-2 اول درختهای با ارتفاع n-2 توسط n-1 گره رو رسم میکنیم. بعد گره آخر رو برمیداریم و به عنوان فرزند n-2 گره دیگه قرار میدیم (چون n-1 فرزند باقی میمونه که خودش یکی از اونها قبلا پدر این گره بوده) پس میشه n-2*2^n-2
بعد حالات تکراری رو ازش کم میکنیم.(دو به توان n-2 تقسیم بر ۲)

این سوال رو استادمون مطرح کرده بود

---

با n گره چند درخت با ارتفاع n-3 می توان رسم کرد ؟

آقا حامد یه لطف میکنی توضیح بدی چرا اینجوری شد؟وجواب این شد؟

(۰۴ دى ۱۳۸۹ ۱۰:۱۸ ق.ظ)maneshti نوشته شده توسط:  آقا حامد یه لطف میکنی توضیح بدی چرا اینجوری شد؟وجواب این شد؟

نگفتید که کدوم قسمتشو میتوجه نشدید.
بدست آوردن تعداد حالات رو که توی پست های قبل گفته بودم.فقط حالات تکراری رو که توی پست قبل گفتم عجله داشتم و توضیح ندادم.بهر حال:
اول مساله تعداد درخت با ارتفاع n-2 رو توضیح میدم که به مراتب راحت تره.
از ریشه شروع میکنیم(یک گره) و با n-2 گره به سمت پایین حرکت میکنیم.هر کدوم از این n-2 گره می تونند فرزند چپ یا راست باشند پس تا اینجا دو بتون n-2 حالت داریم.ولی تا اینجا درختمون n-1 گره داره و باید یک گره‌ی دیگر را در مکان مناسبی قرار دهیم.این گره آخر می تونه هر جایی قرار بگیره بجز فرزند اخرین گره(چونکه در اون حالت ارتفاع از n-2 که تنظیم کردیم بیشتر میشه).پس فرزند هر کدوم از این n-1 گره که توی شکل داریم می تونه باشه بجز گره سطح آخر.پس به عنوان فرزند n-2 گره می تونه قرار بگیره.و این N-2 گره هر کدومشون از قبل یک فرزند دارند پس برای هر کدومشون فقط یک حالت وجود داره.پس تا اینجا دو بتوان n-2 ضربدر n-2 حالت داریم.ولی توی این حالات حالات تکراری هم وجود داره.بدین صورت که گره اخر رو که میخواهیم قرار بدیم توی آخرین سطح(فرزند گره یکی مونده به اخر) بزاریم.این حالت می تونه اینطور تعبیر بشه که گره اخر جزیی از همون n-2 گره که برای رسیدن به ارتفاع ازشون کمک گرفتیم بوده و گره دیگری گره اخر بوده است.تعداد حالات توی این مورد برابر میشه با: تعداد حالات رسیدن به سطح یکی مونده به اخر:که ارتفاع درختمون n-1 بود و سطح مورد نظر میشه n-2 پس تعداد حالات تکراری مورد نظر میشه دو بتوان n-2.توجه داشته باشید که گره انتخابی در سطح اخر تنها یک حالت دارد چونکه یکی از فرزندان گره سطح n-2 قبلا پر شده است.
بر میگریم به مساله تعداد درخت با ارتفاع n-2:
قبلا قسمت اولشو به صورت زیر توضیح دادم:

(۳۰ آذر ۱۳۸۹ ۰۱:۱۱ ق.ظ)حامد نوشته شده توسط:  ما نیاز به ارتفاع دقیقا n-3 داریم.پس بیشترین فاصله برگمون از ریشه باید n-3 بشه.یعنی یک زیر درخت با ارتفاع n-3 داریم.پس باید n-3 گره توی عمق قرار بگیرند تا ارتفاعمون n-3 بشه.این n-3 گره هم می تونند فرزند چپ باشند هم فرزند راست.پس تا اینجا ۲ بتوان n-3 تا حالت داشتیم.ریشه هم هم که گذاشتیمش سر جاش و از n تا گره دو تا گره‌ی دیگه مونده که باید یه جایی بزاریمشون.حالا کجا می تونیم بزاریمشون؟ توی اتصالات خالی(به غیر از اتصالات خالی اخرین سطح چونکه اگر گره را اونجا بزاریم ارتفاع درخت از اونی که می خواهیم زیادتر میشه) که میشه تعداد کل اتصالات(۲(n-3)) منهای اتصالات پر(n-3).که میشه:n-3.
ولی اگر من این گره در سطح یکی مونده به اخر بزارم گره‌ی اخر را هم می تونم فرزند اون قرار بدم(سطح آخر) و بازم ارتفاع میریزه بهم! پس یکبار در نظر میگیریم که توی سطح اخر گره را نمی گذاریم و یکبار یک گره را در سطح اخر میگذاریم.
اگر در سطح اخر گره را نگذاریم گره اولو توی n-4 حالت می تونیم بزاریم و گره‌ی بعدیش رو توی n-3 تا(چراکه گره اولو که میزاریم درسته که یک اتصال کم میشه ولی دو تا اتصال به عنوان فرزند چپ و راست اون گره ایجاد میشه و در کل مکانهامون یکی زیاد میشه!)
اگر گره اولو در سطح اخر بگذاریم گره بعدی می تواند در n-4 حالت قرار بگیرد.(در این حالت چون گره اول توی سطح اخر هست نمی تونه فرزند داشته باشه مگرنه ارتفاع درخت بهم می خوره)
پس با این حساب باید جواب یه چیزی توی مایه های (!) دو بتوان n-3 ضربدر( (n-4)(n-3)+(n-4) )بشود ولی نمیشه! چونکه توی اون دو بتوان n-3 حالت خیلی از حالتها با حالت هایی که توی قسمت دو گره بدست اوردیم تکراری در میاد و بعضی حالات دوبار شمرده میشوند! حالا باید حالات تکراری رو بشماریم.

برای حالات تکراری:
موقعی حالت تکراری بوجود می آید که دو گره انتخابی من جزوی از اون n-3 گره اولیه حساب بشوند.حالا می تونه یکی از این دو گره توی همچین حالتی قرار بگیره یا هر دوی اونها.پس دو حالت کاملا مجزا را باید بدست بیاریم و از تعداد حالاتی که قبلا بدست آوردیم کم کنیم:
۱/یکی از دو گره به عنوان بخشی از اون N-3 گره تعبیر بشه:
تعداد حالات برابر میشه با:تعداد حالات رسیدن به ارتفاع n-4 ضربدر تعداد حالات قرار دادن دو گره.قسمت اولشو که واضحه میشه دو بتونا n-4.یکی از دو گره هم باید به ارتفاع N-3 برسه که مجبور توی یک حالت قرار بگیره(فرزند گره سطح n-4 ). گره دیگر هم باید جایی بزاریم که برای ارتفاعمون مشکل ساز نشه که n-4 حالت داره(در قسمتهای قبلی توضیح داده شد).تعداد حالات برابر میشه با: دو بتون n-4 ضربدر n-4
۲/هر دو گره به عنوان بخشی از اون N-3 گره تعبیر بشه:تعداد حالات برابر میشه با:تعداد حالات رسیدن به ارتفاع n-5 ضربدر تعداد حالات قرار دادن دو گره.قسمت اولشو که واضحه میشه دو بتونا n-5.دو گره باقی مونده باید توی عمق پیش برند و برسند به سطح n-3.گره اول در یک حالت به عنوان فرزند باقی مونده گره سطح n-5 قرار میگیره و گره دو در دو حالت به عنوان فرزند گره اون قرار میگیره.از طرفی برای فرزندان طرف دیگر گره n-5 نیز به طور مشابه دو حالت پیش می آید.تعداد حالات برابر میشه با: دو بتون n-5 ضربدر ۴/
تعدا حالات نهایی برابر است با:
دو بتوان n-3 ضربدر( (n-4)(n-3)+(n-4) منهای دو بتون n-4 ضربدر n-4 منهای دو بتون n-5 ضربدر ۴/
بعد از ساده سازی:
دو بتوان n-3 ضربدر(n-4)(n-2) منهای دو بتون n-4 ضربدر n-2.

فکر کنم برای ارتفاع n-1 ریشه در ارتفاع ۱قرار میگیره و بقیه گره هاکه n-1 تاهست میتونن تو زیردرخت چپ قراربگیرن یا راست پس هرکدام دوحالت دارن.پس میشه دو ب توانn_1.دومی هم یه کم فکر میخاد.شمااگه جوابوداری بزار ببینیم میتونیم بهش برسیم یانه.