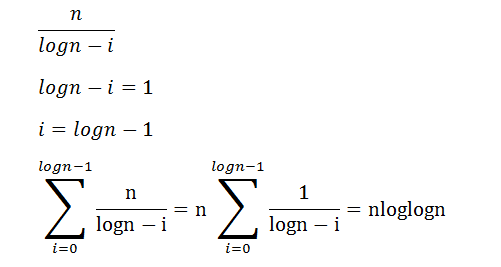۰
subtitle
ارسال: #۱
یه سوال بازگشتی از قضیه اصلی
این رابطه بازگشتی رو کسی میتونه حل کنه؟
[tex]T(n)=2T(\frac{n}{2}) \frac{n}{logn}[/tex]
مسئله من زانی هست که درختشو رسم می کنم.
مسئله های دیگه راحت میشه تعیین کردن مقدار i یا بعبارتی ارتفاع درخت چنده.
اینو نمی دونم چطوری باید تعیین کنم
هر راه حلی هم که نگاه کردم همشون کپی هم بودن و من چیزی دستگیرم نشد...
[tex]T(n)=2T(\frac{n}{2}) \frac{n}{logn}[/tex]
مسئله من زانی هست که درختشو رسم می کنم.
مسئله های دیگه راحت میشه تعیین کردن مقدار i یا بعبارتی ارتفاع درخت چنده.
اینو نمی دونم چطوری باید تعیین کنم
هر راه حلی هم که نگاه کردم همشون کپی هم بودن و من چیزی دستگیرم نشد...

۰
ارسال: #۳
RE: یه سوال بازگشتی از قضیه اصلی
۰
ارسال: #۴
RE: یه سوال بازگشتی از قضیه اصلی
من نمی دونم مشکلتون کجاست درخت رو کشیدم وضمیمه می کنم ارتفاع درخت هم lgn است
که از روی درخت روابط زیر رو داریم
[tex]\frac{n}{lgn} \frac{n}{lgn-1} \frac{n}{lgn-2} ...=n(\frac{1}{lgn} \frac{1}{lgn-1} \frac{1}{lgn-2} ...)=nlglgn[/tex]
که از روی درخت روابط زیر رو داریم
[tex]\frac{n}{lgn} \frac{n}{lgn-1} \frac{n}{lgn-2} ...=n(\frac{1}{lgn} \frac{1}{lgn-1} \frac{1}{lgn-2} ...)=nlglgn[/tex]
۰
ارسال: #۵
RE: یه سوال بازگشتی از قضیه اصلی
ببینید مسئله من اینجاس که اگر قرار باشه [tex]\frac{n}{logn-i}[/tex] رو برابر یک قرار بدهیم.
پس i چطوری حساب میشه؟
پس i چطوری حساب میشه؟
۰
ارسال: #۶
یه سوال بازگشتی از قضیه اصلی
برای یافتن ارتفاع درخت شما باید عبارت داخل پرانتز جلوی T رو پس از i مرحله مساوی یک بگذارید.
یعنی [tex]\LARG \frac{n}{2^{i}}=1\rightarrow i=Log n[/tex]
(البته من سطح ریشه رو صفر فرض کردم)
--------------------------------------------------------------------------------------------
اون جوابی هم که دوستمون ahmadnouri داده اند در واقع همان جمع هزینه های سطوح درخت می باشد که هدف ما هم همینه.
و من هم تایید می کنم.
یعنی [tex]\LARG \frac{n}{2^{i}}=1\rightarrow i=Log n[/tex]
(البته من سطح ریشه رو صفر فرض کردم)
--------------------------------------------------------------------------------------------
اون جوابی هم که دوستمون ahmadnouri داده اند در واقع همان جمع هزینه های سطوح درخت می باشد که هدف ما هم همینه.
و من هم تایید می کنم.
۰
ارسال: #۷
RE: یه سوال بازگشتی از قضیه اصلی
متوجه شدم: 
ببینید داریم:
[tex]\frac{n}{2^{i}}=1[/tex]
[tex]i = logn[/tex]
[tex]\sum_{i=0}^{logn-1}\frac{n}{logn-i}[/tex]
حالا علت اینکه سیگما تا logn-1 هستش اینه که اگه تا logn باشه مخرج کسر صفر میشه و کسر تعریف نشده خواهد بود

ببینید داریم:
[tex]\frac{n}{2^{i}}=1[/tex]
[tex]i = logn[/tex]
[tex]\sum_{i=0}^{logn-1}\frac{n}{logn-i}[/tex]
حالا علت اینکه سیگما تا logn-1 هستش اینه که اگه تا logn باشه مخرج کسر صفر میشه و کسر تعریف نشده خواهد بود

ارسال: #۸
RE: یه سوال بازگشتی از قضیه اصلی
(۰۲ آبان ۱۳۹۰ ۰۹:۵۲ ب.ظ)پشتکار نوشته شده توسط: متوجه شدم:
ببینید داریم:
[tex]\frac{n}{2^{i}}=1[/tex]
[tex]i = logn[/tex]
[tex]\sum_{i=1}^{logn-1}\frac{n}{logn-i}[/tex]
حالا علت اینکه سیگما تا logn-1 هستش اینه که اگه تا logn باشه مخرج کسر صفر میشه و کسر تعریف نشده خواهد بود
روی سیکما i از صفر شروع می شه نه از یک.( سطح ریشه صفره)
در مورد اون "منهای یک" که در Lgn -1 بالای سیکما هستش هم فکر می کنم باید دلیل بهتری (یک دلیل ساختمان داده ای) برای اومدنش داشته باشه.
چون بازهی سیکما باید از i=0 (سطح صفرم) تا سطح آخر( یعنی i )باشه و i هم مساوی Log n هستش.
Can I see some ID?
Feeling left out?
نگران نباش، فقط روی این لینک برای ثبت نام کلیک کن. رمزت رو فراموش کردی؟ اینجا به یادت میاریم! close