۰
subtitle
ارسال: #۱
Np hard فناوری اطلاعات ۹۵
سلام دوستان خسته نباشید سوالم اینه
مسائل p در زمان چند جمله ای حل میشن
مسائل NP هم در زمان چند جمله ای به صورت نامعین حل میشن
از طرفی توی تعریف کتاب پوران مسائل بغرنج در زمان چندجمله ای حل نمیشن مثل کوله پشتی صفر و یک و فروشنده دوره گرد
حالا سوالم اینه جدای از تعریفای NP-hard و NP-complete یه مساله باید چه پیچیدگی زمانی داشته باشه که تو اون دسته باشه؟!!!
مثلا سوال زیر تو سنجش زده گزینه یک چرا؟
بعد یه سوال دیگه کلمه بغرنج یعنی چی؟ وقتی میگه تو زمان بیشتر از چندجمله ای باشه مسئله بغرنجه یعنی np-hard یا np-complete هست؟

مسائل p در زمان چند جمله ای حل میشن
مسائل NP هم در زمان چند جمله ای به صورت نامعین حل میشن
از طرفی توی تعریف کتاب پوران مسائل بغرنج در زمان چندجمله ای حل نمیشن مثل کوله پشتی صفر و یک و فروشنده دوره گرد
حالا سوالم اینه جدای از تعریفای NP-hard و NP-complete یه مساله باید چه پیچیدگی زمانی داشته باشه که تو اون دسته باشه؟!!!
مثلا سوال زیر تو سنجش زده گزینه یک چرا؟
بعد یه سوال دیگه کلمه بغرنج یعنی چی؟ وقتی میگه تو زمان بیشتر از چندجمله ای باشه مسئله بغرنجه یعنی np-hard یا np-complete هست؟

۱
ارسال: #۲
RE: Np hard فناوری اطلاعات ۹۵
سلام و وقت بخیر ... دوست داشتم که یک جا این تعاریف رو این دمه کنکوری خدمتتون عرض کنم که واسه خودم هم یه مروری بشه ...
کلاس P = مسائلی که برای حل آنها الگوریتم یا الگوریتمهایی با مرتبه زمانی چندجملهای یافت شده است کلاس الگوریتمهای معین یا الگوریتمهای قطعی را تشکیل میدهند. این کلاس را با علامت ویژه p که کوتاه شده polynomial به معنای چندجملهای هست نمایش میدهیم.
کلاس NP = باید در زمان چندجملهای با استفاده از یک ماشین قطعی تورینگ قابل تصدیق شدن باشند. در تعریفی مشابه گفته میشود که NP مجموعهی مسائل تصمیمگیری است که در زمان چندجملهای و با استفاده از ماشین غیرقطعی تورینگ قابلحل شدن هستند. کلاس پیچیدگی P یکی از اعضای NP است
کلاس NP-Complete = مسایلی که برای آنها هیچ الگوریتم شناخته شده قابل اجرا در زمان چند جمله ای وجود ندارد .
کلاس NP-Hard = به معنای حل نشدنی درزمان چندجملهای بر حسب اندازهٔ ورودی مساله (زمان معقول)
معروفترین مسائل ان پی-سخت: ۱- مسئله فروشنده دورهگرد ۲- مسئله بزرگترین خوشه (پیدا کردن بزرگترین زیرگراف کامل)
برای آنکه مسئلهای Intractable یا بغرنج باشد باید اثبات کرد که هیچ الگوریتمی با مرتبه چندجملهای برای آن وجود ندارد. ازنظر بغرنج بودن یا نبودن، مسائل علوم کامپیوتر سه دسته هستند:
۱- مسائلی که الگوریتمهایی با پیچیدگی زمانی چندجملهای برای آنها پیداشده است.
۲- مسائلی که اثباتشده است که بغرنج هستند، یعنی الگوریتم چندجملهای برای آن یافت نمیشود.
۳- مسائلی که بغرنج بودن آنها ثابت نشده است ولی از طرف دیگر هیچ الگوریتم چندجملهای هم برای آنها پیدا نشده است.
مثلاً جستوجوی دودویی در آرایه مرتب با مرتبه زمانی [tex]\theta(\lg n)[/tex] ، مسئله مرتبسازی آرایهها با مرتبه زمانی [tex]\theta(nlgn)[/tex] ، ضرب زنجیرهای ماتریسها با مرتبه زمانی [tex]\theta(n^3)[/tex] از دسته اول هستند. همچنین مسائل کوتاهترین مسیر فلوید با مرتبه زمانی [tex]\theta(n^3)[/tex]، درخت دودویی بهینه [tex]\theta(n^3)[/tex] و مسئله درخت پوشای کمینه پریم [tex]\theta(n^2)[/tex]بااینکه الگوریتمهای نمایی نیز دارند ولی چون برای آنها الگوریتمهایی از نوع چندجملهای یافت شده است از این دستهاند.
تعداد مسائلی که جزو دسته دوم بوده و بغرنج بودن آنها اثباتشده است، نسبتاً کم بوده است. نمونهای از این مسائل دسته دوم، حساب پرزبرگر است.
مسئله کولهپشتی صفر و یک و مسئله فروشنده دورهگرد از دسته سوم هستند.
البته دقت شود در این سوال الگوریتمی پویا وجود دارد که از مرتبه [tex]O(NM)[/tex] است ولی این چند جمله ای بر حسب تعداد اشیا نیست این مساله در هر دو حالت ( حالت اول این که از هر شی یک نمونه باشد و حالت دوم از هر نمونه تعداد بی شمار باشد ) از نوع ان پی کامل است در نتیجه ان پی سخت
کلاس P = مسائلی که برای حل آنها الگوریتم یا الگوریتمهایی با مرتبه زمانی چندجملهای یافت شده است کلاس الگوریتمهای معین یا الگوریتمهای قطعی را تشکیل میدهند. این کلاس را با علامت ویژه p که کوتاه شده polynomial به معنای چندجملهای هست نمایش میدهیم.
کلاس NP = باید در زمان چندجملهای با استفاده از یک ماشین قطعی تورینگ قابل تصدیق شدن باشند. در تعریفی مشابه گفته میشود که NP مجموعهی مسائل تصمیمگیری است که در زمان چندجملهای و با استفاده از ماشین غیرقطعی تورینگ قابلحل شدن هستند. کلاس پیچیدگی P یکی از اعضای NP است
نکته : تشخیص P=NP هنوز اثبات نشده است ...
کلاس NP-Complete = مسایلی که برای آنها هیچ الگوریتم شناخته شده قابل اجرا در زمان چند جمله ای وجود ندارد .
کلاس NP-Hard = به معنای حل نشدنی درزمان چندجملهای بر حسب اندازهٔ ورودی مساله (زمان معقول)
معروفترین مسائل ان پی-سخت: ۱- مسئله فروشنده دورهگرد ۲- مسئله بزرگترین خوشه (پیدا کردن بزرگترین زیرگراف کامل)
برای آنکه مسئلهای Intractable یا بغرنج باشد باید اثبات کرد که هیچ الگوریتمی با مرتبه چندجملهای برای آن وجود ندارد. ازنظر بغرنج بودن یا نبودن، مسائل علوم کامپیوتر سه دسته هستند:
۱- مسائلی که الگوریتمهایی با پیچیدگی زمانی چندجملهای برای آنها پیداشده است.
۲- مسائلی که اثباتشده است که بغرنج هستند، یعنی الگوریتم چندجملهای برای آن یافت نمیشود.
۳- مسائلی که بغرنج بودن آنها ثابت نشده است ولی از طرف دیگر هیچ الگوریتم چندجملهای هم برای آنها پیدا نشده است.
مثلاً جستوجوی دودویی در آرایه مرتب با مرتبه زمانی [tex]\theta(\lg n)[/tex] ، مسئله مرتبسازی آرایهها با مرتبه زمانی [tex]\theta(nlgn)[/tex] ، ضرب زنجیرهای ماتریسها با مرتبه زمانی [tex]\theta(n^3)[/tex] از دسته اول هستند. همچنین مسائل کوتاهترین مسیر فلوید با مرتبه زمانی [tex]\theta(n^3)[/tex]، درخت دودویی بهینه [tex]\theta(n^3)[/tex] و مسئله درخت پوشای کمینه پریم [tex]\theta(n^2)[/tex]بااینکه الگوریتمهای نمایی نیز دارند ولی چون برای آنها الگوریتمهایی از نوع چندجملهای یافت شده است از این دستهاند.
تعداد مسائلی که جزو دسته دوم بوده و بغرنج بودن آنها اثباتشده است، نسبتاً کم بوده است. نمونهای از این مسائل دسته دوم، حساب پرزبرگر است.
مسئله کولهپشتی صفر و یک و مسئله فروشنده دورهگرد از دسته سوم هستند.
البته دقت شود در این سوال الگوریتمی پویا وجود دارد که از مرتبه [tex]O(NM)[/tex] است ولی این چند جمله ای بر حسب تعداد اشیا نیست این مساله در هر دو حالت ( حالت اول این که از هر شی یک نمونه باشد و حالت دوم از هر نمونه تعداد بی شمار باشد ) از نوع ان پی کامل است در نتیجه ان پی سخت
۰
۰
ارسال: #۴
RE: Np hard فناوری اطلاعات ۹۵
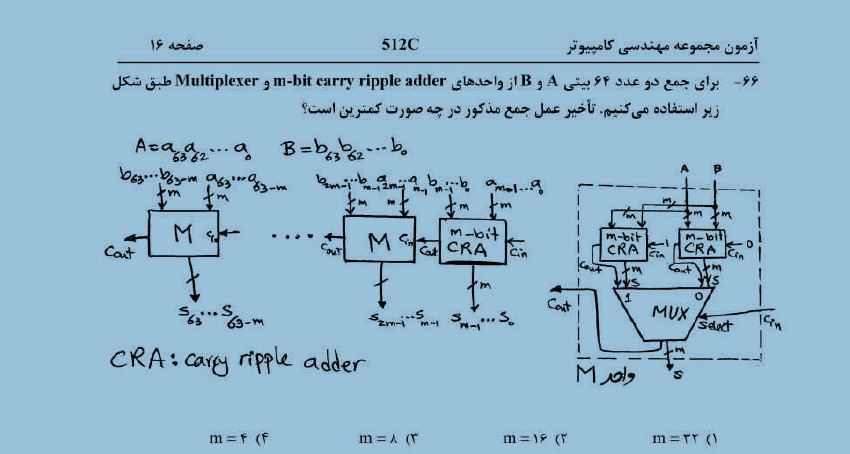 سلام.کسی مبتونه اینو توضیح بده که چجوری جوابش ۸ در میاد .طبق چه تحلیل و فرمولی؟؟؟؟؟؟؟
سلام.کسی مبتونه اینو توضیح بده که چجوری جوابش ۸ در میاد .طبق چه تحلیل و فرمولی؟؟؟؟؟؟؟




ارسال: #۵
RE: Np hard فناوری اطلاعات ۹۵
Can I see some ID?
Feeling left out?
نگران نباش، فقط روی این لینک برای ثبت نام کلیک کن. رمزت رو فراموش کردی؟ اینجا به یادت میاریم! close



