(۲۵ بهمن ۱۳۹۵ ۱۲:۰۵ ب.ظ)wskf نوشته شده توسط:  سلام
جستجوی موفق و ناموفق رو چجوری حساب کرده :؟
کتاب پوران چرا اصلا توضیح نم یده . اه ه ه ه

روشش رو من از اینجا الان یاد گرفتم!

مهمان عزیز شما قادر به مشاهده پیوندهای انجمن مانشت نمی‌باشید. جهت مشاهده پیوندها ثبت نام کنید.


اول باید این عناصر درج بشن. A و B و C سر جای خودشون درج میشن. بعد D هم میخواد در ۳ درج بشه که قبلا A اونجا درج شده، پس میگرده دنبال اولین خونه‌ی خالی که ۶ باشه درج میشه. در آخر هم E میخواد در ۱ درج بشه و خالی هست پس درج میشه
نکته: دقت شود که اگه مثلا E میخواست در ۶ درج بشه، قبلاً D جاش رو گرفته (با اینکه قرار نبوده D اینجا باشه ولی خب در ۳ براش جا نبوده و اولین جای خالی شده اینجا)، حق نداشتیم E رو جای D بذاریم و این بار E هم باید دنبال اولین جای خالی برای خودش می‌بود (میشد ۷).
جدول به صورت زیر میشه:




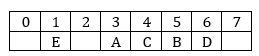
حالا فرض کنیم قرار هست دنبال عنصری مثل Z بگردیم (که در جدول نیست). مثلاً تابع hash گفت که Z باید در ۳ باشه. به ۳ که نگاه کنیم میبینیم A هست و Z نیست. ولی نمیتونیم بگیم جستجو ناموفق بود چون که در بالا به هنگام درج کردن دیدیم که مثلا ممکن بوده Z رو در خانه‌ی ۳ میخواستیم درج کنیم ولی چون قبلا A درج شده، اومدیم و در اولین خانه‌ی خالی درجش کردیم. پس مجبور هستیم برای اینکه مطمئن بشیم که در جدول نیست، تا اولین خانه‌ی خالی رو بگردیم. مثل همون D. برای D اول به ۳ نگاه میکنیم (چون قرار بود در ۳ باشه) ولی چون A هم قبلش قرار بوده در ۳ درج بشه، اومدیم در ۶ (اولین جای خالی) درجش کردیم و برای همین هست که باید تا اولین خالی ادامه بدیم.
از اونجایی که تابع hash ممکن هست به ازای ورودی‌ای مثل Z هر یک از اعداد ۰ تا ۷ رو بده، ما باید تمامی حالت‌ها رو در نظر بگیریم و میانگین بگیریم.
اگه تابع hash خونه‌ی ۳ رو نشون بده، مجبوریم به ۳ و ۴ و ۵ و ۶ و ۷ نگاه کنیم. یعنی اول با ۳ مقایسه میکنیم و میبینیم که Z نیست، بعد تا ۶ هم مقایسه میکنیم. با خود ۷ که خالی هست هم باید مقایسه کنیم چون بدون مقایسه که نمیتونیم متوجه بشیم خالی هست.
اگه تابع hash خونه‌ی خالی رو نشون بده دیگه همون یک مقایسه کافی هست (که میبینیم خونه خالی هست و ادامه نمیدیم).
پس اگه تابع سلول ۰ رو نشون بده، ۱ مقایسه لازم هست چون سلول ۰ خالی هست.
برای سلول ۱، دو مقایسه لازم هست، یکی با خودش (که E رو داره) یکی هم با بعدی
و ...
پس جواب میشه: [tex]\frac{1+2+1+5+4+3+2+1}{8}=\frac{19}{8}[/tex]

برای جستجوی موفق هم هر کدوم از A, B, C, E با اولین جستجو پیدا میشن چون تابع hash مثلا میگه که E توو ۱ هست و مراجعه میکنیم میبنیم اونجا هست. اما برای D تابع میگه که توو ۳ هست ولی میبینیم اونجا A هست. پس هی به راست ادامه میدیم تا پیداش کنیم که میشه ۴ مقایسه.
پس در حالت موفق میشه: [tex]\frac{1+1+1+4+1}{5}=\frac{8}{5}[/tex]