۱
subtitle
ارسال: #۱
رابطه و ترکیب کنکور ۹۰
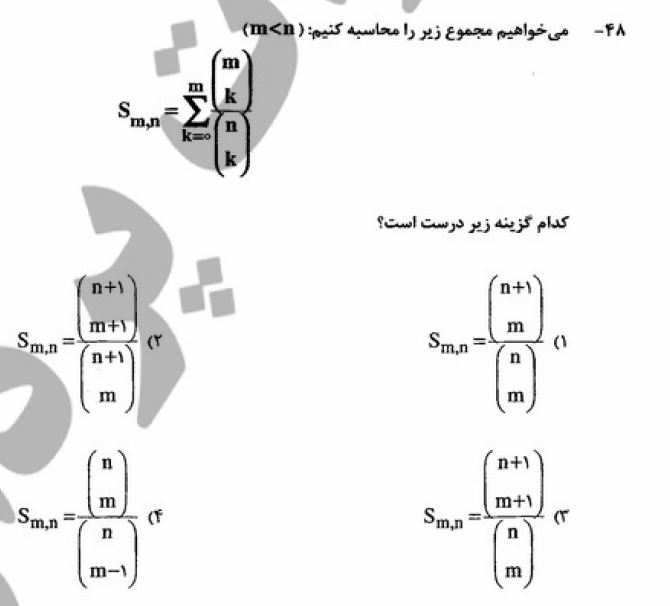
سلام و خسته نباشید ، دوستان من با اطلاعات خودم این سوالو حل کردم و به گزینه اول رسیدم اما جواب سازمان سنجش گزینه ۴ است ، اگه لطف کنید ممنون میشم .

۴
ارسال: #۲
RE: رابطه و ترکیب کنکور ۹۰
سلام. وقت بخیر.
[tex]S_{m,n}=\sum_{k=0}^m\frac{\binom{m}{k}}{\binom{n}{k}}=\sum_{k=0}^m\frac{\frac{m!}{(m-k)!k!}}{\frac{n!}{(n-k)!k!}}[/tex]
[tex]=\sum_{k=0}^m\frac{\frac{(n-k)!}{(m-k)!k!}}{\frac{n!}{m!k!}}=\sum_{k=0}^m\frac{\frac{(n-k)!}{(m-k)!(n-m)!}}{\frac{n!}{m!(n-m)!}}=\sum_{k=0}^m\frac{\binom{n-k}{n-m}}{\binom{n}{m}}=\frac{\binom{n+1}{m}}{\binom{n}{m}}[/tex]
[tex]S_{m,n}=\sum_{k=0}^m\frac{\binom{m}{k}}{\binom{n}{k}}=\sum_{k=0}^m\frac{\frac{m!}{(m-k)!k!}}{\frac{n!}{(n-k)!k!}}[/tex]
[tex]=\sum_{k=0}^m\frac{\frac{(n-k)!}{(m-k)!k!}}{\frac{n!}{m!k!}}=\sum_{k=0}^m\frac{\frac{(n-k)!}{(m-k)!(n-m)!}}{\frac{n!}{m!(n-m)!}}=\sum_{k=0}^m\frac{\binom{n-k}{n-m}}{\binom{n}{m}}=\frac{\binom{n+1}{m}}{\binom{n}{m}}[/tex]
۲
ارسال: #۳
RE: رابطه و ترکیب کنکور ۹۰
سلام. جواب صحیح گزینه ی ۱ هست.
راه حل ساده تر عددگذاری هست.
اثباتش وقت گیر هست.
عددگذاری:
m=2, n=3
[tex]S_{m,n}=\sum^1_{k=0}\frac{C_{k,1}}{Ck,3}=\frac{C0,1}{C0,3}+\frac{C_{1,1}}{C1,3}=\frac{1}{1}+\frac{1}{3}=\frac{4}{3}[/tex]
که فقط گزینه ی ۱ معادلش میشه.
روش اثبات هم تایپش خیلی سخت و وقت گیر هست.
راه حل ساده تر عددگذاری هست.
اثباتش وقت گیر هست.
عددگذاری:
m=2, n=3
[tex]S_{m,n}=\sum^1_{k=0}\frac{C_{k,1}}{Ck,3}=\frac{C0,1}{C0,3}+\frac{C_{1,1}}{C1,3}=\frac{1}{1}+\frac{1}{3}=\frac{4}{3}[/tex]
که فقط گزینه ی ۱ معادلش میشه.
روش اثبات هم تایپش خیلی سخت و وقت گیر هست.
۰
Can I see some ID?
Feeling left out?
نگران نباش، فقط روی این لینک برای ثبت نام کلیک کن. رمزت رو فراموش کردی؟ اینجا به یادت میاریم! close


