۰
subtitle
ارسال: #۱
درخواست راهنمائی در مورد پیچیدگی زمانی
سلام عرض شد.
حالتون خوبه؟
امکانش هست توضیح بفرمائید پیچیدگی زمانی این سوال چی میشه؟
خیلی ممنون.
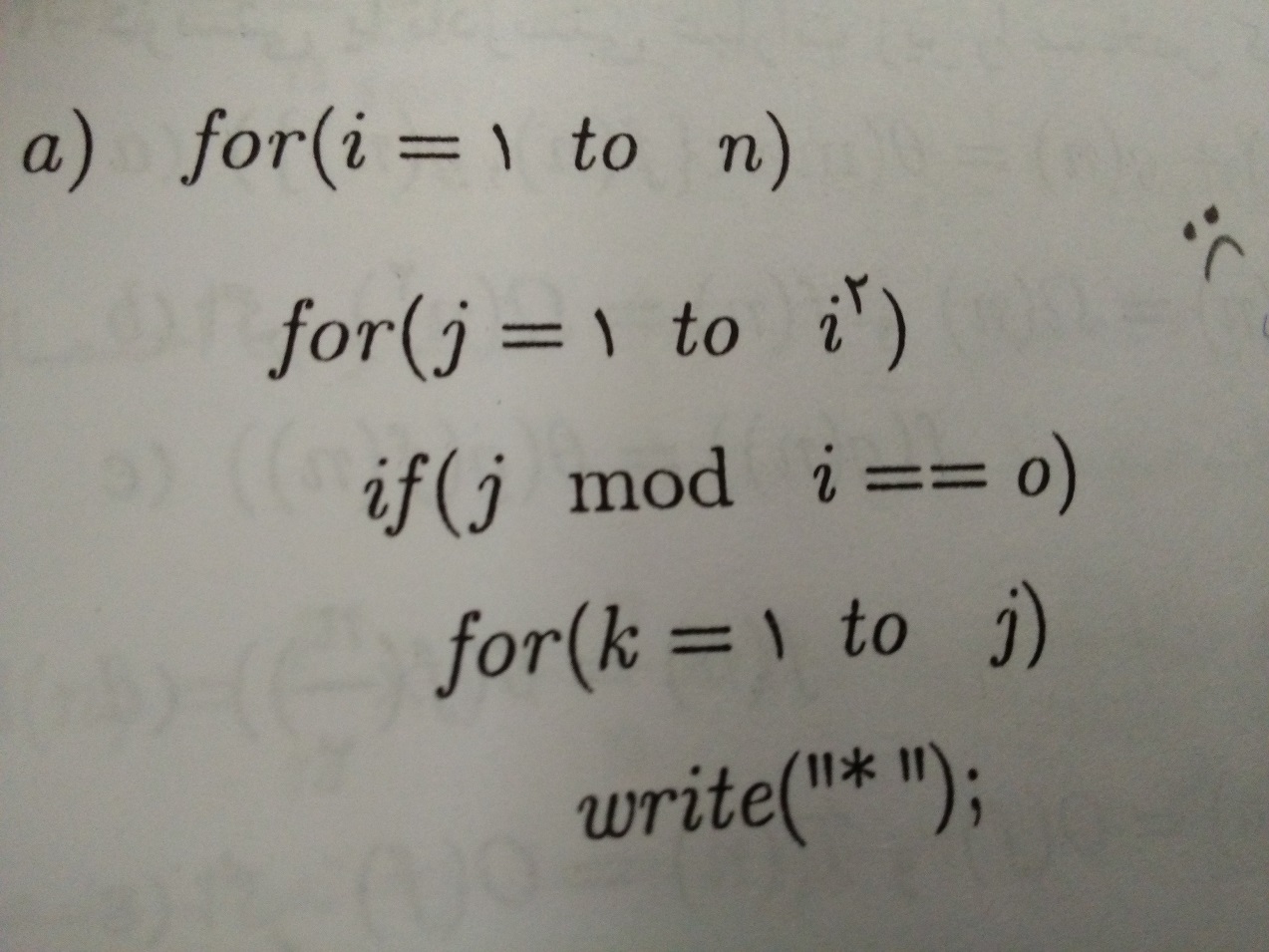
حالتون خوبه؟
امکانش هست توضیح بفرمائید پیچیدگی زمانی این سوال چی میشه؟
خیلی ممنون.
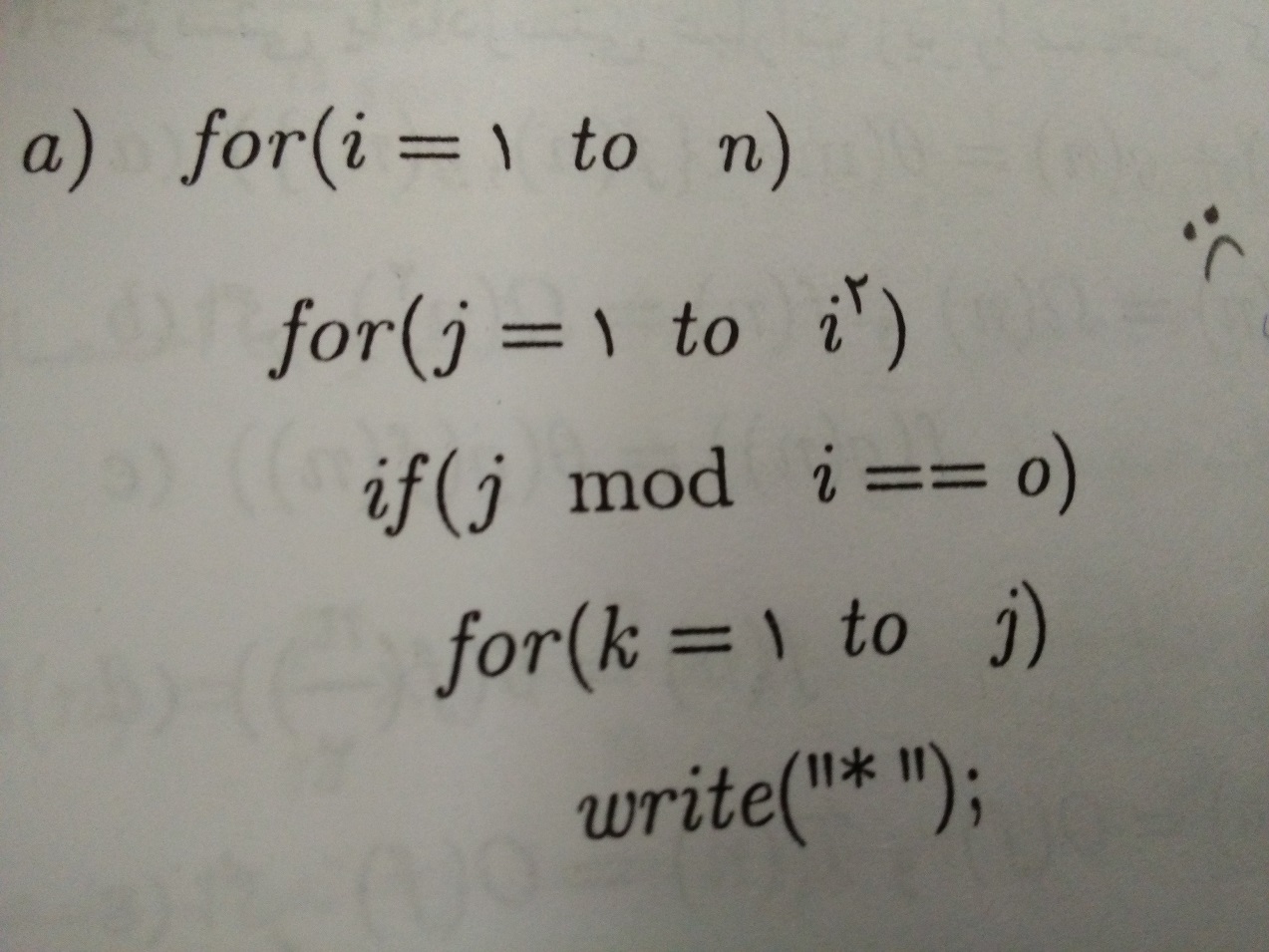
۶
ارسال: #۲
RE: درخواست راهنمائی در مورد پیچیدگی زمانی
جواب نهایی اینه :
[tex]\frac{3n^4 10n^3 9n^2 2n}{24}\mapsto\: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \theta(n^4)[/tex]
البته تو عکس پیوست شده توضیحاتشو نوشتم.
مهمان عزیز شما قادر به مشاهده پیوندهای انجمن مانشت نمیباشید. جهت مشاهده پیوندها ثبت نام کنید.
[tex]\frac{3n^4 10n^3 9n^2 2n}{24}\mapsto\: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \theta(n^4)[/tex]
البته تو عکس پیوست شده توضیحاتشو نوشتم.
مهمان عزیز شما قادر به مشاهده پیوندهای انجمن مانشت نمیباشید. جهت مشاهده پیوندها ثبت نام کنید.
۰
۰
ارسال: #۴
RE: درخواست راهنمائی در مورد پیچیدگی زمانی
توضیح بیشتر برای این سوال:
فرض کنید که n=1 باشد پس i=1 شده و j=1 و شرط if درست است و دستور سطر چهارم ۱ بار اجرا میشود. پس یک * چاپ میشود.
فرض کنید که n=2 باشد پس برای بار اول اجرای حلقه بیرونی i=1 میشود, این فاز مثل سطر بالا اجرا میشود و یک * چاپ میشود. حالا در اجرای دوم حلقه بیرونی i=2 میشود.حالا حلقه سطر دوم برای j=1 to 4 اجرا میشود و سپس سراغ بررسی شرط if میرود.
این شرط برای J=2 , 4 درست است زیرا ۲%۴=۰ و ۲%۲=۰ . برای هر کدومشون هم J بار ستاره چاپ میشه یعنی ** و **** در خروجی چاپ میشه. در کل برای n=2 , ستاره * ۷ بار چاپ شد.
از روی جزییات بالا میشه تعداد چاپ * رو رو برای n های بزرگتر پیدا کرد.
فرض کنید که n=1 باشد پس i=1 شده و j=1 و شرط if درست است و دستور سطر چهارم ۱ بار اجرا میشود. پس یک * چاپ میشود.
فرض کنید که n=2 باشد پس برای بار اول اجرای حلقه بیرونی i=1 میشود, این فاز مثل سطر بالا اجرا میشود و یک * چاپ میشود. حالا در اجرای دوم حلقه بیرونی i=2 میشود.حالا حلقه سطر دوم برای j=1 to 4 اجرا میشود و سپس سراغ بررسی شرط if میرود.
این شرط برای J=2 , 4 درست است زیرا ۲%۴=۰ و ۲%۲=۰ . برای هر کدومشون هم J بار ستاره چاپ میشه یعنی ** و **** در خروجی چاپ میشه. در کل برای n=2 , ستاره * ۷ بار چاپ شد.
از روی جزییات بالا میشه تعداد چاپ * رو رو برای n های بزرگتر پیدا کرد.
۰
ارسال: #۵
RE: درخواست راهنمائی در مورد پیچیدگی زمانی
میشه روش حل این سوال رو با سیگما هم توضیح بدین؟
ارسال: #۶
RE: درخواست راهنمائی در مورد پیچیدگی زمانی
(۰۸ آبان ۱۳۹۵ ۱۲:۰۱ ب.ظ)Flora نوشته شده توسط: میشه روش حل این سوال رو با سیگما هم توضیح بدین؟سلام. لزوماََ همیشه خوب نیست از سیگما استفاده بشه برای حل سوال. حتی شاید جواب غلط بده! چون اون تعدادی که فرض و گرد کردیم اجرا نشه.
یه نمونه ش اینجاست که سیگما به ما کران بالا رو میده، مرتبه ش یعنی orderش درست هست. اما ضرایبش نه، چون کران بالا در نظر گرفتیم. یعنی اگه بخوایم سیگما بنویسیم، میشه:
[tex]\sum^n_{i=1}\sum^{i^2}_{j=1}\sum^j_{k=1}[/tex] در حالی که سیگمای داخلی (داخلی ترین حلقه ی for) برای تمامی k ها از ۱ تا n اجرا نمیشه و فقط به ازای j mod i ==0 اجرا میشه.
[tex]\sum^n_{i=1}\sum^{i^2}_{j=1}\sum^j_{k=1}1=\: \sum^n_{i=1}\sum^{i^2}_{j=1}j=\sum^n_{i=1}(1+4+9+...+i^2)=\sum^n_{i=1}\frac{i(i+1)(2i+1)}{6}=\frac{1}{6}\sum^n_{i=1}2i^3+3i^2+i=\frac{2}{6}\sum i^3+\frac{3}{6}\sum i^2+\frac{1}{6}\sum i=\frac{\: 1}{3}(\frac{n(n+1)}{2})^2+\frac{1}{2}(\frac{n(n+1)(2n+1)}{6})+\frac{\frac{1}{6}.n(n+1)}{2}=\theta(n^4)\: \: \longrightarrow\: T(n)\in O(n^4)[/tex]
Can I see some ID?
Feeling left out?
نگران نباش، فقط روی این لینک برای ثبت نام کلیک کن. رمزت رو فراموش کردی؟ اینجا به یادت میاریم! close


