۰
subtitle
ارسال: #۱
مرتبه رابطه بازگشتی
کدام گزینه بهترین پاسخ برای رابطه زیر است؟
[tex]T(n)=T(n/4) T(3n/4) n^{2}[/tex]
در صورتی که [tex]T(1)=1[/tex]
الف) [tex]\theta (nlogn)[/tex]
ب) [tex]\theta (n^{2}logn)[/tex]
ج) [tex]\theta (n^{3})[/tex]
د) [tex]\theta (n^{2})[/tex]
[tex]T(n)=T(n/4) T(3n/4) n^{2}[/tex]
در صورتی که [tex]T(1)=1[/tex]
الف) [tex]\theta (nlogn)[/tex]
ب) [tex]\theta (n^{2}logn)[/tex]
ج) [tex]\theta (n^{3})[/tex]
د) [tex]\theta (n^{2})[/tex]
۱
ارسال: #۲
RE: مرتبه رابطه بازگشتی
اگه شما درخت این رابطه رو بکشید یه درخت نا متوازن داره که به یکی با ارتفاع [tex]log_{4}(n)[/tex] و دیگری [tex]log_{\frac{4}{3}}(n)[/tex]
که اگه شما یه مجموع بزنی حد بالا و پایین بدست میاد و در نهایت میشه [tex]\Theta( n^{2})[/tex]
این یکی از سری ها میشه:
[tex]T(n) < n^{2}\sum _{i = 0}^{log_{\frac {4}{3}}n}(\frac{10}{16})^{i}< cn^{2} = O(n^{2})[/tex]
واسه حد پایین هم سری تا [tex]log_{4}n[/tex] بگیرید و در نهایت میشه
[tex]\Theta( n^{2})[/tex]
که اگه شما یه مجموع بزنی حد بالا و پایین بدست میاد و در نهایت میشه [tex]\Theta( n^{2})[/tex]
این یکی از سری ها میشه:
[tex]T(n) < n^{2}\sum _{i = 0}^{log_{\frac {4}{3}}n}(\frac{10}{16})^{i}< cn^{2} = O(n^{2})[/tex]
واسه حد پایین هم سری تا [tex]log_{4}n[/tex] بگیرید و در نهایت میشه
[tex]\Theta( n^{2})[/tex]
۲
ارسال: #۳
RE: مرتبه رابطه بازگشتی
با سلام
جواب این رابطه بازگشتی [tex]n^{2}\log n[/tex] میشه
توی کتاب طراحی الگوریتم آقای مقسمی هم تفریبا چنین مثالی هست.
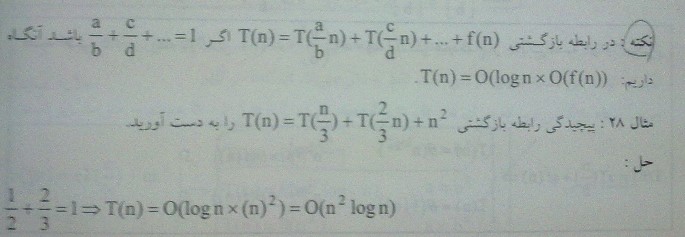
طبق نکته کتاب آقای مقسمی :
[tex]\frac{3}{4} \frac{1}{4}=1 \Rightarrow n^{2}\log n[/tex]
جواب این رابطه بازگشتی [tex]n^{2}\log n[/tex] میشه
توی کتاب طراحی الگوریتم آقای مقسمی هم تفریبا چنین مثالی هست.
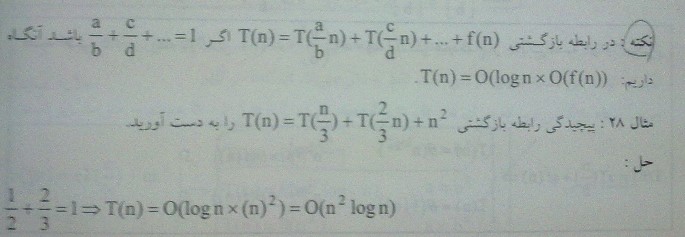
طبق نکته کتاب آقای مقسمی :
[tex]\frac{3}{4} \frac{1}{4}=1 \Rightarrow n^{2}\log n[/tex]
۱
ارسال: #۴
RE: مرتبه رابطه بازگشتی
یه روش سریع تر هم هست که در آن :
[tex]T(3n/4) T(n/4)= O(n)[/tex]
و طبق قضیه اصلی جواب گزینه ۴ میشه.
[tex]T(3n/4) T(n/4)= O(n)[/tex]
و طبق قضیه اصلی جواب گزینه ۴ میشه.
ارسال: #۵
RE: مرتبه رابطه بازگشتی
ارسال: #۶
RE: مرتبه رابطه بازگشتی
(۱۱ شهریور ۱۳۹۲ ۰۱:۲۷ ق.ظ)SnowBlind نوشته شده توسط:(10 شهریور ۱۳۹۲ ۱۲:۳۵ ب.ظ)Masoud05 نوشته شده توسط: یه روش سریع تر هم هست که در آن :
[tex]T(3n/4) T(n/4)= O(n)[/tex]
و طبق قضیه اصلی جواب گزینه ۴ میشه.
قضیه اصلی مگه واسه رابطه های به فرم [tex]aT(n/b) f(n)[/tex] نیست
ممنون از توجه تون . دقیقا به همین علت که گفتید ، من در ۲ مرحله جواب گرفتم . مرحله اولش از یه نکته تستی که در کتاب های کنکور اومده استفاده کردم ( که البته روش علمی نیست بنظرم اما برا تست جواب میده ) و مرحله دوم قضیه مستر زدم . این روشی که من گفتم یه خورده خیلی سریع هست و امکان اشتباه هم هست اگه باهاش کار نکرده باشید. بنظرم ساده ترین کار درخت کشیدن باشه .
۱
ارسال: #۷
RE: مرتبه رابطه بازگشتی
جواب این دوست عزیز که آخر جواب داده درست هستش
اگر مجموع برابر با ۱ بشه جواب میشه
log n * f
اینجا میشه n^{2}logn
اگر مجموع برابر با ۱ بشه جواب میشه
log n * f
اینجا میشه n^{2}logn
۰
ارسال: #۸
RE: مرتبه رابطه بازگشتی
سلام
در کتاب ۶۰۰ مسئله ی دکتر قدسی دقیقا" مشابه همین سوال هستش که جواب داده شده :
[tex]n^{2}logn[/tex]
یعنی گزینه ۲ , ولی در پاسخنامه گزینه ۴ رو علامت زدن
از روش تستی هم بخوایم بریم گزینه ۲ میشه
آخرش کدوم جوابه ؟؟
در کتاب ۶۰۰ مسئله ی دکتر قدسی دقیقا" مشابه همین سوال هستش که جواب داده شده :
[tex]n^{2}logn[/tex]
یعنی گزینه ۲ , ولی در پاسخنامه گزینه ۴ رو علامت زدن

از روش تستی هم بخوایم بریم گزینه ۲ میشه
آخرش کدوم جوابه ؟؟
۰
ارسال: #۹
RE: مرتبه رابطه بازگشتی
سلام دوستان
به نظر من اگه طبق مستر بریم میشه گزینه ۴/
حالا کسی میدونه جواب درستش واقعا چیه؟؟؟
به نظر من اگه طبق مستر بریم میشه گزینه ۴/
حالا کسی میدونه جواب درستش واقعا چیه؟؟؟
۰
ارسال: #۱۰
RE: مرتبه رابطه بازگشتی
با سلام
در کتاب آقای قدسی عین این مسئله اومده. در گزینه ها جواب زده شده [tex]n^{2}[/tex] ولی در راه حل ها که مسئله حل شده در نهایت پاسخ درست [tex]n^{2}logn[/tex] اعلام شده .
جواب کتاب آقای قدسی :
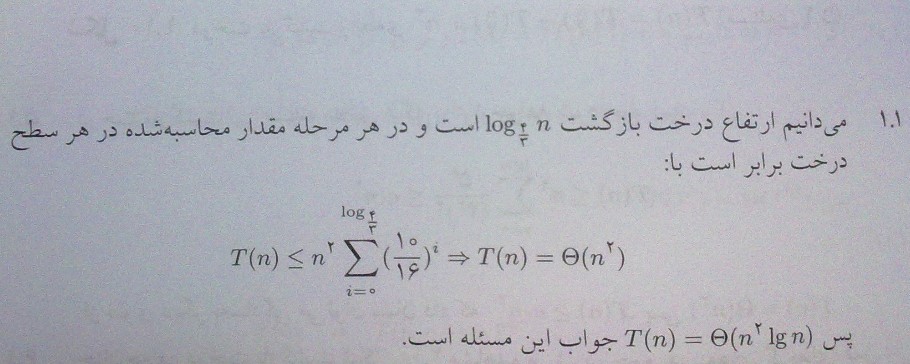
در کتاب آقای قدسی عین این مسئله اومده. در گزینه ها جواب زده شده [tex]n^{2}[/tex] ولی در راه حل ها که مسئله حل شده در نهایت پاسخ درست [tex]n^{2}logn[/tex] اعلام شده .
جواب کتاب آقای قدسی :
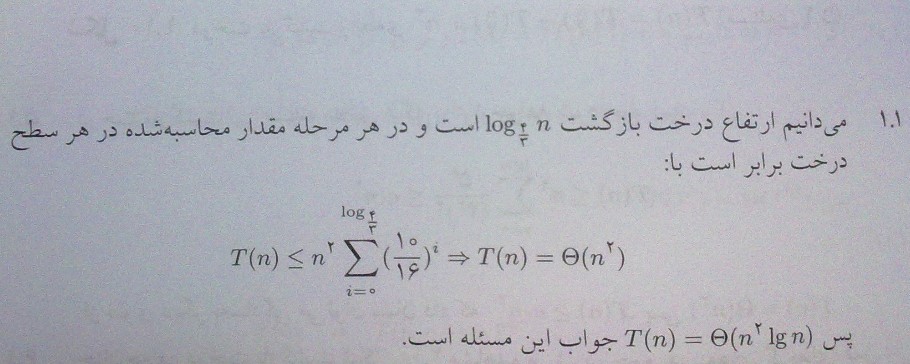
۰
ارسال: #۱۱
RE: مرتبه رابطه بازگشتی
دوستان عزیز طبق قرمول : در صورتی که در رابطه ( T(n) = T(a/b) + T(c/d) + F(n
a/b +c/d برابر با یک باشد جواب میشود ( O(log n ) * F(n
پس اینجا هم چون برابر یک میشه پس جواب میشه n^2 log n
a/b +c/d برابر با یک باشد جواب میشود ( O(log n ) * F(n
پس اینجا هم چون برابر یک میشه پس جواب میشه n^2 log n
موضوعهای مرتبط با این موضوع... |
|||||
| موضوع: | نویسنده | پاسخ: | بازدید: | آخرین ارسال | |
| سلام لطفاً یکی به من بگه مرتبه زمانی ها چطوری به log تبدیل میشن فرمول داره؟؟ | Azadam | ۶ | ۷,۵۷۱ |
۰۶ دى ۱۴۰۰ ۰۹:۰۲ ق.ظ آخرین ارسال: Soldier's life |
|
| نظر در رابطه با استاد داور | علیصا | ۰ | ۲,۶۴۱ |
۱۴ مهر ۱۴۰۰ ۰۶:۰۵ ب.ظ آخرین ارسال: علیصا |
|
| مرتبه ایجاد درخت | rad.bahar | ۱ | ۴,۳۴۱ |
۳۰ مهر ۱۳۹۹ ۰۳:۳۴ ب.ظ آخرین ارسال: rad.bahar |
|
| مرتبه شبه کد | rad.bahar | ۱ | ۳,۱۳۱ |
۲۲ مهر ۱۳۹۹ ۰۹:۳۲ ب.ظ آخرین ارسال: BBumir |
|
| حل مساله مرتبه زمانی حلقه های تو در تو | sarashahi | ۱۶ | ۲۷,۷۲۶ |
۱۹ خرداد ۱۳۹۹ ۰۱:۱۶ ب.ظ آخرین ارسال: gillda |
|
| مرتبه زمانی | Sanazzz | ۱۷ | ۲۶,۹۸۱ |
۰۹ اردیبهشت ۱۳۹۹ ۰۶:۴۶ ب.ظ آخرین ارسال: mohsentafresh |
|
| مرتبه زمانی یافتن قطر | Sepideh96 | ۲ | ۴,۸۷۲ |
۰۸ آذر ۱۳۹۸ ۰۴:۳۴ ب.ظ آخرین ارسال: erfan30 |
|
| مرتبه مانی | Sanazzz | ۳ | ۵,۰۰۷ |
۰۵ خرداد ۱۳۹۸ ۰۲:۳۶ ب.ظ آخرین ارسال: Sanazzz |
|
| مرتبه زمانی | Sanazzz | ۰ | ۲,۵۷۶ |
۰۴ بهمن ۱۳۹۷ ۰۵:۴۱ ب.ظ آخرین ارسال: Sanazzz |
|
| درخواست(محاسبه پیچیدگی زمانی)(بخش روابط بازگشتی) | Saman | ۶ | ۹,۲۸۷ |
۲۷ خرداد ۱۳۹۷ ۰۳:۲۴ ب.ظ آخرین ارسال: saeed_vahidi |
|
Can I see some ID?
Feeling left out?
نگران نباش، فقط روی این لینک برای ثبت نام کلیک کن. رمزت رو فراموش کردی؟ اینجا به یادت میاریم! close



