۰
subtitle
ارسال: #۱
سری دوم سوالات
سری دوم و سری آخر سوالات آنالیز ترکیبی برای تکمیل این بخش در امار و احتمال است. چون بعضی مسائل و تکنیکهای خاص شمارش در گسسته است، با این سری مسائل مبحث اول را آمار و احتمال به پایان می بریم. بنابراین بحث شمارش در گسسته هم انجام خواهد شد.
۱-بچند طریق ۱۰ نفر میتوانند برای بازی والیبال به دو گروه مساوی تقسیم شوند؟
الف- ۱۲۶ ب- ۱۶۸ ج- ۲۵۲ د- ۵۰۴
۲- ده نقطه مانند A,B,…..در یک صفحه انتخاب میکنیم بطوریکه هیچ سه نقطه ای در امتداد یکدیگر قرار نگیرند بوسیله این نقاط چند مثلث میتوان تشکیل داد؟
الف- ۱۲۰ ب- ۶۰ ج- ۱۸۰ د-۳۰
۳- با ارقام ۱،۲،۳،۴،۵ چند عدد چهار رقمی میتوان نوشت که بر چهار بخش پذیر باشند(تکرار ارقام مجاز است)؟
الف- ۱۲۵ ب- ۲۱۵ ج- ۲۵۱ د- ۵۱۲
۴- بچند طریق مختلف میتوان ۴ اسکی باز را با سه نقاله بظرفیتهای بترتیب ۲،۱ و ۳ نفره میتوان به بالای کوهی برد؟
الف- ۴ ب-۶ ج- ۳۸ د-۱۲
۵-ظرفی حاوی nتوپ سفید و nتوپ سیاه است. تعداد حالاتی که میتوان از این ظرف n توپ انتخاب کرد برابر است با:
(جواب را بدست آورید.)
۱-بچند طریق ۱۰ نفر میتوانند برای بازی والیبال به دو گروه مساوی تقسیم شوند؟
الف- ۱۲۶ ب- ۱۶۸ ج- ۲۵۲ د- ۵۰۴
۲- ده نقطه مانند A,B,…..در یک صفحه انتخاب میکنیم بطوریکه هیچ سه نقطه ای در امتداد یکدیگر قرار نگیرند بوسیله این نقاط چند مثلث میتوان تشکیل داد؟
الف- ۱۲۰ ب- ۶۰ ج- ۱۸۰ د-۳۰
۳- با ارقام ۱،۲،۳،۴،۵ چند عدد چهار رقمی میتوان نوشت که بر چهار بخش پذیر باشند(تکرار ارقام مجاز است)؟
الف- ۱۲۵ ب- ۲۱۵ ج- ۲۵۱ د- ۵۱۲
۴- بچند طریق مختلف میتوان ۴ اسکی باز را با سه نقاله بظرفیتهای بترتیب ۲،۱ و ۳ نفره میتوان به بالای کوهی برد؟
الف- ۴ ب-۶ ج- ۳۸ د-۱۲
۵-ظرفی حاوی nتوپ سفید و nتوپ سیاه است. تعداد حالاتی که میتوان از این ظرف n توپ انتخاب کرد برابر است با:
(جواب را بدست آورید.)
۰
ارسال: #۲
سری دوم سوالات
سوال اول
گزینه ۴
ابتدا ترکیب ۵ نفر از ۱۰ نفر رو انتخاب می کنیم و از اونجا که دو تیم هستن در یک جایگشت !۲ هم ضرب میشن
سوال چهارم
در کل ۶ تا ظرفیت برای اسکی بازها داریم و ۴ اسکی باز که می خوان سوار این نقالهها بشن. فک کنم اینطوری بشه
۱۵=(C(6,4
سوال پنجم
ظاهرا رنگ توپها نقشی در حل نداره. خب ۲n تا توپ داریم بخوایم n تا شو برداریم میشه:
(C(2n,n
برای این سوال یه راه حل دیگه هم به ذهنم میرسه. نمیدونم کدومش درسته.
۲n * 2n-1 * 2n-2 * 2n -3 * .... * n
استدلالم اینه که اول ۲n تا انتخاب داریم. یک توپ برمیداریم. تعداد توپ های باقیمانده میشه ۲n-1 و ... تا زمانیکه تعداد توپ هایی که برداشتیم به n توپ برسه ادامه میدیم.
گزینه ۴
ابتدا ترکیب ۵ نفر از ۱۰ نفر رو انتخاب می کنیم و از اونجا که دو تیم هستن در یک جایگشت !۲ هم ضرب میشن
سوال چهارم
در کل ۶ تا ظرفیت برای اسکی بازها داریم و ۴ اسکی باز که می خوان سوار این نقالهها بشن. فک کنم اینطوری بشه
۱۵=(C(6,4
سوال پنجم
ظاهرا رنگ توپها نقشی در حل نداره. خب ۲n تا توپ داریم بخوایم n تا شو برداریم میشه:
(C(2n,n
برای این سوال یه راه حل دیگه هم به ذهنم میرسه. نمیدونم کدومش درسته.
۲n * 2n-1 * 2n-2 * 2n -3 * .... * n
استدلالم اینه که اول ۲n تا انتخاب داریم. یک توپ برمیداریم. تعداد توپ های باقیمانده میشه ۲n-1 و ... تا زمانیکه تعداد توپ هایی که برداشتیم به n توپ برسه ادامه میدیم.
۰
ارسال: #۳
RE: سری دوم سوالات
سوال اول: گزینه ۱
[tex]\frac{\binom{10}{5}\binom{5}{5}}{2!}[/tex]
به خاطر حالات تکراری در دو گروه تقسیم بر ۲ شد.
مثلاً فرض کنید این ۱۰ نفر هستند:
A, B, C, D, E, F, G, H, J, K
یک گروه از این ۱۰ نفر به این صورت هست:
A, B, C, D, E
و گروه دیگر:
F, G, H, J, K
حالا بین این دو تقسیم بندی تفاوتی نیست:
[tex]\left \{ A, B, C, D, E \right \} \left \{ F, G, H, J, K \right \}[/tex]
و
[tex]\left \{ F, G, H, J, K \right \} \left \{A, B, C, D, E \right \}[/tex]
[tex]\frac{\binom{10}{5}\binom{5}{5}}{2!}[/tex]
به خاطر حالات تکراری در دو گروه تقسیم بر ۲ شد.
مثلاً فرض کنید این ۱۰ نفر هستند:
A, B, C, D, E, F, G, H, J, K
یک گروه از این ۱۰ نفر به این صورت هست:
A, B, C, D, E
و گروه دیگر:
F, G, H, J, K
حالا بین این دو تقسیم بندی تفاوتی نیست:
[tex]\left \{ A, B, C, D, E \right \} \left \{ F, G, H, J, K \right \}[/tex]
و
[tex]\left \{ F, G, H, J, K \right \} \left \{A, B, C, D, E \right \}[/tex]
۰
ارسال: #۴
RE: سری دوم سوالات
سوال چهارم: گزینه ۳
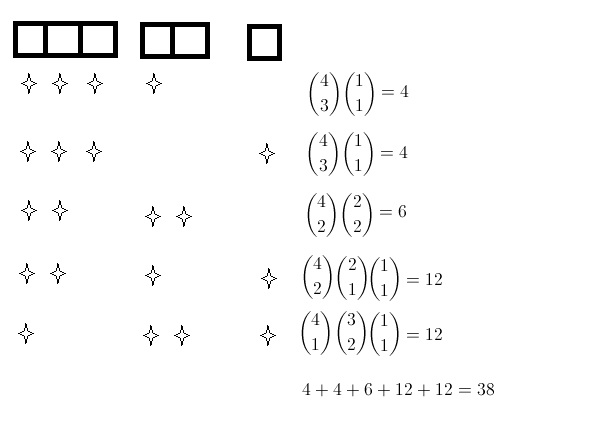
سوال ۵:
تعداد حالات برابر است با:
[tex]\binom{n}{0}\binom{n}{n} \binom{n}{1}\binom{n}{n-1} \binom{n}{2}\binom{n}{n-2} ... \binom{n}{n}\binom{n}{0}[/tex]
می دانیم:
[tex]\binom{n}{r}=\binom{n}{n-r}[/tex]
در نتیجه داریم:
[tex]\binom{n}{0}^{2} \binom{n}{1}^{2} \binom{n}{2}^{2} ... \binom{n}{n}^{2}=\sum_{k=0}^{n}\binom{n}{k}^{2}=\binom{2n}{n}[/tex]
سوال ۳: گزینه ۱
اعدادی که بر ۴ بخش پذیرند دو حالت دارند:
۱) دهگانشان اعداد ۱ ،۳ یا ۵ است که در این صورت رقم یکان باید ۲ باشد
۲) دهگانشان اعداد ۲ یا ۴ است و رقم یکانشان باید عدد ۴ باشد.
بقیه ارقام هر کدام از این ۵ عدد می توانند باشند و چون ارقام تکراری مجاز است داریم:
حالت ۱:
[tex]5\times 5\times 3\times 1=75[/tex]
حالت ۲:
[tex]5\times 5\times 2\times 1=25[/tex]
در نتیجه کل حالات برابر است با:
[tex]75 25=125[/tex]
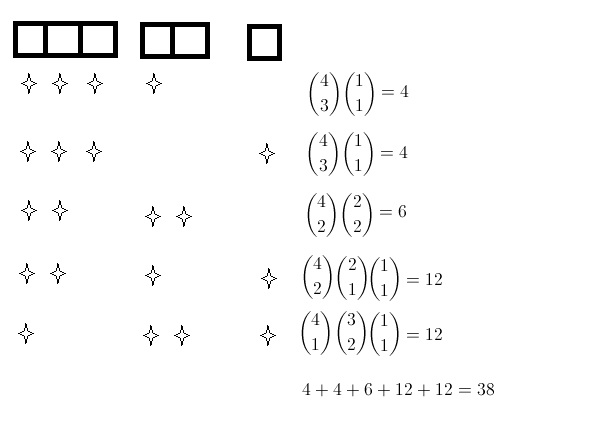
سوال ۵:
تعداد حالات برابر است با:
[tex]\binom{n}{0}\binom{n}{n} \binom{n}{1}\binom{n}{n-1} \binom{n}{2}\binom{n}{n-2} ... \binom{n}{n}\binom{n}{0}[/tex]
می دانیم:
[tex]\binom{n}{r}=\binom{n}{n-r}[/tex]
در نتیجه داریم:
[tex]\binom{n}{0}^{2} \binom{n}{1}^{2} \binom{n}{2}^{2} ... \binom{n}{n}^{2}=\sum_{k=0}^{n}\binom{n}{k}^{2}=\binom{2n}{n}[/tex]
سوال ۳: گزینه ۱
اعدادی که بر ۴ بخش پذیرند دو حالت دارند:
۱) دهگانشان اعداد ۱ ،۳ یا ۵ است که در این صورت رقم یکان باید ۲ باشد
۲) دهگانشان اعداد ۲ یا ۴ است و رقم یکانشان باید عدد ۴ باشد.
بقیه ارقام هر کدام از این ۵ عدد می توانند باشند و چون ارقام تکراری مجاز است داریم:
حالت ۱:
[tex]5\times 5\times 3\times 1=75[/tex]
حالت ۲:
[tex]5\times 5\times 2\times 1=25[/tex]
در نتیجه کل حالات برابر است با:
[tex]75 25=125[/tex]
۰
ارسال: #۵
RE: سری دوم سوالات
۱: الف
۲: الف
۳: الف
۴: ج
سارا جوابها رو خیلی زیبا توضیح داده که ازش خیلی ممنون هستم پس در این لحظه من دیگه زحمت توضیح دادن رو به خودم نمیدم!!!!!!!!!!
فقط یه نکته رو اضافه میکنم که اعدادی بر ۴ بخشپذیرن که دو رقم سمت راست اونها مضربی از چهار باشه( یعنی دورقم آخر سمت راست بر ۴ بخشپذیر باشه) یعنی به بیان دیگه در تست شماره سه دورقم آخر یکی از اعداد ۱۲، ۲۴، ۴۴، ۳۲، ۵۲ میتونه باشه (یعنی پنج حالت مختلف وجود داره) و برای دو رقم سمت چپ هرکدام ۵ حالت وجود داره پس تعداد کل حالات برابر است با: ۱۲۵= ۵*۵*۵
۲: الف
۳: الف
۴: ج
سارا جوابها رو خیلی زیبا توضیح داده که ازش خیلی ممنون هستم پس در این لحظه من دیگه زحمت توضیح دادن رو به خودم نمیدم!!!!!!!!!!
فقط یه نکته رو اضافه میکنم که اعدادی بر ۴ بخشپذیرن که دو رقم سمت راست اونها مضربی از چهار باشه( یعنی دورقم آخر سمت راست بر ۴ بخشپذیر باشه) یعنی به بیان دیگه در تست شماره سه دورقم آخر یکی از اعداد ۱۲، ۲۴، ۴۴، ۳۲، ۵۲ میتونه باشه (یعنی پنج حالت مختلف وجود داره) و برای دو رقم سمت چپ هرکدام ۵ حالت وجود داره پس تعداد کل حالات برابر است با: ۱۲۵= ۵*۵*۵
۰
ارسال: #۶
سری دوم سوالات
فکر میکنم برای سوال اول اگر در سوال مطرح شده بود که ۱۰ نفر را میخواهیم در دو گروه مجزا مثلا اول و دوم تقسیم کنیم جواب !۲*c(10,5 اما اینجا چون دو گروه یکسان هستند نیاز به ضرب در !۲ نیست
سارا خانم من متوجه نشدم چرا جواب را به !۲ تقسیم کردید!
سارا خانم من متوجه نشدم چرا جواب را به !۲ تقسیم کردید!
۰
ارسال: #۷
RE: سری دوم سوالات
سوال ۴ میشه از طریق توزیع n شی متمایز در k سلول حل کرد:
۴نفر که ۳نفر با نقاله ۳ نفره و یک نفر بانقاله ۲نفره + ۴نفر که ۳نفر با نقاله ۳نفره و یک نفر با نقاله یک نفره +۴نفر که ۲نفر با نقاله ۳نفره و ۲نفر با نقاله ۲نفره + ۴نفر که ۲نفر با نقاله ۳نفره و یک نفر با نقاله ۲نفره و یک نفر با نقاله یک نفره + ۴نفر که یک نفر با نقاله ۳نفره و ۲نفر با نقاله ۲نفره و یک نفر با نقاله یک نفره
که میشه:
[tex]\frac{4!}{3!1!} \frac{4!}{3!1!} \frac{4!}{2!1!1!} \frac{4!}{2!2!} \frac{4!}{1!2!1!}[/tex]
که برابر ۳۸ است
۴نفر که ۳نفر با نقاله ۳ نفره و یک نفر بانقاله ۲نفره + ۴نفر که ۳نفر با نقاله ۳نفره و یک نفر با نقاله یک نفره +۴نفر که ۲نفر با نقاله ۳نفره و ۲نفر با نقاله ۲نفره + ۴نفر که ۲نفر با نقاله ۳نفره و یک نفر با نقاله ۲نفره و یک نفر با نقاله یک نفره + ۴نفر که یک نفر با نقاله ۳نفره و ۲نفر با نقاله ۲نفره و یک نفر با نقاله یک نفره
که میشه:
[tex]\frac{4!}{3!1!} \frac{4!}{3!1!} \frac{4!}{2!1!1!} \frac{4!}{2!2!} \frac{4!}{1!2!1!}[/tex]
که برابر ۳۸ است
ارسال: #۸
RE: سری دوم سوالات
(۱۸ مرداد ۱۳۹۰ ۱۰:۰۷ ب.ظ)narges_r نوشته شده توسط: سوال ۴ میشه از طریق توزیع n شی متمایز در k سلول حل کرد:
۴نفر که ۳نفر با نقاله ۳ نفره و یک نفر بانقاله ۲نفره + ۴نفر که ۳نفر با نقاله ۳نفره و یک نفر با نقاله یک نفره +۴نفر که ۲نفر با نقاله ۳نفره و ۲نفر با نقاله ۲نفره + ۴نفر که ۲نفر با نقاله ۳نفره و یک نفر با نقاله ۲نفره و یک نفر با نقاله یک نفره + ۴نفر که یک نفر با نقاله ۳نفره و ۲نفر با نقاله ۲نفره و یک نفر با نقاله یک نفره
که میشه:
[tex]\frac{4!}{3!1!} \frac{4!}{3!1!} \frac{4!}{2!1!1!} \frac{4!}{2!2!} \frac{4!}{1!2!1!}[/tex]
که برابر ۳۸ است
استدلال من کجاش اشتباهه؟
در کل ۶ تا ظرفیت برای اسکی بازها داریم و ۴ اسکی باز که می خوان سوار این نقالهها بشن.
۰
ارسال: #۹
سری دوم سوالات
برای حل سوال دوم هم فکر میکنم باید c(10,3 حساب کرد که برابر ۱۲۰ میشود
اینطوری کلی در نظر گرفتن ظرفیت نقالهها به معنی در نظر نگرفتن شرایط سوال هست و همینطور اینکه مثلا اگر ۲نقاله به ظرفیتهای ۵ و ۱ هم داشتیم بازهم ظرفیت نقالهها ۶ میشد ولی میبینید که این حالت جز شرایط صورت مسئله نیست
(۱۸ مرداد ۱۳۹۰ ۱۰:۳۱ ب.ظ)ehsan_nekooee نوشته شده توسط:درسته که ۶ ظرفیت برای اسکی بازها داریم اما برای این ۶ ظرفیت شرایطی در نظر گرفته شده که در صورت سوال مطرح شده که این شرایط همان ظرفیت نقاله هاست(18 مرداد ۱۳۹۰ ۱۰:۰۷ ب.ظ)narges_r نوشته شده توسط: سوال ۴ میشه از طریق توزیع n شی متمایز در k سلول حل کرد:
۴نفر که ۳نفر با نقاله ۳ نفره و یک نفر بانقاله ۲نفره + ۴نفر که ۳نفر با نقاله ۳نفره و یک نفر با نقاله یک نفره +۴نفر که ۲نفر با نقاله ۳نفره و ۲نفر با نقاله ۲نفره + ۴نفر که ۲نفر با نقاله ۳نفره و یک نفر با نقاله ۲نفره و یک نفر با نقاله یک نفره + ۴نفر که یک نفر با نقاله ۳نفره و ۲نفر با نقاله ۲نفره و یک نفر با نقاله یک نفره
که میشه:
[tex]\frac{4!}{3!1!} \frac{4!}{3!1!} \frac{4!}{2!1!1!} \frac{4!}{2!2!} \frac{4!}{1!2!1!}[/tex]
که برابر ۳۸ است
استدلال من کجاش اشتباهه؟
در کل ۶ تا ظرفیت برای اسکی بازها داریم و ۴ اسکی باز که می خوان سوار این نقالهها بشن.
اینطوری کلی در نظر گرفتن ظرفیت نقالهها به معنی در نظر نگرفتن شرایط سوال هست و همینطور اینکه مثلا اگر ۲نقاله به ظرفیتهای ۵ و ۱ هم داشتیم بازهم ظرفیت نقالهها ۶ میشد ولی میبینید که این حالت جز شرایط صورت مسئله نیست
۰
ارسال: #۱۰
RE: سری دوم سوالات
ارسال: #۱۱
RE: سری دوم سوالات
(۱۸ مرداد ۱۳۹۰ ۱۰:۵۰ ب.ظ)Mile Stone نوشته شده توسط:خب نه دیگه تا اینجای ماجرا که گفتید درست، به c(10,5 طریق ۵ نفر برای تیم A انتخاب میشه و بقیه تیم B میشوند حالا باید یک بار هم این حالت را درنظر بگیریم که افرادی که در تیم A بودند در تیم B قرار بگیرند و افرادی که در تیم B بودند در تیم A در واقع باید جایگشت گروههای انتخاب شده را هم حساب کنیم چون دو تیم مجزا و نامساوی هستند ولی در این سوال دو گروه مساوی هستند و هر گروهی در هرتیمی قرار گیرد تفاوتی نمیکند.(18 مرداد ۱۳۹۰ ۱۰:۳۳ ب.ظ)narges_r نوشته شده توسط: فکر میکنم برای سوال اول اگر در سوال مطرح شده بود که ۱۰ نفر را میخواهیم در دو گروه مجزا مثلا اول و دوم تقسیم کنیم جواب !۲*c(10,5اگر دو تیم مجزای A,B داشته باشیم ؛ به c(10,5 طریق ۵ نفر برای تیم A انتخاب میکنیم و بقیه(۵ نفر باقیمانده) تیم B میشوند
۰
ارسال: #۱۲
RE: سری دوم سوالات
فرض کنید تعداد افراد ۴ نفر باشند و بخواهیم به دو گروه مساوی تقسیم کنیم:
A,B,C,D
حالت های ممکن:
AB,CD
CD,AB(تکراری)
AC,BD
BD,AC(تکراری)
BC,AD
AD,BC(تکراری)
تعداد حالات: [tex]\frac{\binom{4}{2}\binom{2}{2}}{2!}=\frac{6}{2}=3[/tex]
چون از هر دو حالت فقط به یکی از آنها احتیاج داریم پس تقسیم بر ۲ می کنیم.
در حالت کلی اگر تعداد گروهها K بود.جایگشت گروه های انتخاب شده(!K) حالات تکراری هستند و چون فقط به یک حالت از این تعداد نیاز داریم پس تقسیم بر !K می کنیم.
A,B,C,D
حالت های ممکن:
AB,CD
CD,AB(تکراری)
AC,BD
BD,AC(تکراری)
BC,AD
AD,BC(تکراری)
تعداد حالات: [tex]\frac{\binom{4}{2}\binom{2}{2}}{2!}=\frac{6}{2}=3[/tex]
چون از هر دو حالت فقط به یکی از آنها احتیاج داریم پس تقسیم بر ۲ می کنیم.
در حالت کلی اگر تعداد گروهها K بود.جایگشت گروه های انتخاب شده(!K) حالات تکراری هستند و چون فقط به یک حالت از این تعداد نیاز داریم پس تقسیم بر !K می کنیم.
ارسال: #۱۳
RE: سری دوم سوالات
(۱۹ مرداد ۱۳۹۰ ۰۹:۵۲ ق.ظ)**sara** نوشته شده توسط: فرض کنید تعداد افراد ۴ نفر باشند و بخواهیم به دو گروه مساوی تقسیم کنیم:
A,B,C,D
حالت های ممکن:
AB,CD
CD,AB(تکراری)
AC,BD
BD,AC(تکراری)
BC,AD
AD,BC(تکراری)
تعداد حالات: [tex]\frac{\binom{4}{2}\binom{2}{2}}{2!}=\frac{6}{2}=3[/tex]
چون از هر دو حالت فقط به یکی از آنها احتیاج داریم پس تقسیم بر ۲ می کنیم.
در حالت کلی اگر تعداد گروهها K بود.جایگشت گروه های انتخاب شده(!K) حالات تکراری هستند و چون فقط به یک حالت از این تعداد نیاز داریم پس تقسیم بر !K می کنیم.
این یعنی وقتی c(10,5 حساب میکنیم در واقع داریم تقسیم ۱۰ نفر بصورت دو گروه ۵نفره در دو گروه مجزا را حساب میکنیم و الان که در صورت سوال ذکر کرده دو گروه مساوی هستند باید بر فاکتوریل تعداد گروهها تقسیم کنیم؟
۰
ارسال: #۱۴
RE: سری دوم سوالات
(۱۸ مرداد ۱۳۹۰ ۰۱:۰۳ ق.ظ)ehsan_nekooee نوشته شده توسط: در کل ۶ تا ظرفیت برای اسکی بازها داریم و ۴ اسکی باز که می خوان سوار این نقالهها بشن. فک کنم اینطوری بشه
۱۵=(C(6,4
در کل ۶ ظرفیت داریم ولی در این شمارش نقالهها با هم متفاوتند پس مطمنیم که جواب از ۱۵ بیشتره و میشه با جواب شما حذف گزینه کرد .
(۱۸ مرداد ۱۳۹۰ ۰۱:۰۳ ق.ظ)ehsan_nekooee نوشته شده توسط: ظاهرا رنگ توپها نقشی در حل نداره. خب ۲n تا توپ داریم بخوایم n تا شو برداریم میشه:
(C(2n,n
درسته اگه توپهای سفید متمایز از هم باشند(و سیاه هم)
(۱۸ مرداد ۱۳۹۰ ۰۱:۰۳ ق.ظ)ehsan_nekooee نوشته شده توسط: برای این سوال یه راه حل دیگه هم به ذهنم میرسه. نمیدونم کدومش درسته.
۲n * 2n-1 * 2n-2 * 2n -3 * .... * n+1
این راه حل هم همون قبلیه و چون ترتیب برامون مهم نیست باید کلش بر !n تقسیم بشه
اگر توپهای سفید با هم یکسان باشند(و همینطور سیاه) n+1 حالت انتخاب داریم:
همه سیاه/یک سفید بقیه سیاه/....../n سفید
۰
ارسال: #۱۵
سری دوم سوالات
کاربر summer-66 کاملا" درست میگویند. باید توجه کنید که معمولا" وقتی طراح میخواد بگوید دو گروه با هم فرق میکنند روی دو گروه اسم میگذاره مثلا" میگوید تیم A و تیم B.
۰
ارسال: #۱۶
سری دوم سوالات
متوجه سوال شدم که دو تیم یکسان هستند و دو تیم باهم فرق ندارند فقط برام سوال پیش امد که اگر در سوال مطرح شده بود دوتیم باهم متفاوت هستند چه اتفاقی می افتاد؟!
پس نباید به !۲ تقسیم کنیم!من هم از اول همینو گفتم دیگه!!!
(۱۹ مرداد ۱۳۹۰ ۱۰:۵۶ ب.ظ)summer_66 نوشته شده توسط:(19 مرداد ۱۳۹۰ ۱۰:۰۹ ب.ظ)narges_r نوشته شده توسط: این یعنی وقتی c(10,5 حساب میکنیم در واقع داریم تقسیم ۱۰ نفر بصورت دو گروه ۵نفره در دو گروه مجزا را حساب میکنیم و الان که در صورت سوال ذکر کرده دو گروه مساوی هستند باید بر فاکتوریل تعداد گروهها تقسیم کنیم؟
نه.....
.... البته اگه طراح در نظرش گروهها از هم متمایز باشن اونوقت نباید تقسیم به دو کنیم البته این احتمال تقریبا صفره چون گفته فقط میخوان بازی کنن نگفته مسابقات جام جهانیه!!!!!!!!!!!!
پس نباید به !۲ تقسیم کنیم!من هم از اول همینو گفتم دیگه!!!
ارسال: #۱۷
RE: سری دوم سوالات
(۱۹ مرداد ۱۳۹۰ ۱۱:۲۶ ب.ظ)narges_r نوشته شده توسط: متوجه سوال شدم که دو تیم یکسان هستند و دو تیم باهم فرق ندارند فقط برام سوال پیش امد که اگر در سوال مطرح شده بود دوتیم باهم متفاوت هستند چه اتفاقی می افتاد؟!
(۱۹ مرداد ۱۳۹۰ ۱۰:۵۶ ب.ظ)summer_66 نوشته شده توسط:(19 مرداد ۱۳۹۰ ۱۰:۰۹ ب.ظ)narges_r نوشته شده توسط: این یعنی وقتی c(10,5 حساب میکنیم در واقع داریم تقسیم ۱۰ نفر بصورت دو گروه ۵نفره در دو گروه مجزا را حساب میکنیم و الان که در صورت سوال ذکر کرده دو گروه مساوی هستند باید بر فاکتوریل تعداد گروهها تقسیم کنیم؟
نه.....
.... البته اگه طراح در نظرش گروهها از هم متمایز باشن اونوقت نباید تقسیم به دو کنیم البته این احتمال تقریبا صفره چون گفته فقط میخوان بازی کنن نگفته مسابقات جام جهانیه!!!!!!!!!!!!
پس نباید به !۲ تقسیم کنیم!من هم از اول همینو گفتم دیگه!!!
اصلا"!۲ وقتی وارد ماجرا میشه که دو تیم یا دو گروه فرقی با هم نداشته باشند. یعنی اگه ده نفر به دو تیم الف و ب تقسیم بشوند جواب همان ترتیب ۵ از ده است..یا تعداد حالات انتخاب ۵ نفر از ده نفر. حالا اگه دو تیم اسمی نداشته باشند در محاسبه بالا یک تقسیم بر ۲ یا !۲ داریم چون حالاتی که دو تیم جابجا میشوند حالت جدیدی ایجاد نمیکنه. یعنی اگه A,B,C,D,Eدر تیم اول انتخاب شوند نتیجه میشه که F,G,H,I,Jبرای تیم دوم انتخاب بشوند. حالا یک حالت هم F,G,H,I,Jبرای تیم اول انتخاب میشوند و پنج نفر A,B,C,D,Eمیروند تیم دوم. اگه تیمها اسم نداشته باشند این دو حالت یکی است.
این قاعده کلی است یعنی اگه میخواستیم ۹ نفر را به سه تیم سه نفره تقسیم کنیم جواب بصورت زیر میشد:
(هر کار کردم نشد این برنامه فرمول نویسی را بالا بیارم.
 D
D

۰
ارسال: #۱۸
سری دوم سوالات
با سلام و عرض پوزش بخاطر جواب دادن به ارسالی که چند ماه پیش مطرح شده بود و تشکر از دوستان بخاطر طرح و پاسخگویی، خواستم بگم توی جواب ۲تا سوال میخام بحث کنم:
سوال ۲:
نمیدونم چرا کسی برای این سوال توضیحی نداد. به نظر سوال ساده ای میاد ولی بخاطر جواب ندادن بچهها به شک افتادم.. انتخاب ۳ از ۱۰ برای رئوس مثلث.
سوال ۵:
به نظرم اگه جواب سوال بخاد n از ۲n باشه باید ۲n رنگ مهره مختلف داشته باشیم. به نظرم جواب میشه n+1.
چون n+1 حالت بین ۰ تا n برای مهره های سیاه داریم و به ازای هرکدوم از حالات فقط ۱ حالت برای سفید.
سوال ۲:
نمیدونم چرا کسی برای این سوال توضیحی نداد. به نظر سوال ساده ای میاد ولی بخاطر جواب ندادن بچهها به شک افتادم.. انتخاب ۳ از ۱۰ برای رئوس مثلث.
سوال ۵:
به نظرم اگه جواب سوال بخاد n از ۲n باشه باید ۲n رنگ مهره مختلف داشته باشیم. به نظرم جواب میشه n+1.
چون n+1 حالت بین ۰ تا n برای مهره های سیاه داریم و به ازای هرکدوم از حالات فقط ۱ حالت برای سفید.
Can I see some ID?
Feeling left out?
نگران نباش، فقط روی این لینک برای ثبت نام کلیک کن. رمزت رو فراموش کردی؟ اینجا به یادت میاریم! close

