۰
subtitle
ارسال: #۱
سوال در مورد مرتبه زمانی
دو تا سوال هست که هر دو مثل همه و به نظر من جوابشون باید nlognبشه
بر اساس قضیه مستر اگه درجه ی f(n) از n به توان لگاریتم a در مبنای b بیشتر باشه تی ان برابر با تتای f(n) میشه
اما توی این دو مسأله برابر f(n)*logn شده. یعنی در حالتی که طبق مستر f(n) و n به توان لگاریتم هم درجه باشند
ممنون میشم کسی راهنمایی کنه
خیلی مهمه این سبک سوالات
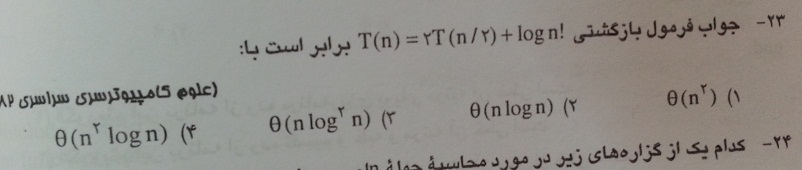

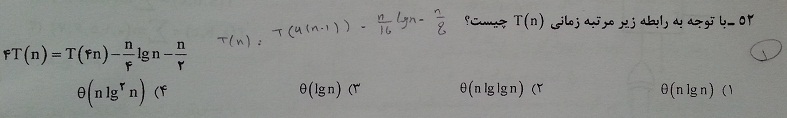
بر اساس قضیه مستر اگه درجه ی f(n) از n به توان لگاریتم a در مبنای b بیشتر باشه تی ان برابر با تتای f(n) میشه
اما توی این دو مسأله برابر f(n)*logn شده. یعنی در حالتی که طبق مستر f(n) و n به توان لگاریتم هم درجه باشند
ممنون میشم کسی راهنمایی کنه
خیلی مهمه این سبک سوالات
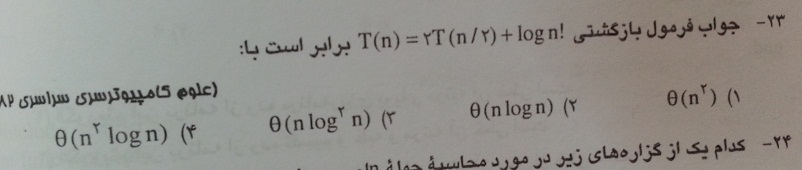

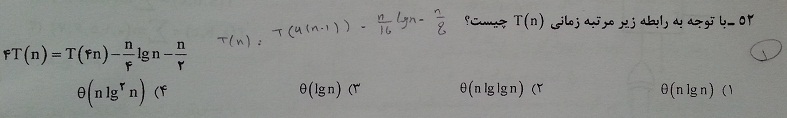
۰
ارسال: #۲
RE: سوال در مورد مرتبه زمانی
(۱۵ بهمن ۱۳۹۲ ۰۶:۴۶ ب.ظ)mj.net نوشته شده توسط: دو تا سوال هست که هر دو مثل همه و به نظر من جوابشون باید nlognبشه
بر اساس قضیه مستر اگه درجه ی f(n) از n به توان لگاریتم a در مبنای b بیشتر باشه تی ان برابر با تتای f(n) میشه
اما توی این دو مسأله برابر f(n)*logn شده. یعنی در حالتی که طبق مستر f(n) و n به توان لگاریتم هم درجه باشند
ممنون میشم کسی راهنمایی کنه
خیلی مهمه این سبک سوالات
مجبور شدم لپ تاپو بچرخونم سوالتونو بخونم !! چرا برعکسه!

به نظرم اولی میشه nlogn (لگاریتم به نمای دو).
----------------------
کلا هر وقت اختلاف بین فرمول مستر و fn تو یه log باشه ، میشه همون fn ولی به توان log یه واحد اضافه میشه.
----------------------
اصلاح میکنم . من ندیدم نوشته ۴Tn . دومی هم میشه به نظرم nlogn (لگاریتم به نمای دو).
۰
ارسال: #۳
RE: سوال در مورد مرتبه زمانی
(۱۵ بهمن ۱۳۹۲ ۰۶:۴۶ ب.ظ)mj.net نوشته شده توسط: دو تا سوال هست که هر دو مثل همه و به نظر من جوابشون باید nlognبشهسوال اول که مشخصه [tex]n(logn)^2[/tex] میشه. چون قسمت اول رابطه n میشه و قسمت دوم !logn برابر هست که با nlogn یکسانه و چون در یک logn با هم تفاوت دارند پس باید یه log به عبارت نهایی اضافه کرد و میشه [tex]n(logn)^2[/tex]
بر اساس قضیه مستر اگه درجه ی f(n) از n به توان لگاریتم a در مبنای b بیشتر باشه تی ان برابر با تتای f(n) میشه
اما توی این دو مسأله برابر f(n)*logn شده. یعنی در حالتی که طبق مستر f(n) و n به توان لگاریتم هم درجه باشند
ممنون میشم کسی راهنمایی کنه
خیلی مهمه این سبک سوالات
-----------------------------------------------
بعد از دیدن عکس عمودی به صورت افقی ، متوجه شدیم که رابطه سوال چیز دیگری است . و مورد دوم هم مثل مورد اول میباشد
ارسال: #۴
RE: سوال در مورد مرتبه زمانی
(۱۶ بهمن ۱۳۹۲ ۰۹:۱۷ ق.ظ)masoud67 نوشته شده توسط:شرطی که برای fn تو مستر وجود داره چیه؟(15 بهمن ۱۳۹۲ ۰۶:۴۶ ب.ظ)mj.net نوشته شده توسط: دو تا سوال هست که هر دو مثل همه و به نظر من جوابشون باید nlognبشهسوال اول که مشخصه [tex]n(logn)^2[/tex] میشه. چون قسمت اول رابطه n میشه و قسمت دوم !logn برابر هست که با nlogn یکسانه و چون در یک logn با هم تفاوت دارند پس باید یه log به عبارت نهایی اضافه کرد و میشه [tex]n(logn)^2[/tex]
بر اساس قضیه مستر اگه درجه ی f(n) از n به توان لگاریتم a در مبنای b بیشتر باشه تی ان برابر با تتای f(n) میشه
اما توی این دو مسأله برابر f(n)*logn شده. یعنی در حالتی که طبق مستر f(n) و n به توان لگاریتم هم درجه باشند
ممنون میشم کسی راهنمایی کنه
خیلی مهمه این سبک سوالات
در مورد دومی که استفاده از مستر جایز نیست و فکر کنم مرتبه اش بشه [tex]O(n)[/tex] چون داره به صورت خطی در هر مرحله مقدار n یه دونه کم میشه
ارسال: #۵
RE: سوال در مورد مرتبه زمانی
ارسال: #۶
RE: سوال در مورد مرتبه زمانی
(۱۶ بهمن ۱۳۹۲ ۰۹:۴۰ ق.ظ)masoud67 نوشته شده توسط:من قبل از شما یه جوابی دادم اون بالا!(16 بهمن ۱۳۹۲ ۰۹:۲۶ ق.ظ)e.shrm نوشته شده توسط: شرطی که برای fn تو مستر وجود داره چیه؟این Tex باز گیج شد و نشد فرمول بنویسم ولی خوش یمن بود چون رفتم از تو یه فایل عکس بردارم و بذارم ، زیرش دقیقا همین مثال رو گذاشته بود
اما اگه در مورد دومی منظورتونه که کلا با اصل مستر فرق داره و از اون روش حل نمیشه
اولی که بدیهیه.
برای دومی که گفتید مستر نمیشه.
چرا نمیشه گفت بخش fn به طور کلی از مرتبه nlogn هست (حد بالا) و بعد از مستر استفاده کرد؟
۰
۰
ارسال: #۸
RE: سوال در مورد مرتبه زمانی
(۱۵ بهمن ۱۳۹۲ ۰۶:۴۶ ب.ظ)mj.net نوشته شده توسط: دو تا سوال هست که هر دو مثل همه و به نظر من جوابشون باید nlognبشهتو عکس سومی دقیقا رابطه چیه ؟ اگه مرتبه را بخواد که این چیزی که شما نوشتی داره به صورت نمایی زیاد میشه
بر اساس قضیه مستر اگه درجه ی f(n) از n به توان لگاریتم a در مبنای b بیشتر باشه تی ان برابر با تتای f(n) میشه
اما توی این دو مسأله برابر f(n)*logn شده. یعنی در حالتی که طبق مستر f(n) و n به توان لگاریتم هم درجه باشند
ممنون میشم کسی راهنمایی کنه
خیلی مهمه این سبک سوالات
اگر زمان اجراشو میخواسته (که من اشتباها فرض را بر این گذاشتم) میشه مرتبه n
(۱۶ بهمن ۱۳۹۲ ۰۹:۵۵ ق.ظ)e.shrm نوشته شده توسط:آخه تو عکس سومی ایشون نوشته T(n)= T(4(n-1)) + n/16*Logn + n/2(16 بهمن ۱۳۹۲ ۰۹:۴۰ ق.ظ)masoud67 نوشته شده توسط:من قبل از شما یه جوابی دادم اون بالا!(16 بهمن ۱۳۹۲ ۰۹:۲۶ ق.ظ)e.shrm نوشته شده توسط: شرطی که برای fn تو مستر وجود داره چیه؟این Tex باز گیج شد و نشد فرمول بنویسم ولی خوش یمن بود چون رفتم از تو یه فایل عکس بردارم و بذارم ، زیرش دقیقا همین مثال رو گذاشته بود
اما اگه در مورد دومی منظورتونه که کلا با اصل مستر فرق داره و از اون روش حل نمیشه
اولی که بدیهیه.
برای دومی که گفتید مستر نمیشه.
چرا نمیشه گفت بخش fn به طور کلی از مرتبه nlogn هست (حد بالا) و بعد از مستر استفاده کرد؟
مستر اصلا چنین رابطه ای را حل نمیکنه. اینو نمیدونم از چه رابطه ای باید حل کرد چون اگر مقدار گذاری کنید ، تابع فقط داره زیاد میشه و رشد نمایی داره
اونی که گفتم میشه n منظورم زمان اجراش بود نه مرتبه الگوریتم.
اگه چیزی که شما میگید مستر این رابطه را چی میده
T(n) = T(n-1) + n
مرتبه الگوریتم این میشه n^2 . ولی با چیزی که شما گفتید مرتبه اش باید بشه nlogn
ارسال: #۹
RE: سوال در مورد مرتبه زمانی
(۱۶ بهمن ۱۳۹۲ ۰۹:۵۷ ق.ظ)masoud67 نوشته شده توسط:--------------------(16 بهمن ۱۳۹۲ ۰۹:۵۵ ق.ظ)e.shrm نوشته شده توسط:آخه تو عکس سومی ایشون نوشته T(n)= T(4(n-1)) + n/16*Logn + n/2(16 بهمن ۱۳۹۲ ۰۹:۴۰ ق.ظ)masoud67 نوشته شده توسط:من قبل از شما یه جوابی دادم اون بالا!(16 بهمن ۱۳۹۲ ۰۹:۲۶ ق.ظ)e.shrm نوشته شده توسط: شرطی که برای fn تو مستر وجود داره چیه؟این Tex باز گیج شد و نشد فرمول بنویسم ولی خوش یمن بود چون رفتم از تو یه فایل عکس بردارم و بذارم ، زیرش دقیقا همین مثال رو گذاشته بود
اما اگه در مورد دومی منظورتونه که کلا با اصل مستر فرق داره و از اون روش حل نمیشه
اولی که بدیهیه.
برای دومی که گفتید مستر نمیشه.
چرا نمیشه گفت بخش fn به طور کلی از مرتبه nlogn هست (حد بالا) و بعد از مستر استفاده کرد؟
مستر اصلا چنین رابطه ای را حل نمیکنه. اینو نمیدونم از چه رابطه ای باید حل کرد چون اگر مقدار گذاری کنید ، تابع فقط داره زیاد میشه و رشد نمایی داره
اونی که گفتم میشه n منظورم زمان اجراش بود نه مرتبه الگوریتم.
اگه چیزی که شما میگید مستر این رابطه را چی میده
T(n) = T(n-1) + n
مرتبه الگوریتم این میشه n^2 . ولی با چیزی که شما گفتید مرتبه اش باید بشه nlogn
اونی که شما جواب دادید راه حل خودشونه! نه صورت مساله. صورت مساله یک کم پایین تره!
ارسال: #۱۰
RE: سوال در مورد مرتبه زمانی
۰
ارسال: #۱۱
RE: سوال در مورد مرتبه زمانی
ظاهرا پست های دیشب همه پاک شده چون من دیشب جواب دادم
هر دو سوال از این قضیه استفاده کردن
تبصره در قضیه اصلی:
اگه رابطه بازگشتی بصورت زیر باشه :
[tex]T(n)=aT(\frac{n}{b}) n^{log_{b}^{a}}*logn^{d}[/tex]
اونوقت حاصل میشه :
[tex]n^{log_{b}^{a}}*log^{d 1}[/tex]
همون fn فقط به توان لگاریتمش(d) یه واحد اضافه میشه
هر دو سوال از این قضیه استفاده کردن
تبصره در قضیه اصلی:
اگه رابطه بازگشتی بصورت زیر باشه :
[tex]T(n)=aT(\frac{n}{b}) n^{log_{b}^{a}}*logn^{d}[/tex]
اونوقت حاصل میشه :
[tex]n^{log_{b}^{a}}*log^{d 1}[/tex]
همون fn فقط به توان لگاریتمش(d) یه واحد اضافه میشه
۰
ارسال: #۱۲
RE: سوال در مورد مرتبه زمانی
سلام به همگی
من نمیدونم چرا عکسا کج شدن :دی
مریم.راز دیشب جواب داد و منم جواب دادم. پاک شده
ممنون از همگی
این رابطه رو توی مستر من بلد نبودم. مستر دیگه چی داره که من بلد نیستم ؟
فقط همون سه حالت کمتر مساوی بیشتر و میدونم ازش
عکس سوم هم همون سوال پارسه هست تو ۱۰۰ دوم. وقتی تبدیلش کرده به شکل مستر در میاد.
فقط یه سوال دیگه که اگه [tex]aT\left ( n/b - 1 \right ) f\left ( n \right )[/tex] باشه دیگه مستر نیست ؟
ممنون ... فقط توی لگاریتم جای a و b عوض شده. اشتباه لپیه
دیشب این و سوال کرده بودم که دوستان زحمت کشیدن عکسش رو گذاشتن
نمیدونم چرا برعکس شده. فقط شما چرا لپتاپ و چرخوندی ؟؟؟ خوب عکس و سیو میکردی
جا داره یادی از پت و مت عزیز بکنیم
بازم ممنون
من نمیدونم چرا عکسا کج شدن :دی
مریم.راز دیشب جواب داد و منم جواب دادم. پاک شده
ممنون از همگی
این رابطه رو توی مستر من بلد نبودم. مستر دیگه چی داره که من بلد نیستم ؟

فقط همون سه حالت کمتر مساوی بیشتر و میدونم ازش
عکس سوم هم همون سوال پارسه هست تو ۱۰۰ دوم. وقتی تبدیلش کرده به شکل مستر در میاد.
فقط یه سوال دیگه که اگه [tex]aT\left ( n/b - 1 \right ) f\left ( n \right )[/tex] باشه دیگه مستر نیست ؟
(۱۶ بهمن ۱۳۹۲ ۰۲:۴۵ ب.ظ)maryam.raz نوشته شده توسط: اگه رابطه بازگشتی بصورت زیر باشه :
[tex]T(n)=aT(\frac{n}{b}) n^{log_{a}^{b}}*logn^{d}[/tex]
اونوقت حاصل میشه :
[tex]n^{log_{a}^{b}}*log^{d 1}[/tex]
ممنون ... فقط توی لگاریتم جای a و b عوض شده. اشتباه لپیه
دیشب این و سوال کرده بودم که دوستان زحمت کشیدن عکسش رو گذاشتن
(۱۶ بهمن ۱۳۹۲ ۰۸:۴۲ ق.ظ)e.shrm نوشته شده توسط: مجبور شدم لپ تاپو بچرخونم سوالتونو بخونم !! چرا برعکسه!
نمیدونم چرا برعکس شده. فقط شما چرا لپتاپ و چرخوندی ؟؟؟ خوب عکس و سیو میکردی

جا داره یادی از پت و مت عزیز بکنیم
بازم ممنون

ارسال: #۱۳
RE: سوال در مورد مرتبه زمانی
(۱۶ بهمن ۱۳۹۲ ۱۱:۵۷ ب.ظ)mj.net نوشته شده توسط: ممنون ... فقط توی لگاریتم جای a و b عوض شده. اشتباه لپیهمن که رابطه دیگه ای بلد نیستم از مستر
دیشب این و سوال کرده بودم که دوستان زحمت کشیدن عکسش رو گذاشتن
نمیدونم چرا برعکس شده. فقط شما چرا لپتاپ و چرخوندی ؟؟؟ خوب عکس و سیو میکردی
جا داره یادی از پت و مت عزیز بکنیم
بازم ممنون
درستش کردم فرمولو. از بس این فرمول نویسی قات داشت هزار بار نوشتم دیگه خودمم قاتی کردم

Can I see some ID?
Feeling left out?
نگران نباش، فقط روی این لینک برای ثبت نام کلیک کن. رمزت رو فراموش کردی؟ اینجا به یادت میاریم! close



