۰
subtitle
ارسال: #۱
پیچیدگی زمانی ۳ قطعه کد تقریبا مشابه!
سلام
کتاب پوران پژوهش یه مثال داره که فکرمو خیلی مشغول کرده
در هر سه کد تعداد اجرای خط x=x+1 را بدست میاورد.
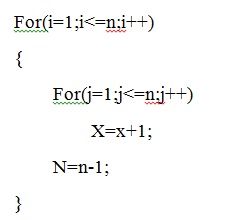
[tex]n n-1 n-2 ... (n-\frac{n}{2} 1)=\frac{3n^{2} 2n}{8}=\Theta (n^{2})[/tex]
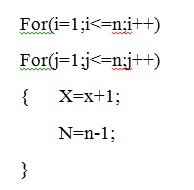
[tex]\frac{n}{2} \frac{n}{4} \frac{n}{8} ...=n*\frac{\frac{1}{2}}{1-\frac{1}{2}}=\Theta (n)[/tex]

[tex]n \frac{n}{2} \frac{n}{4} \frac{n}{8} ... \frac{n}{n}=\Theta (nlogn)[/tex]

کتاب پوران پژوهش یه مثال داره که فکرمو خیلی مشغول کرده

در هر سه کد تعداد اجرای خط x=x+1 را بدست میاورد.
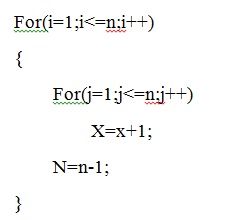
[tex]n n-1 n-2 ... (n-\frac{n}{2} 1)=\frac{3n^{2} 2n}{8}=\Theta (n^{2})[/tex]
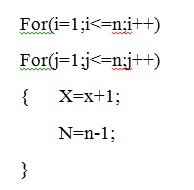
[tex]\frac{n}{2} \frac{n}{4} \frac{n}{8} ...=n*\frac{\frac{1}{2}}{1-\frac{1}{2}}=\Theta (n)[/tex]

[tex]n \frac{n}{2} \frac{n}{4} \frac{n}{8} ... \frac{n}{n}=\Theta (nlogn)[/tex]

۰
ارسال: #۲
RE: پیچیدگی زمانی ۳ قطعه کد تقریبا مشابه!
پیرو فرمایشات دوستان من هم یه چیزایی میگم:
اولین سوال که همونطور که نوشتید یه تصاعد حسابی هست که جمله اولش برابر n و جمله آخرش برابر ([tex]n- \frac{n}{2} 1[/tex]) و برای محاسبه تصاعد حسابی باید جمله اول و آخر رو جمع کنید و در [tex]\frac{n}{2}[/tex] ضرب کنید (که n تعداد جملات تصاعد است و در اینجا برابر است با [tex]\frac{n}{2}[/tex] که در کل میشود [tex]\frac{n}{4}[/tex])!
جمله آخر که در واقع برابر است با [tex]\frac{2n -n 2}{2}[/tex] که همون [tex]\frac{n 2}{2}[/tex] است و بعد از جمع با n برابر میشه با [tex]\frac{3n 2}{2}[/tex] و بعد از ضرب در [tex]\frac{n}{4}[/tex] میشه همون که شما گفتید.
سوال ۲ :
این هم مثل سوال قبل اگه هر مرحله تعداد اجرای جمله اصلی رو در نظر بگیرید میشه همون [tex]\frac{n}{2} \frac{n}{4} ...[/tex] وقتی از n فاکتور بگیریم به [tex]n(\frac{1}{2} \frac{1}{4} ...)[/tex] میرسیم . خوب جمله داخل پرانتز یه تصاعد هندسی با جمله اول [tex]\frac{1}{2}[/tex] و قدرنسبت [tex]\frac{1}{2}[/tex] است و برای محاسبه تصاعد هندسی وقتی که جملات کوچکتر از ۱ هستند و تعداد آنها بینهایت است از فرمول :
جمله اول تقسیم بر ۱منهای قدر نسبت استفاده میکنیم. که در این سوال میشه [tex]\frac{\frac{1}{2} }{1-\frac{1}{2} }[/tex] که برابر با ۱ است و n*1 بدست می آید.
سوال ۳:
حلقه داخلی با گام i هست که در اون صورت داریم :
دور اول چون i برابر ۱ هست حلقه داخلی n بار اجرا میشه دور دوم چون i برابر ۲ است حلقه داخلی با شمارنده فرد اجرا میشود(۱و۳و۵و...n) (که میشه [tex]\frac{n}{2}[/tex]بار) و به همین ترتیب تا آخر . که در کل میشه [tex]n \frac{n}{2} \frac{n}{3} ...[/tex] و با فاکتور گرفتن از n بدست میاد [tex]n(1 \frac{1}{2} \frac{1}{3} ...)[/tex] که [tex](1 \frac{1}{2} \frac{1}{3} ...)[/tex] تقریبا برابر با [tex]Lg(n)[/tex](نه دقیقا اما در کل میشه گفت که هم رشد هستند) پس در کل میگیم این الگوریتم از مرتبه [tex]\Theta( nlgn)[/tex].
اولین سوال که همونطور که نوشتید یه تصاعد حسابی هست که جمله اولش برابر n و جمله آخرش برابر ([tex]n- \frac{n}{2} 1[/tex]) و برای محاسبه تصاعد حسابی باید جمله اول و آخر رو جمع کنید و در [tex]\frac{n}{2}[/tex] ضرب کنید (که n تعداد جملات تصاعد است و در اینجا برابر است با [tex]\frac{n}{2}[/tex] که در کل میشود [tex]\frac{n}{4}[/tex])!
جمله آخر که در واقع برابر است با [tex]\frac{2n -n 2}{2}[/tex] که همون [tex]\frac{n 2}{2}[/tex] است و بعد از جمع با n برابر میشه با [tex]\frac{3n 2}{2}[/tex] و بعد از ضرب در [tex]\frac{n}{4}[/tex] میشه همون که شما گفتید.
سوال ۲ :
این هم مثل سوال قبل اگه هر مرحله تعداد اجرای جمله اصلی رو در نظر بگیرید میشه همون [tex]\frac{n}{2} \frac{n}{4} ...[/tex] وقتی از n فاکتور بگیریم به [tex]n(\frac{1}{2} \frac{1}{4} ...)[/tex] میرسیم . خوب جمله داخل پرانتز یه تصاعد هندسی با جمله اول [tex]\frac{1}{2}[/tex] و قدرنسبت [tex]\frac{1}{2}[/tex] است و برای محاسبه تصاعد هندسی وقتی که جملات کوچکتر از ۱ هستند و تعداد آنها بینهایت است از فرمول :
جمله اول تقسیم بر ۱منهای قدر نسبت استفاده میکنیم. که در این سوال میشه [tex]\frac{\frac{1}{2} }{1-\frac{1}{2} }[/tex] که برابر با ۱ است و n*1 بدست می آید.
سوال ۳:
حلقه داخلی با گام i هست که در اون صورت داریم :
دور اول چون i برابر ۱ هست حلقه داخلی n بار اجرا میشه دور دوم چون i برابر ۲ است حلقه داخلی با شمارنده فرد اجرا میشود(۱و۳و۵و...n) (که میشه [tex]\frac{n}{2}[/tex]بار) و به همین ترتیب تا آخر . که در کل میشه [tex]n \frac{n}{2} \frac{n}{3} ...[/tex] و با فاکتور گرفتن از n بدست میاد [tex]n(1 \frac{1}{2} \frac{1}{3} ...)[/tex] که [tex](1 \frac{1}{2} \frac{1}{3} ...)[/tex] تقریبا برابر با [tex]Lg(n)[/tex](نه دقیقا اما در کل میشه گفت که هم رشد هستند) پس در کل میگیم این الگوریتم از مرتبه [tex]\Theta( nlgn)[/tex].
۰
۰
ارسال: #۴
RE: پیچیدگی زمانی ۳ قطعه کد تقریبا مشابه!
(۱۹ آبان ۱۳۹۱ ۱۱:۱۲ ق.ظ)m@hboobe نوشته شده توسط: سلام
کتاب پوران پژوهش یه مثال داره که فکرمو خیلی مشغول کرده
در هر سه کد تعداد اجرای خط x=x+1 را بدست میاورد.
[tex]n n-1 n-2 ... (n-\frac{n}{2} 1)=\frac{3n^{2} 2n}{8}=\Theta (n^{2})[/tex]
[tex]\frac{n}{2} \frac{n}{4} \frac{n}{8} ...=n*\frac{\frac{1}{2}}{1-\frac{1}{2}}=\Theta (n)[/tex]
[tex]n \frac{n}{2} \frac{n}{4} \frac{n}{8} ... \frac{n}{n}=\Theta (nlogn)[/tex]
سلام
اشتباه شما در این است که به بلوک ها توجه نمیکنید که کجا باز شده و کجا بسته شده ! منظورم از بلوک ها همان براکت هاست.
توجه دقیق تر به مسئله داشته باشید. (از لحاظ syntax این دو برنامه با هم فرق میکنند.)
۰
ارسال: #۵
RE: پیچیدگی زمانی ۳ قطعه کد تقریبا مشابه!
تو پیوست اولتو توجه کنین که چون جلوی حلقه for داخلی علامت بلوک یا همون آکولاد نذاشته پس فقط یه دستور جلوش متعلق به حلقه for داخلی هست و بعد از اتمام حلقه داخلی میاد بیرون بعد یکی از n کم می کنه و باز کارو ادامه می ده.
اما تو پیوست دوم بلوک متعلق به حلقه داخلی هست و به ازای هر بار اجرای حلقه داخلی یکی از مقدار n کم می شه.
پیوست سوم شما فکر کنم یه چیز رو ننوشتین چک کنین ببینین درسته؟
اما تو پیوست دوم بلوک متعلق به حلقه داخلی هست و به ازای هر بار اجرای حلقه داخلی یکی از مقدار n کم می شه.
پیوست سوم شما فکر کنم یه چیز رو ننوشتین چک کنین ببینین درسته؟
۰
۰
ارسال: #۷
پیچیدگی زمانی ۳ قطعه کد تقریبا مشابه!
ممنون از راهنمایی همتون
حواسم به بلوک ها هست اما یکم بی دقتی کردم !
با trace و مقداردهی n تقریبا یه چیزایی فهمیدم!
پ.ن:کلا با مسائل پارامتری رابطه نسبتا خوبی ندارم!
حواسم به بلوک ها هست اما یکم بی دقتی کردم !

با trace و مقداردهی n تقریبا یه چیزایی فهمیدم!
پ.ن:کلا با مسائل پارامتری رابطه نسبتا خوبی ندارم!
Can I see some ID?
Feeling left out?
نگران نباش، فقط روی این لینک برای ثبت نام کلیک کن. رمزت رو فراموش کردی؟ اینجا به یادت میاریم! close
