۰
subtitle
ارسال: #۱
[تست] تست ۳۷ آیتی ۸۷
به چند روش می توان ۸ رخ را درصفحه شطرنج قرار داد به طوریکه نسبت به قطر اصلی صفحه متقارن قرار گرفته و هیچ دو رخی یکدیگر را تهدید نکنند؟
۹۸۲
۷۶۴
۵۶۴
۲۳۲
۹۸۲
۷۶۴
۵۶۴
۲۳۲
۲
ارسال: #۲
RE: [تست] تست ۳۷ آیتی ۸۷
فرض می کنیم [tex]a_{n}[/tex] تعداد حالات چیدن n رخ در صفحه n x n با شرایط گفته شده، است.
[tex]a_{8}=? , a_{0}=1 , a_{1}=1 , a_{2}=2 ,a_{3}=4[/tex]
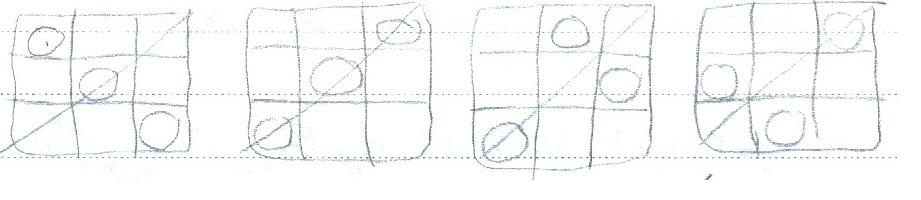
محدودیت ها: سطر و ستون رخها یکی نباشد و نسبت به قطر اصلی متقارن باشند.
حتماً در هر سطر باید یک رخ بگذاریم نه بیشتر و نه کمتر.
حالا دو حالت داریم یا رخ در قطر قرار بگیرد یا در خانه غیر قطر:
اگر رخ در هر خانه ای غیر از قطر برود [tex]a_{n-2}[/tex] حالت دارد.( [tex](n-2)\times (n-2)[/tex] خانه باقی می ماند.)
اگر رخ در قطر باشد [tex]a_{n-1}[/tex] حالت دارد.( [tex](n-1)\times (n-1)[/tex] خانه باقی می ماند.)
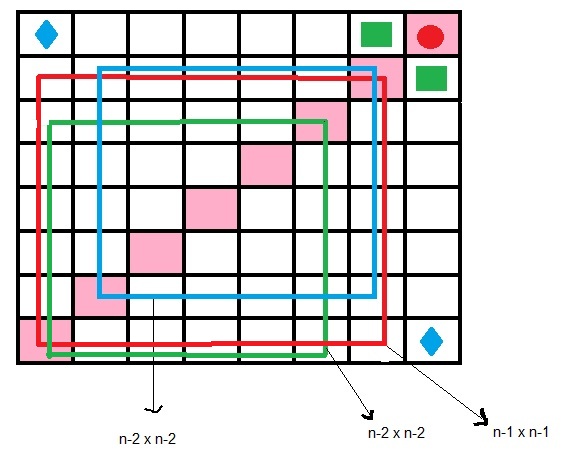
چون در هر سطر یک خانه عضو قطر داریم و [tex]n-1[/tex] خانه غیر قطر داریم، در نتیجه:
[tex]a_{n}=a_{n-1} (n-1)a_{n-2}[/tex]
جواب نهایی برای صفحه شطرنج [tex]8\times 8[/tex]:
[tex]a_{4}=a_{3} 3a_{2}=10[/tex]
[tex]a_{5}=a_{4} 4a_{3}=26[/tex]
[tex]a_{6}=a_{5} 5a_{4}=76[/tex]
[tex]a_{7}=a_{6} 6a_{5}=226[/tex]
[tex]a_{8}=a_{7} 7a_{6}=764[/tex]
جواب می شه گزینه ۲
بر اساس صدای کلاس آقای یوسفی
جلسه سوم قسمت دوم
[tex]a_{8}=? , a_{0}=1 , a_{1}=1 , a_{2}=2 ,a_{3}=4[/tex]

محدودیت ها: سطر و ستون رخها یکی نباشد و نسبت به قطر اصلی متقارن باشند.
حتماً در هر سطر باید یک رخ بگذاریم نه بیشتر و نه کمتر.
حالا دو حالت داریم یا رخ در قطر قرار بگیرد یا در خانه غیر قطر:
اگر رخ در هر خانه ای غیر از قطر برود [tex]a_{n-2}[/tex] حالت دارد.( [tex](n-2)\times (n-2)[/tex] خانه باقی می ماند.)
اگر رخ در قطر باشد [tex]a_{n-1}[/tex] حالت دارد.( [tex](n-1)\times (n-1)[/tex] خانه باقی می ماند.)

چون در هر سطر یک خانه عضو قطر داریم و [tex]n-1[/tex] خانه غیر قطر داریم، در نتیجه:
[tex]a_{n}=a_{n-1} (n-1)a_{n-2}[/tex]
جواب نهایی برای صفحه شطرنج [tex]8\times 8[/tex]:
[tex]a_{4}=a_{3} 3a_{2}=10[/tex]
[tex]a_{5}=a_{4} 4a_{3}=26[/tex]
[tex]a_{6}=a_{5} 5a_{4}=76[/tex]
[tex]a_{7}=a_{6} 6a_{5}=226[/tex]
[tex]a_{8}=a_{7} 7a_{6}=764[/tex]
جواب می شه گزینه ۲

بر اساس صدای کلاس آقای یوسفی
جلسه سوم قسمت دوم
۰
ارسال: #۳
RE: [تست] تست ۳۷ آیتی ۸۷
(۰۸ بهمن ۱۳۸۹ ۱۱:۰۷ ق.ظ)amir2930 نوشته شده توسط: به چند روش می توان ۸ رخ را درصفحه شطرنج قرار داد به طوریکه نسبت به قطر اصلی صفحه متقارن قرار گرفته و هیچ دو رخی یکدیگر را تهدید نکنند؟
۹۸۲
۷۶۴
۵۶۴
۲۳۲
بعضی سوالهای گسسته کنکور هیچکی نمیتونه حل کنه

فکر کنم طراحشم حلش نکرده
یکیش همینه
یکیش سواله ۱ گسسته IT88
۰
ارسال: #۴
[تست] تست ۳۷ آیتی ۸۷
ممنون سارا جان خیلی خوب توضیح دادی بی نهایت ممنون
فقط میشه بگی اگه این محدودیت رو نداشتیم آیا یه حالت بیشتر نداشتیم یعنی چه روی قطر میگذاشتیم چه غیر قطر فرقی نداشت ؟!
فقط میشه بگی اگه این محدودیت رو نداشتیم آیا یه حالت بیشتر نداشتیم یعنی چه روی قطر میگذاشتیم چه غیر قطر فرقی نداشت ؟!
ارسال: #۵
RE: [تست] تست ۳۷ آیتی ۸۷
(۱۹ بهمن ۱۳۸۹ ۱۱:۵۰ ب.ظ)afagh1389 نوشته شده توسط: ممنون سارا جان خیلی خوب توضیح دادی بی نهایت ممنونخواهش می کنم آفاق جان
فقط میشه بگی اگه این محدودیت رو نداشتیم آیا یه حالت بیشتر نداشتیم یعنی چه روی قطر میگذاشتیم چه غیر قطر فرقی نداشت ؟!
من دقیقاً چیزی رو که آقای یوسفی توی کلاسشون گفتن رو براتون توضیح دادم. آقای یوسفی واقعا مسائل رو خیلی جالب توضیح می دن و حل می کنن.
راستش این شکلی که براتون ضمیمه کرده بودم برای قطر فرعی بود

البته تفاوتی توی حل مسئله ایجاد نمی کنه.
برای قطر اصلی این شکلی می شه:
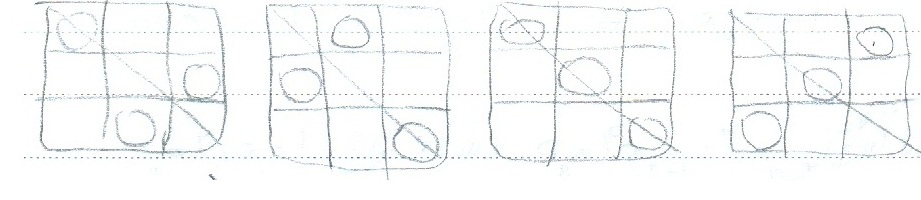
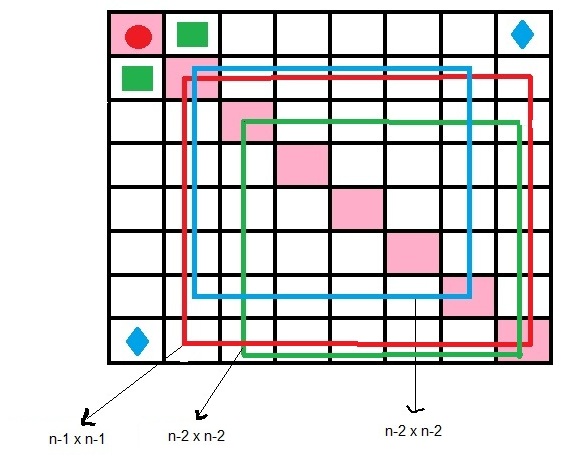
آفاق جان سوال شما اینه که اگر محدودیت متقارن بودن نسبت به قطر اصلی وجود نداشت مسئله چطور حل می شد؟
اگر منظورتون همینه، مسئله این طوری حل می شه:
فرض کنید اولین رخ رو می خواهیم در سطر اول قرار بدیم، پس n محل در سطر اول وجود داره که رخ اول می تونه در اون قرار بگیره.
حالا رخ دوم رو در سطر دوم قرار می دیم، چون یکی از ستونها توسط رخ قبلی اشغال شده پس n-1 محل در سطر دوم وجود داره که رخ دوم می تونه انتخاب کنه.
همینطور برای رخ سوم در سطر سوم n-2 محل برای انتخاب محل قرارگیری وجود داره.
...
تا می رسیم به رخ آخر که فقط یک انتخاب براش باقی مونده.
در نتیجه جواب سوال می شه !n
برای هشت رخ در صفحه شطرنج [tex]8\times 8[/tex]
!۸ روش وجود داره
روش دیگه حلش می شه:
فرض کنیم رخ اول رو در ستون اول سطر اول قرار بدیم، پس بقیه رخها رو در سطر اول و ستون اول نمی تونیم بگذاریم. در نتیجه یک صفحه [tex]n-1\times n-1[/tex] باقی می مونه.
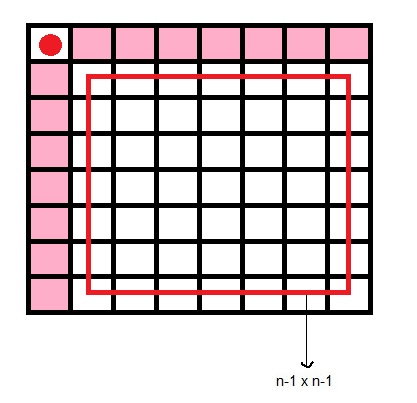
و چون در هر سطر n خانه قرار داره و محدودیتی برای انتخاب یکی از این خانهها نداریم در نتیجه:
[tex]a_{n}=n(a_{n-1})[/tex]
که این همون رابطه بازگشتی !n هست.
۰
Can I see some ID?
Feeling left out?
نگران نباش، فقط روی این لینک برای ثبت نام کلیک کن. رمزت رو فراموش کردی؟ اینجا به یادت میاریم! close

