۰
subtitle
ارسال: #۱
[نکات] کارآیی، تحلیل و مرتبه الگوریتمها - روابط بازگشتی
برای شروع:
نکته:
n^2+log n از مرتبه تتا n^2هست اماn^2*logn نه
نکته:
n^2+log n از مرتبه تتا n^2هست اماn^2*logn نه
۲
ارسال: #۲
RE: [نکات] کارآیی، تحلیل و مرتبه الگوریتمها - روابط بازگشتی
جواب هر رابطه بازگشتی به فرم [tex]T(n)=T(\alpha n) T((1-\alpha) n) \Theta (n)[/tex] به طوری که [tex]\alpha[/tex] یک عدد ثابت و در محدوده [tex]0<\alpha <1[/tex] است برابر است با [tex]T(n)=\Theta (nlgn)[/tex]
خیلی راحت میشه با درخت بازگشتی اثباتش کرد
خیلی راحت میشه با درخت بازگشتی اثباتش کرد
۰
ارسال: #۳
RE: [نکات] کارآیی، تحلیل و مرتبه الگوریتمها - روابط بازگشتی
یکی از تمرین های CLRS هست که توی کتاب یوسفی جوابش بود، به نظرم خیلی مفیده!
۱
۱
ارسال: #۵
RE: [نکات] کارآیی، تحلیل و مرتبه الگوریتمها - روابط بازگشتی
[tex]n^{k}=O((logn)^{logn})[/tex]
این رو یکجا خوندم ولی دلیلش رو نمیدونم اما فکر کنم عدد بگذارید دلیلش رو بفهمید!
این رو یکجا خوندم ولی دلیلش رو نمیدونم اما فکر کنم عدد بگذارید دلیلش رو بفهمید!
ارسال: #۶
RE: [نکات] کارآیی، تحلیل و مرتبه الگوریتمها - روابط بازگشتی
(۱۴ بهمن ۱۳۸۹ ۰۸:۵۵ ب.ظ)afagh1389 نوشته شده توسط: [tex]n^{k}=O((logn)^{logn})[/tex]
این رو یکجا خوندم ولی دلیلش رو نمیدونم اما فکر کنم عدد بگذارید دلیلش رو بفهمید!
با توجه به این نکته که: [tex]{\color{red} a}^{\log {\color{blue}b}}={\color{blue} b}^{\log {\color{red} a}}[/tex]
[tex]{\color{red} \log n}^{\log {\color{blue} n}}={\color{blue} n}^{\log {\color{red} \log n}}[/tex]
۱
ارسال: #۷
[نکات] کارآیی، تحلیل و مرتبه الگوریتمها - روابط بازگشتی
T(n)=2T(n/2)+nlogn
به عقیده من فرآیند جواب به این صورت میشه:
T(n/2)+T(n/2)+nlogn
پس در نهایت داریم:
n+nlogn
که میشه خود (O(nlogn
به عقیده من فرآیند جواب به این صورت میشه:
T(n/2)+T(n/2)+nlogn
پس در نهایت داریم:
n+nlogn
که میشه خود (O(nlogn
ارسال: #۸
RE: [نکات] کارآیی، تحلیل و مرتبه الگوریتمها - روابط بازگشتی
۰
ارسال: #۹
RE: نکات طراحی الگوریتم
[tex]T(n)=T(n-1) T(n-1)=2*T(n-1)\epsilon O(2^{n})[/tex]
که توی کتاب مقسمی اشتباها دومی رو از مرتبه (O(n گرفته!!!!
که توی کتاب مقسمی اشتباها دومی رو از مرتبه (O(n گرفته!!!!
۰
ارسال: #۱۰
RE: [نکات] پیچیدگی زمانی
برای حل رابطه بازگشتی از طریق درخت بازگشت به این نکته دقت کنید:
ارتفاع درخت (h) توسط فرمول
محاسبه میشود که در آن b اندازه زیر مسائل است.
یادآوری:
![[تصویر: attachment.php?aid=97]](https://manesht.ir/forum/attachment.php?aid=97)
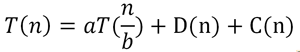
ارتفاع درخت (h) توسط فرمول

محاسبه میشود که در آن b اندازه زیر مسائل است.
یادآوری:
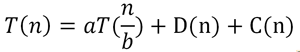
۰
ارسال: #۱۱
RE: [نکات] کارآیی، تحلیل و مرتبه الگوریتمها - روابط بازگشتی
به نکته ظریف زیر دقت کنید:
![[تصویر: attachment.php?aid=119]](https://manesht.ir/forum/attachment.php?aid=119)
------------------
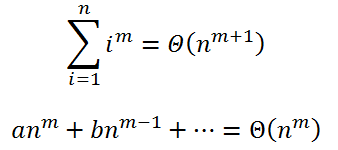
بچهها شما هم شرکت کنید دیگه
------------------
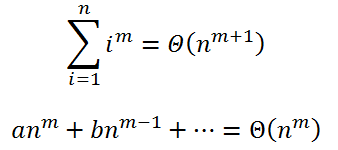
بچهها شما هم شرکت کنید دیگه

۰
ارسال: #۱۲
RE: [نکات] کارآیی، تحلیل و مرتبه الگوریتمها - روابط بازگشتی
یه نکته جالب برای حل روابط بازگشتی:
![[تصویر: attachment.php?aid=135]](https://manesht.ir/forum/attachment.php?aid=135)
![[تصویر: attachment.php?aid=136]](https://manesht.ir/forum/attachment.php?aid=136)
۰
ارسال: #۱۳
RE: [نکات] کارآیی، تحلیل و مرتبه الگوریتمها - روابط بازگشتی
تذکر: در این نکته o کوچک داریم. هر چند که برای O بزرگ هم صحیح هست . اما با o کوچک به این نکته پی میبریم که مقدار سمت چپ عبارت اکیداً کوچکتر هست.
۰
ارسال: #۱۴
RE: [نکات] کارآیی، تحلیل و مرتبه الگوریتمها - روابط بازگشتی
با سلا م به دوستان، یه فایل upload براتون کردم که سوالات دانشگاه MIT هست جواب هم کنارش هست . خیلی فوق العاده هست . حتماً حتماً حتماً دانلود کنید
مهمان عزیز شما قادر به مشاهده پیوندهای انجمن مانشت نمیباشید. جهت مشاهده پیوندها ثبت نام کنید.
مهمان عزیز شما قادر به مشاهده پیوندهای انجمن مانشت نمیباشید. جهت مشاهده پیوندها ثبت نام کنید.
۰
ارسال: #۱۵
RE: [نکات] کارآیی، تحلیل و مرتبه الگوریتمها - روابط بازگشتی
سلام . یه سوال جالب از جزوه سید جوادی( اگه بتونم نکات جالبش رو براتون میزارم)
برای ۴ خانه در نظر بگیرید جواب میشه ۱۳ .چرا؟ فرض کنید ۴ بیت داریم (۴ خانه) که هر یک ۲ مقدار می تواند داشته باشد پس ۴ ^۲= ۱۶ حالت داریم اما ۳ حالت غیر مجاز داریم( ۴ خانه سفید - ۳ خانه اول سفید - ۳ خانه آخر سفید) پس ۳-۱۶ تعداد کل حالات میشه
میتونید با رابطه بازگشتی داده شده اینو رو نشان بدین
![[تصویر: attachment.php?aid=2658]](https://manesht.ir/forum/attachment.php?aid=2658)
برای ۴ خانه در نظر بگیرید جواب میشه ۱۳ .چرا؟ فرض کنید ۴ بیت داریم (۴ خانه) که هر یک ۲ مقدار می تواند داشته باشد پس ۴ ^۲= ۱۶ حالت داریم اما ۳ حالت غیر مجاز داریم( ۴ خانه سفید - ۳ خانه اول سفید - ۳ خانه آخر سفید) پس ۳-۱۶ تعداد کل حالات میشه
میتونید با رابطه بازگشتی داده شده اینو رو نشان بدین
۰
ارسال: #۱۶
[نکات] کارآیی، تحلیل و مرتبه الگوریتمها - روابط بازگشتی
نکته در مورد قضیه اصلی:
در بعضی موارد نمی توان از قضیه اصلی استفاده کرد مانند مثال های زیر:
۱) T(n)=2T(n/2)+nlogn
T(n)=2T(n/2)+n/logn(2
زیرا در مورد ۱ علیرغم اینکه با استفاده از قضیه اصلی n=O(nlognولی چون به صورت چندجمله ای بزرگتر نیست پس نمی توان از قضیه اصلی استفاده کرد.
در مورد ۲ هم n/logn=O(n ولی حاصل تقسیم تابع بزرگتر بر کوچکتر چند جمله ای نیست پس از این قضیه نمی توان استفاده کرد .
منبع: صفحه ۹۸CLRS
در بعضی موارد نمی توان از قضیه اصلی استفاده کرد مانند مثال های زیر:
۱) T(n)=2T(n/2)+nlogn
T(n)=2T(n/2)+n/logn(2
زیرا در مورد ۱ علیرغم اینکه با استفاده از قضیه اصلی n=O(nlognولی چون به صورت چندجمله ای بزرگتر نیست پس نمی توان از قضیه اصلی استفاده کرد.
در مورد ۲ هم n/logn=O(n ولی حاصل تقسیم تابع بزرگتر بر کوچکتر چند جمله ای نیست پس از این قضیه نمی توان استفاده کرد .
منبع: صفحه ۹۸CLRS
۰
ارسال: #۱۷
[نکات] کارآیی، تحلیل و مرتبه الگوریتمها - روابط بازگشتی
(۱۴ آبان ۱۳۹۰ ۱۲:۲۶ ق.ظ)mojgan نوشته شده توسط:in quiz haye danesh gahe mit too site khode daneshgah hast berid az oonja download konid(21 آذر ۱۳۸۹ ۰۱:۵۶ ب.ظ)Masoud05 نوشته شده توسط: با سلا م به دوستان، یه فایل upload براتون کردم که سوالات دانشگاه MIT هست جواب هم کنارش هست . خیلی فوق العاده هست . حتماً حتماً حتماً دانلود کنید
مهمان عزیز شما قادر به مشاهده پیوندهای انجمن مانشت نمیباشید. جهت مشاهده پیوندها ثبت نام کنید.
سلام
مرسی از این همه همت
من نتونستم این رو دانلود کنم
دقیقا رو کدو گزینه برم
چون هر جا کلیلک می کنم یا صفحهی دیگه باز می شه یا با پسوند اچ تیام ال ذخیره می شه
ممنون
۰
ارسال: #۱۸
[نکات] کارآیی، تحلیل و مرتبه الگوریتمها - روابط بازگشتی
سلام
من یه سوال دارم؟؟؟؟؟
سوال ۸۹ ای تی:
۴f(n/2)+n^2logn
به نظر من میشه n^2logn ولی جواب زده n^2 (log〖n)〗^۲
من کتوجه نمی شم چرا مکه k همون ۲ نیست پس باید بگیم b^k=a و جواب میشه n^2logn ؟؟
ممکنه کسی کمک کنه؟؟
من یه سوال دارم؟؟؟؟؟
سوال ۸۹ ای تی:
۴f(n/2)+n^2logn
به نظر من میشه n^2logn ولی جواب زده n^2 (log〖n)〗^۲
من کتوجه نمی شم چرا مکه k همون ۲ نیست پس باید بگیم b^k=a و جواب میشه n^2logn ؟؟
ممکنه کسی کمک کنه؟؟
۰
ارسال: #۱۹
[نکات] کارآیی ، تحلیل و مرتبه الگوریتم ها - روابط بازگشتی
ارسال: #۲۰
RE: [نکات] کارآیی ، تحلیل و مرتبه الگوریتم ها - روابط بازگشتی
Can I see some ID?
Feeling left out?
نگران نباش، فقط روی این لینک برای ثبت نام کلیک کن. رمزت رو فراموش کردی؟ اینجا به یادت میاریم! close


