(۰۹ آذر ۱۳۹۵ ۱۲:۵۶ ب.ظ)kilookiloo نوشته شده توسط:  سلام . دوستان این دو معادله رو از کتاب ۶۰۰ مساله آوردم . نمیفهمم که چه فرقی توی این دوتا هست که دومین رابطه جوابش مثل اولی نمیشه ! من وقتی درختش رو رسم میکنم به این نتیجه میرسم که جواب باید دقیقا مثل اولی باشه . ممنون میشم توضیحی برای دومی ارائه بدید

---

شاید دلیلش اینه که جمع ضرایب کوچکتر از ۱ میشه پس ثابت در نظر میگیرتش

سلام.با روشهای زیادی میشه حلش کرد.
۱)درخت بازگشت

---------------------------------------------------

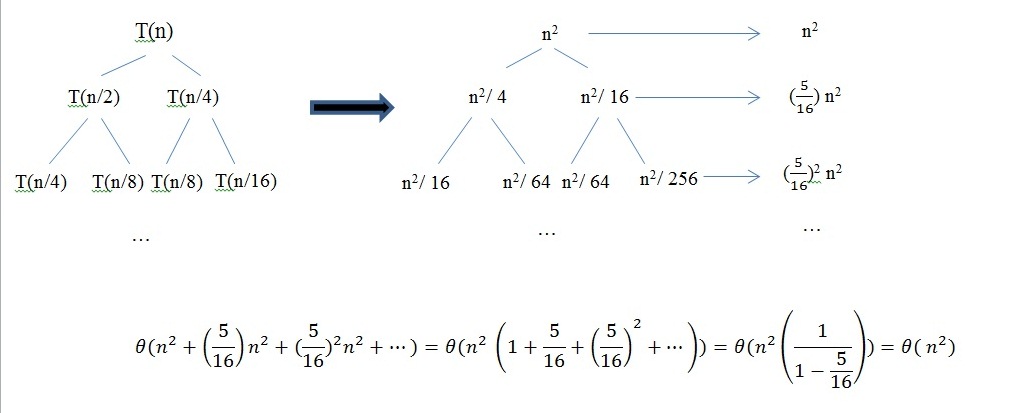
۲)قضیه Akra-Bazzi
ابتدا p رو محاسبه میکنیم:

$(2^{-p})^2\: +\: (2^{-p})\: =1\: \longrightarrow\: if\: 2^{-p}=k\: \: \longrightarrow\: \: k^2\: +\: k\: -1\: =0\: \: \longrightarrow\: \: k\: =\: \frac{-1\: \pm\: \sqrt{5}}{2}\: \: \longrightarrow\: \: 2^{-p}\: =\: \frac{-1\: \pm\: \sqrt{5}}{2}\: \: \: \longrightarrow\: \: \frac{1}{2^p}\: =\: \frac{-1\pm\sqrt{5}}{2}\: \: \longrightarrow\: 2^p\: =\frac{\: 2}{-1\pm\sqrt{5}}\: \: \longrightarrow\: p=\log^{\frac{2}{-1+\sqrt{5}}}_2\: =\: \lg2\: -\: \lg(-1+\sqrt{5})\: =\varepsilon$

سپس محاسبه فرمول زیر:
$T(n)=\: \theta(n^p(1+\int_1^n\frac{f(u)}{u^{p+1}}du))\: =\: \theta(n^p(1+\int_1^n\frac{u^2}{u^{p+1}}du))\: =\: \theta(n^p(1+\int_1^nu^{1-p}du))\: =\: \theta(n^p(1+\frac{n^{2-p}}{2-p}-\frac{1}{2-p}))\: =\: \theta(n^p(\frac{1-p+n^{2-p}}{2-p}))\: =\: \theta(\frac{n^p}{2-p}\: -\frac{pn^p}{2-p}\: +\frac{\: n^2}{2-p})\: =\: \theta(\frac{(1-p)n^p}{2-p}\: +\: \frac{n^2}{2-p})\:$

که چون P یک مقدار بین ۰ و ۱ است،پس جواب برابر است با:

$T(n)=\: \theta(n^2)$

-------------------------------------------------------------

۳- با تغییر متغیر هم میتونید جوابشو بدست بیارید.