۰
subtitle
ارسال: #۱
AVL
بچه ها شما چرخش رو متوجه میشین؟
من اصلا نمیفهمم رو چه حسابی این چرخش انجام میشه
چهارتا کتاب رو دیدم باز نفهمیدم
فقط میگن چپ راست چپ راست زربدر دایره 
اگه لطف کنبن داستانش رو بگین ممنون میشم
من اصلا نمیفهمم رو چه حسابی این چرخش انجام میشه
چهارتا کتاب رو دیدم باز نفهمیدم
فقط میگن چپ راست چپ راست زربدر دایره

اگه لطف کنبن داستانش رو بگین ممنون میشم
۶
ارسال: #۲
RE: AVL
سلام.خب من دوران رو میگم یعنی اون کاری که خودم انجام میدم!!شایدم سخت باشه ولی خب میگم حالا شاید کمک کرد
اول یکم درباره [tex]AVL[/tex] بگیم که این درخت چیه اصلا!
[tex]AVL[/tex] درخت جست وجو دودوی متوازن هستش!!!اگه یادتون باشه توی درخت [tex]BST[/tex] عملیات هایی مثل درج و جست وجو و... به ارتفاع درخت وابسته بود و حالا این احتمال وجود داشت که درخت مورب باشه و اونوقت کارمون درمیومد و باید تمام گره ها رو در بدترین حالت بررسی میکردیم
ولی اینجا این مشکل رو نداریم و همه چی لگاریتمی هستش که این کار رو به وسیله فاکتور توازن انجام میدیم!!فاکتور توازن نمیذاره ارتفاع درخت از حالت توازنش(لگاریتمی بودن) خارج شه و به این صورت تعریفش میکنیم:
خب حالا سوال اینه این فاکتور توازن چه موقع به هم میخوره؟؟؟
با یه مثال میگم!!!ببینید فرض کنید اول ما فقط نود ریشه رو داریم الان فاکتور توازن ریشه ۰ هستش!!بعدش یه نود به زیر درخت سمت چپ اضافه میکنیم فاکتور توازن ریشه ۱ میشه.دوباره یه نود به زیر درخت سمت چپ اضافه میکنیم و الان فاکتور توازن ریشه ۲ میشه!!و درختمون الان از حالت متوازن بودن خارج هستش
راه کار چیه؟؟؟اینجاست که دوران وارد میشه ما باید نود یه سری نود ها رو دوران (چرخش یا [tex]Rotate[/tex] ) بدیم تا این مشکل رو حل کنیم
این به هم ریختگی فاکتور توازن ۴ تا حالت مختلف داره که یکی یکی بررسی میکنیم
قبلش همین اول کار من میخوام ۳ تا پارامتر تعریف کنم!به خاطر سپاریشون هم اصلا کاری نداره البته تسلط هم پیدا کردید اصلا نیازی به این پارامتر ها ندارید ولی خب الان برای اینکه بشه توضیح داد من اینا رو تعریف میکنیم
[tex]x[/tex] : نودی که فاکتور توازنش به هم ریخته
[tex]y[/tex] : فرزند [tex]x[/tex]
[tex]z[/tex] : نودی جدیدی که درج کردیم و باعث بر هم ریختن توازن شده
همینا بودن!!فک نکنم خیلی سخت باشه اینا یادتون بمونه!!
حالت اول:اگه y فرزند راست x باشه , z هم به زیر درخت راست y اضافه شه (ببینید ریتم کار معلومه مثلا برای حالت دوم دقیقا برعکس اینه)
یا یه کار دیگه هم میتونید انجام بدید اینکه x رو داشته باش حالا y باید فرزند سمت راستش باشه و y رو در نظر بگیر z باید تو زیر درخت سمت راستش باشه حالا گره ای که فاکتور توازنش به هم خورده رو دوران میدیم یعنی x و اونم دوران به چپ.حالا نحوه دوران به چپ چجوریه؟
ببینید اینجوری تصور کنید که اون نود رو با دست گرفتی و داری به سمت چپ میچرخونیش!!!همین !!
اون نود و فرزنداش رو فقط میچرخونیم . به بقیه نودا کاری نداریم !!!یه کوچولو ریزه کاری داره که اونا رو فعلا نمیگم تا پیچیده نشه پس یه بار دیگه هم میگم مثل اینه که با دستت اون نود رو گرفتی رو داری با دستت به سمت چپ میچرخونی
من یه مثال زدم تا ببینی اون فلشی که تو شکل به عنوان جهت دوران نشون دادم تصور کن خودت داری اون نود رو میچرخونی
حالت دوم:اگه y فرزند چپ x باشه , z هم به زیر درخت چپ y اضافه شه یا یه کار دیگه هم میتونید انجام بدید اینکه x رو داشته باش حالا y باید فرزند سمت چپش باشه و y رو در نظر بگیر z باید تو زیر درخت سمت چپش باشه حالا گره ای که فاکتور توازنش به هم خورده رو دوران میدیم یعنی x و اونم دوران به راست.حالا نحوه دوران به راست چجوریه؟
اینجوری تصور کنید که اون نود رو با دست گرفتی و داری به سمت راست میچرخونیش!!!همین !!
فعلا این دوتا رو میگم که اگه خوشتون نیومد این همه تایپ نکرده باشم!!!

این مثال رو هم ببینید و خودتون باهاش این دوتا دوران رو انجام بدید و مثالای مشابه که یا حالت اول هستن و یا حالت دوم و اگه دیدید کار با این روش براتون راحته بگید تا دو تا حالت دیگه رو هم بگم!!
مهمان عزیز شما قادر به مشاهده پیوندهای انجمن مانشت نمیباشید. جهت مشاهده پیوندها ثبت نام کنید.
اول یکم درباره [tex]AVL[/tex] بگیم که این درخت چیه اصلا!
[tex]AVL[/tex] درخت جست وجو دودوی متوازن هستش!!!اگه یادتون باشه توی درخت [tex]BST[/tex] عملیات هایی مثل درج و جست وجو و... به ارتفاع درخت وابسته بود و حالا این احتمال وجود داشت که درخت مورب باشه و اونوقت کارمون درمیومد و باید تمام گره ها رو در بدترین حالت بررسی میکردیم
ولی اینجا این مشکل رو نداریم و همه چی لگاریتمی هستش که این کار رو به وسیله فاکتور توازن انجام میدیم!!فاکتور توازن نمیذاره ارتفاع درخت از حالت توازنش(لگاریتمی بودن) خارج شه و به این صورت تعریفش میکنیم:
ارتفاع زیر درخت سمت راستش - ارتفاع زیردرخت سمت چپش=فاکتور توازن برای نود مورد نظر ما
مقادیر مجاز هم برای فاکتور توازن [tex]-1,0,1[/tex] هستشخب حالا سوال اینه این فاکتور توازن چه موقع به هم میخوره؟؟؟
با یه مثال میگم!!!ببینید فرض کنید اول ما فقط نود ریشه رو داریم الان فاکتور توازن ریشه ۰ هستش!!بعدش یه نود به زیر درخت سمت چپ اضافه میکنیم فاکتور توازن ریشه ۱ میشه.دوباره یه نود به زیر درخت سمت چپ اضافه میکنیم و الان فاکتور توازن ریشه ۲ میشه!!و درختمون الان از حالت متوازن بودن خارج هستش
راه کار چیه؟؟؟اینجاست که دوران وارد میشه ما باید نود یه سری نود ها رو دوران (چرخش یا [tex]Rotate[/tex] ) بدیم تا این مشکل رو حل کنیم
این به هم ریختگی فاکتور توازن ۴ تا حالت مختلف داره که یکی یکی بررسی میکنیم
قبلش همین اول کار من میخوام ۳ تا پارامتر تعریف کنم!به خاطر سپاریشون هم اصلا کاری نداره البته تسلط هم پیدا کردید اصلا نیازی به این پارامتر ها ندارید ولی خب الان برای اینکه بشه توضیح داد من اینا رو تعریف میکنیم
[tex]x[/tex] : نودی که فاکتور توازنش به هم ریخته
[tex]y[/tex] : فرزند [tex]x[/tex]
[tex]z[/tex] : نودی جدیدی که درج کردیم و باعث بر هم ریختن توازن شده
همینا بودن!!فک نکنم خیلی سخت باشه اینا یادتون بمونه!!
حالت اول:اگه y فرزند راست x باشه , z هم به زیر درخت راست y اضافه شه (ببینید ریتم کار معلومه مثلا برای حالت دوم دقیقا برعکس اینه)
یا یه کار دیگه هم میتونید انجام بدید اینکه x رو داشته باش حالا y باید فرزند سمت راستش باشه و y رو در نظر بگیر z باید تو زیر درخت سمت راستش باشه حالا گره ای که فاکتور توازنش به هم خورده رو دوران میدیم یعنی x و اونم دوران به چپ.حالا نحوه دوران به چپ چجوریه؟
ببینید اینجوری تصور کنید که اون نود رو با دست گرفتی و داری به سمت چپ میچرخونیش!!!همین !!
اون نود و فرزنداش رو فقط میچرخونیم . به بقیه نودا کاری نداریم !!!یه کوچولو ریزه کاری داره که اونا رو فعلا نمیگم تا پیچیده نشه پس یه بار دیگه هم میگم مثل اینه که با دستت اون نود رو گرفتی رو داری با دستت به سمت چپ میچرخونی
من یه مثال زدم تا ببینی اون فلشی که تو شکل به عنوان جهت دوران نشون دادم تصور کن خودت داری اون نود رو میچرخونی
حالت دوم:اگه y فرزند چپ x باشه , z هم به زیر درخت چپ y اضافه شه یا یه کار دیگه هم میتونید انجام بدید اینکه x رو داشته باش حالا y باید فرزند سمت چپش باشه و y رو در نظر بگیر z باید تو زیر درخت سمت چپش باشه حالا گره ای که فاکتور توازنش به هم خورده رو دوران میدیم یعنی x و اونم دوران به راست.حالا نحوه دوران به راست چجوریه؟
اینجوری تصور کنید که اون نود رو با دست گرفتی و داری به سمت راست میچرخونیش!!!همین !!
فعلا این دوتا رو میگم که اگه خوشتون نیومد این همه تایپ نکرده باشم!!!


این مثال رو هم ببینید و خودتون باهاش این دوتا دوران رو انجام بدید و مثالای مشابه که یا حالت اول هستن و یا حالت دوم و اگه دیدید کار با این روش براتون راحته بگید تا دو تا حالت دیگه رو هم بگم!!
مهمان عزیز شما قادر به مشاهده پیوندهای انجمن مانشت نمیباشید. جهت مشاهده پیوندها ثبت نام کنید.
ارسال: #۳
RE: AVL
(۲۴ دى ۱۳۹۳ ۰۱:۲۰ ب.ظ)miladcr7 نوشته شده توسط: اگه دیدید کار با این روش براتون راحته بگید تا دو تا حالت دیگه رو هم بگم!!سلام
مهمان عزیز شما قادر به مشاهده پیوندهای انجمن مانشت نمیباشید. جهت مشاهده پیوندها ثبت نام کنید.
نلطفا اون دو حالت دیگه رو هم بهمون بگید؟؟؟؟؟؟
ممنون به خاطر وقتی که میذارید.
۲
ارسال: #۴
RE: AVL
دوست عزیز اگه بخوای چرخش رو عین نوشته های کتاب متوجه بشی کلاً ساختمون داده یادت میره . 
مثلاً نوشته تو چرخش راست راست : زیر درخت راست گره جایگزین در صورت وجود میشه زیر درخت چپ محور





حالا بماند چرخش مضاعف چی میشه که آدم سرگیجه میگیره

من ترفند یاد گرفتن خودمد میگم شاید تاثیری داشت براتون
ببین من یک مثال رو براتون ضمیمه کردم . اگه تو این مثال ببینین گرهی که درج کردیم (۱۲) درخت ما رو نامتوازن کرده . حالا این عدم توازن کجا به چشم میخوره . تو گره ( ۹) . چون ارتفاع توازنش -۲ هستش و بیشتر از ۱ اختلاف داره .
حالا شما فرض کن یه زنجیر دستته که ارتفاع یه ورش خیلی بیشتر از طرغ دیگشه . پس تو باید کمبود ارتفاع رو جبران کنی دیگه ( از اینور ارتفاع رو کم کنی و از طرف دیگش ارتفاعشو زیاد منی ) .
پس گره محور رو در جهت مخالف ۱۲ میچرخونی که ارتفاع ۱۲ رو کم کنی تا توازن رو بتونی درست کنی
حالا زنجیر رو در جهت ارتفاع کم بیاری پایین فرزند چپ ۹ میاد جای ۹ . چرا ؟ چون داری ارتفاع زیر درخت راست ۹ رو یکی یکی کم میکنی که ۱۲ ارتفاعش کم شه و توازن بر هم نخوره .
۱۳ هم میاد بالا یکی . ۱۲ هم یکی میاد بالا
حالا ما یه گره ۱۰ داریم که اونو نیاوردیم بالا . درسته ؟؟
حالا تکلیف جیه ؟
برادر من تکلیف الهیه !
ببین زنجیر رو که میکشی بالا . اونایی که وصلن به زنجیر یکی یکی میان بالا دیگه
ولی ۱۰ ( شیوه من ) چون فرزند ناخلف ۱۱ هستش یکی بالا کشیدنش نامعقوله .
پس این گره میره فرزند گره مجور میشه . گره محورمونم که ۹ بود .
راست راست هم شبیه اینه .
منتهی زنجیر رو از طرف دیگه میکشیم بالا
حالا تو پست بعدی مضاعف رو میگم
فقط تو باید بدونی که ما در کل میخوایم گره جدید رو که ارتفاع رو برهم زده بکشیم بالا که توازن حفظ بشه . حالا زنجیر رو باید در جهت مخالف بیاری پایین که از اون طرف بالا بیاد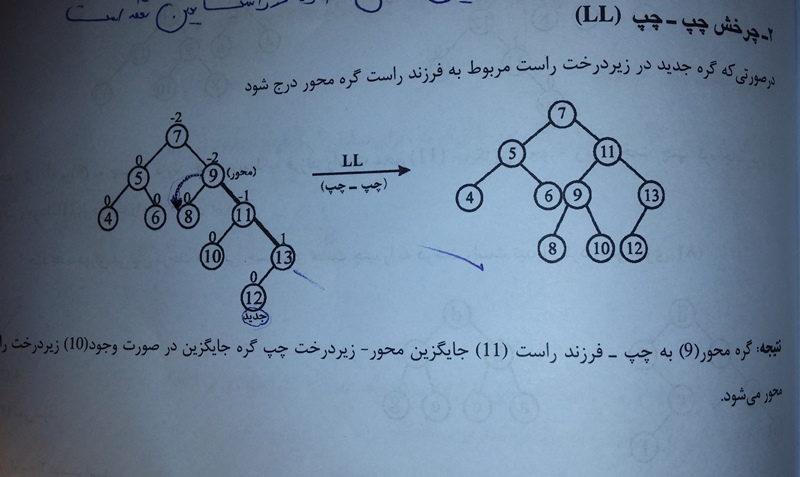
حالا چرخش مضاعف
ببین گرهی که تو شکل ضمیمه بهعنوان گره جدیده ۱۰ هستش
این گره نه تو چپ ترین گره درج شده . نه تو راست ترین .
پس یه چرحش مضاعف داره
( دقت کن که درج تو AVL چون درختمون جستجوی دودویی متوازن هست پس عین درج BST هستش )
حالا گره ( ۹) عدم توازن رو نشون داده و گره محوورمون میشه
حالا زنجیرمون از طرف راست بلنده . از طرف چپ کوتاه
پس یکم باید از طرف راست کوتاهش کنیم .
با انبردست حق نداریم ببریمش !!
پس ارتفاع جهت مخالفشو زیاد میکنیم
حالا این چرخشمون مضاعفه
دیگه اینجا ۱۲ جایگزین ۹ نمیشه . چرخش مضاعفه
بلکه اونی که جایگزین میشه پدر گره جدید هستش
یعنی ۱۱ جایگزین گره ۹ میشه
حالا ۱۰ اینجا ول معطل موند . تکلیف چیه ؟
 نه الهی نیست
نه الهی نیست
گره محور میاد اونو به عنوان فرزند خوندگی ! قبول میکنه . میشه فرزند گره محور

مثلاً نوشته تو چرخش راست راست : زیر درخت راست گره جایگزین در صورت وجود میشه زیر درخت چپ محور





حالا بماند چرخش مضاعف چی میشه که آدم سرگیجه میگیره

من ترفند یاد گرفتن خودمد میگم شاید تاثیری داشت براتون
ببین من یک مثال رو براتون ضمیمه کردم . اگه تو این مثال ببینین گرهی که درج کردیم (۱۲) درخت ما رو نامتوازن کرده . حالا این عدم توازن کجا به چشم میخوره . تو گره ( ۹) . چون ارتفاع توازنش -۲ هستش و بیشتر از ۱ اختلاف داره .
حالا شما فرض کن یه زنجیر دستته که ارتفاع یه ورش خیلی بیشتر از طرغ دیگشه . پس تو باید کمبود ارتفاع رو جبران کنی دیگه ( از اینور ارتفاع رو کم کنی و از طرف دیگش ارتفاعشو زیاد منی ) .
پس گره محور رو در جهت مخالف ۱۲ میچرخونی که ارتفاع ۱۲ رو کم کنی تا توازن رو بتونی درست کنی
حالا زنجیر رو در جهت ارتفاع کم بیاری پایین فرزند چپ ۹ میاد جای ۹ . چرا ؟ چون داری ارتفاع زیر درخت راست ۹ رو یکی یکی کم میکنی که ۱۲ ارتفاعش کم شه و توازن بر هم نخوره .
۱۳ هم میاد بالا یکی . ۱۲ هم یکی میاد بالا
حالا ما یه گره ۱۰ داریم که اونو نیاوردیم بالا . درسته ؟؟
حالا تکلیف جیه ؟
برادر من تکلیف الهیه !

ببین زنجیر رو که میکشی بالا . اونایی که وصلن به زنجیر یکی یکی میان بالا دیگه
ولی ۱۰ ( شیوه من ) چون فرزند ناخلف ۱۱ هستش یکی بالا کشیدنش نامعقوله .
پس این گره میره فرزند گره مجور میشه . گره محورمونم که ۹ بود .
راست راست هم شبیه اینه .
منتهی زنجیر رو از طرف دیگه میکشیم بالا
حالا تو پست بعدی مضاعف رو میگم
فقط تو باید بدونی که ما در کل میخوایم گره جدید رو که ارتفاع رو برهم زده بکشیم بالا که توازن حفظ بشه . حالا زنجیر رو باید در جهت مخالف بیاری پایین که از اون طرف بالا بیاد

حالا چرخش مضاعف
ببین گرهی که تو شکل ضمیمه بهعنوان گره جدیده ۱۰ هستش
این گره نه تو چپ ترین گره درج شده . نه تو راست ترین .
پس یه چرحش مضاعف داره
( دقت کن که درج تو AVL چون درختمون جستجوی دودویی متوازن هست پس عین درج BST هستش )
حالا گره ( ۹) عدم توازن رو نشون داده و گره محوورمون میشه
حالا زنجیرمون از طرف راست بلنده . از طرف چپ کوتاه
پس یکم باید از طرف راست کوتاهش کنیم .
با انبردست حق نداریم ببریمش !!
پس ارتفاع جهت مخالفشو زیاد میکنیم
حالا این چرخشمون مضاعفه
دیگه اینجا ۱۲ جایگزین ۹ نمیشه . چرخش مضاعفه
بلکه اونی که جایگزین میشه پدر گره جدید هستش
یعنی ۱۱ جایگزین گره ۹ میشه
حالا ۱۰ اینجا ول معطل موند . تکلیف چیه ؟
 نه الهی نیست
نه الهی نیست گره محور میاد اونو به عنوان فرزند خوندگی ! قبول میکنه . میشه فرزند گره محور

۱
۰
ارسال: #۷
RE: AVL
سلام 
از روی کتاب ساختمان پوران بخونید راحت گفته ( چون باید شکل ها شو ببنید و تصور کنید که وقتی بچرخه چی میشه). کلا بحث چرجش چند تا حالت داره:
۱) اگه درخت مورب به راست باشه باید ریشه رو به سمت چپ بخرخونیم تا متوازن بشه
۲) اگه درخت مورب به چپ باشه باید ریشه درخت را به سمت راست بچرخونیم.
( توی این دو حالت ریشه درخت در جهت عکس مورب بودنش میچرخه یعنی اگه مورب به راسته ریشه باید به سمت چپ بچرخه و برعکس)
۳)حالتی که درخت مورب نیست یعنی مثلا سطح اول که ریشه هست و در سطح دوم گره در سمت چپ ریشه قرار داره و در سطح سوم گره در سمت راست گره قبلی هستش و یا برعکس . توی این شرایط اول باید درخت به صورت مورب در بیاد تا مثل حالت یک یا دو مورب به راست یا چپ بشه بعد دوباره یه دوران دیگه داده بشه تا متوازن بشه.

از روی کتاب ساختمان پوران بخونید راحت گفته ( چون باید شکل ها شو ببنید و تصور کنید که وقتی بچرخه چی میشه). کلا بحث چرجش چند تا حالت داره:
۱) اگه درخت مورب به راست باشه باید ریشه رو به سمت چپ بخرخونیم تا متوازن بشه
۲) اگه درخت مورب به چپ باشه باید ریشه درخت را به سمت راست بچرخونیم.
( توی این دو حالت ریشه درخت در جهت عکس مورب بودنش میچرخه یعنی اگه مورب به راسته ریشه باید به سمت چپ بچرخه و برعکس)
۳)حالتی که درخت مورب نیست یعنی مثلا سطح اول که ریشه هست و در سطح دوم گره در سمت چپ ریشه قرار داره و در سطح سوم گره در سمت راست گره قبلی هستش و یا برعکس . توی این شرایط اول باید درخت به صورت مورب در بیاد تا مثل حالت یک یا دو مورب به راست یا چپ بشه بعد دوباره یه دوران دیگه داده بشه تا متوازن بشه.
۰
ارسال: #۹
RE: AVL
۰
ارسال: #۱۰
RE: AVL
سلام.چشششم حتما همون کاری رو که خودم انجام میدم به شما هم میگم!!سختی و اسونیش بمونه دیگه
۰
۰
موضوعهای مرتبط با این موضوع... |
|||||
| موضوع: | نویسنده | پاسخ: | بازدید: | آخرین ارسال | |
| چرخش در AVL | MiladCr7 | ۱ | ۱,۸۸۶ |
۰۷ بهمن ۱۳۹۳ ۱۲:۳۱ ب.ظ آخرین ارسال: kefsan |
|
| سوال از AVL | tm.viper | ۳ | ۲,۵۸۷ |
۰۶ بهمن ۱۳۹۳ ۱۰:۰۶ ق.ظ آخرین ارسال: tm.viper |
|
| مشکل در حل سوالات درخت AVL؟؟؟ | mostafa2012 | ۱ | ۱,۹۹۳ |
۰۲ بهمن ۱۳۹۳ ۱۲:۰۵ ق.ظ آخرین ارسال: shayesteb |
|
| درج و حذف AVL | teacherpc | ۲۱ | ۲۰,۹۸۷ |
۰۹ دى ۱۳۹۳ ۱۱:۱۸ ب.ظ آخرین ارسال: setarehfb |
|
| AVL - اختلاف سطح | Ametrine | ۲ | ۲,۶۷۵ |
۰۴ آبان ۱۳۹۳ ۰۶:۰۳ ب.ظ آخرین ارسال: Ametrine |
|
| تبدیل bst به AVL | abji22 | ۶ | ۴,۴۴۱ |
۰۸ بهمن ۱۳۹۲ ۱۱:۰۱ ب.ظ آخرین ارسال: abji22 |
|
| ساختمان داده، درخت AVL, کامپیوتر ۸۵ | hoomanab | ۰ | ۲,۰۶۲ |
۰۷ بهمن ۱۳۹۲ ۱۱:۰۴ ق.ظ آخرین ارسال: hoomanab |
|
| چرخش در AVL | ماهسان لیما | ۳ | ۲,۷۹۶ |
۲۰ دى ۱۳۹۲ ۰۱:۰۰ ق.ظ آخرین ارسال: ماهسان لیما |
|
| علت نامگذاری LL-RL-LR-RRدر AVL | mary1234 | ۳ | ۳,۸۵۲ |
۱۵ آذر ۱۳۹۲ ۰۱:۰۸ ق.ظ آخرین ارسال: calm boy |
|
| توضیحی با شکل درباره چرخش دادن در AVL(ساختمان داده) | tarane1992 | ۸ | ۶,۷۶۰ |
۰۶ آذر ۱۳۹۲ ۰۲:۰۷ ب.ظ آخرین ارسال: Mehrdad7soft |
|
Can I see some ID?
Feeling left out?
نگران نباش، فقط روی این لینک برای ثبت نام کلیک کن. رمزت رو فراموش کردی؟ اینجا به یادت میاریم! close



 (به روش بدون فرمول و ترجیحا با ترفند)
(به روش بدون فرمول و ترجیحا با ترفند)
