۰
subtitle
ارسال: #۱
مرتبه زمانی - آی تی ۸۸
سوال رو پیوست کردم، جواب گزینه ۳ هست،چرا؟
پوران گفته که دو تا حلقه داخلی مرتبهشون میشه n، چرا؟
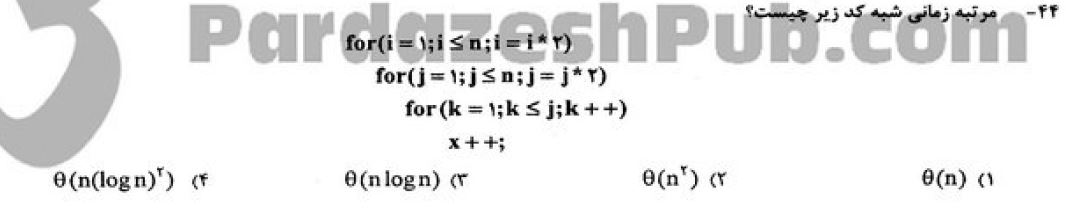
پوران گفته که دو تا حلقه داخلی مرتبهشون میشه n، چرا؟
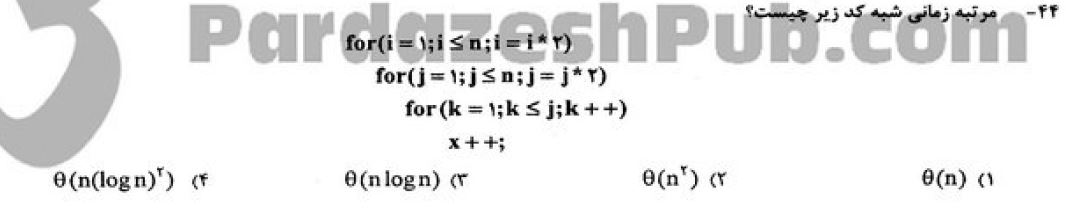
۴
ارسال: #۲
RE: مرتبه زمانی - آی تی ۸۸
ببین زمان اجرای حلقه دوم و سوم [tex]\lg(n)[/tex] نمیشه چون به ازای هر [tex]j[/tex] توی حلقه دوم مقدار [tex]k[/tex] توی حلقه سوم فرق داره درسته؟
یعنی وقتی [tex]j[/tex] مقدارش ۱ باشه حلقه سوم ۱ بار اجرا میشه و وقتی [tex]j=2[/tex] باشه حلقه سوم ۲ بار اجرا میشه و وقتی [tex]j=4[/tex] باشه حلقه سوم ۴ بار اجرا میشه پس لگاریتمی تغییر نمیکنه.
حالا این تریس رو داشته باش:
[tex]j=1\longrightarrow1[/tex]
[tex]j=2\longrightarrow2[/tex]
[tex]j=4\longrightarrow4[/tex]
[tex]j=8\longrightarrow8[/tex]
و همینطوری ادامه بده.حال قبول داری [tex]j[/tex] داره به صورت [tex]2^p[/tex] تغییر میکنه.p از صفر شروع میشه.حالا این اجرا تا چه وقتی
ادامه پیدا میکنه؟
تا وقتی که [tex]2^p<n[/tex] درسته؟یعنی وقتی که [tex]2^{p 1}>n[/tex] دیگه حلقه اجرا نمیشه.درسته؟
پس ما میتونیم یه تقریب بزنیم به این صورت که:[tex]2^{p}\cong n[/tex] درست؟
حالا مجموع زمان اجراها رو محاسبه میکنیم:
[tex]2^0 2^1 2^2 2^3 ... 2^p=\frac{2^{p 1}-1}{2-1}=2^{p 1}-1\cong n=\theta(n)[/tex]
حلقه اول هم که [tex]\lg(n)[/tex] پس زمان اجرای کل:[tex]n.\lg(n)[/tex]
یعنی وقتی [tex]j[/tex] مقدارش ۱ باشه حلقه سوم ۱ بار اجرا میشه و وقتی [tex]j=2[/tex] باشه حلقه سوم ۲ بار اجرا میشه و وقتی [tex]j=4[/tex] باشه حلقه سوم ۴ بار اجرا میشه پس لگاریتمی تغییر نمیکنه.
حالا این تریس رو داشته باش:
[tex]j=1\longrightarrow1[/tex]
[tex]j=2\longrightarrow2[/tex]
[tex]j=4\longrightarrow4[/tex]
[tex]j=8\longrightarrow8[/tex]
و همینطوری ادامه بده.حال قبول داری [tex]j[/tex] داره به صورت [tex]2^p[/tex] تغییر میکنه.p از صفر شروع میشه.حالا این اجرا تا چه وقتی
ادامه پیدا میکنه؟
تا وقتی که [tex]2^p<n[/tex] درسته؟یعنی وقتی که [tex]2^{p 1}>n[/tex] دیگه حلقه اجرا نمیشه.درسته؟
پس ما میتونیم یه تقریب بزنیم به این صورت که:[tex]2^{p}\cong n[/tex] درست؟
حالا مجموع زمان اجراها رو محاسبه میکنیم:
[tex]2^0 2^1 2^2 2^3 ... 2^p=\frac{2^{p 1}-1}{2-1}=2^{p 1}-1\cong n=\theta(n)[/tex]
حلقه اول هم که [tex]\lg(n)[/tex] پس زمان اجرای کل:[tex]n.\lg(n)[/tex]
ارسال: #۳
RE: مرتبه زمانی - آی تی ۸۸
(۲۲ مهر ۱۳۹۳ ۱۱:۲۴ ب.ظ)miladcr7 نوشته شده توسط: ببین زمان اجرای حلقه دوم و سوم [tex]\lg(n)[/tex] نمیشه چون به ازای هر [tex]j[/tex] توی حلقه دوم مقدار [tex]k[/tex] توی حلقه سوم فرق داره درسته؟ممنون، شما این تحلیل رو توی کتاب تستی، جایی دیدید؟ یا از کسی پرسیدید؟
یعنی وقتی [tex]j[/tex] مقدارش ۱ باشه حلقه سوم ۱ بار اجرا میشه و وقتی [tex]j=2[/tex] باشه حلقه سوم ۲ بار اجرا میشه و وقتی [tex]j=4[/tex] باشه حلقه سوم ۴ بار اجرا میشه پس لگاریتمی تغییر نمیکنه.
حالا این تریس رو داشته باش:
[tex]j=1\longrightarrow1[/tex]
[tex]j=2\longrightarrow2[/tex]
[tex]j=4\longrightarrow4[/tex]
[tex]j=8\longrightarrow8[/tex]
و همینطوری ادامه بده.حال قبول داری [tex]j[/tex] داره به صورت [tex]2^p[/tex] تغییر میکنه.p از صفر شروع میشه.حالا این اجرا تا چه وقتی
ادامه پیدا میکنه؟
تا وقتی که [tex]2^p<n[/tex] درسته؟یعنی وقتی که [tex]2^{p 1}>n[/tex] دیگه حلقه اجرا نمیشه.درسته؟
پس ما میتونیم یه تقریب بزنیم به این صورت که:[tex]2^{p}\cong n[/tex] درست؟
حالا مجموع زمان اجراها رو محاسبه میکنیم:
[tex]2^0 2^1 2^2 2^3 ... 2^p=\frac{2^{p 1}-1}{2-1}=2^{p 1}-1\cong n=\theta(n)[/tex]
حلقه اول هم که [tex]\lg(n)[/tex] پس زمان اجرای کل:[tex]n.\lg(n)[/tex]
آخه من تو دو، سه تا کتاب نگاه کردم همه یه خط نوشته بودن فقط.

ارسال: #۴
RE: مرتبه زمانی - آی تی ۸۸
(۲۳ مهر ۱۳۹۳ ۰۴:۰۶ ب.ظ)Ametrine نوشته شده توسط:اگه قسمتی مثل اون دو به توان p منظورتونه که اونه مشابهش توی جزوه ی استاد یوسفی هم هستش ولی اگه کل سوال رو میگید نه تحلیل خودمه(22 مهر ۱۳۹۳ ۱۱:۲۴ ب.ظ)miladcr7 نوشته شده توسط: ببین زمان اجرای حلقه دوم و سوم [tex]\lg(n)[/tex] نمیشه چون به ازای هر [tex]j[/tex] توی حلقه دوم مقدار [tex]k[/tex] توی حلقه سوم فرق داره درسته؟ممنون، شما این تحلیل رو توی کتاب تستی، جایی دیدید؟ یا از کسی پرسیدید؟
یعنی وقتی [tex]j[/tex] مقدارش ۱ باشه حلقه سوم ۱ بار اجرا میشه و وقتی [tex]j=2[/tex] باشه حلقه سوم ۲ بار اجرا میشه و وقتی [tex]j=4[/tex] باشه حلقه سوم ۴ بار اجرا میشه پس لگاریتمی تغییر نمیکنه.
حالا این تریس رو داشته باش:
[tex]j=1\longrightarrow1[/tex]
[tex]j=2\longrightarrow2[/tex]
[tex]j=4\longrightarrow4[/tex]
[tex]j=8\longrightarrow8[/tex]
و همینطوری ادامه بده.حال قبول داری [tex]j[/tex] داره به صورت [tex]2^p[/tex] تغییر میکنه.p از صفر شروع میشه.حالا این اجرا تا چه وقتی
ادامه پیدا میکنه؟
تا وقتی که [tex]2^p<n[/tex] درسته؟یعنی وقتی که [tex]2^{p 1}>n[/tex] دیگه حلقه اجرا نمیشه.درسته؟
پس ما میتونیم یه تقریب بزنیم به این صورت که:[tex]2^{p}\cong n[/tex] درست؟
حالا مجموع زمان اجراها رو محاسبه میکنیم:
[tex]2^0 2^1 2^2 2^3 ... 2^p=\frac{2^{p 1}-1}{2-1}=2^{p 1}-1\cong n=\theta(n)[/tex]
حلقه اول هم که [tex]\lg(n)[/tex] پس زمان اجرای کل:[tex]n.\lg(n)[/tex]
آخه من تو دو، سه تا کتاب نگاه کردم همه یه خط نوشته بودن فقط.
۰
ارسال: #۵
Re: مرتبه زمانی - آی تی ۸۸
دوحلقه داخلی بهم وابسته اند. در ۱=j حلقه داخلی تر یکبار اجرا میشه. در ۲=j دستور دوبار اجرا میشه و در ۴=j هم که ۴ بار دستور اجرا میشه و الی آخر. فرض میکنیم n توانی از دو باشه و مثلا دو به توان k باشه.
۱+۲+۴+...+(۲^k) =( 2^k+1) - 1 = 2*(2^k) - 1 =2n-1
حلقه اول هم که چون هردفعه به توان دو میرسه logn میشه.درنتیجه میشه nlogn
Sent from my GT-S5660 using Tapatalk 2
۱+۲+۴+...+(۲^k) =( 2^k+1) - 1 = 2*(2^k) - 1 =2n-1
حلقه اول هم که چون هردفعه به توان دو میرسه logn میشه.درنتیجه میشه nlogn
Sent from my GT-S5660 using Tapatalk 2
موضوعهای مرتبط با این موضوع... |
|||||
| موضوع: | نویسنده | پاسخ: | بازدید: | آخرین ارسال | |
| سلام لطفاً یکی به من بگه مرتبه زمانی ها چطوری به log تبدیل میشن فرمول داره؟؟ | Azadam | ۶ | ۷,۳۹۸ |
۰۶ دى ۱۴۰۰ ۰۹:۰۲ ق.ظ آخرین ارسال: Soldier's life |
|
| مرتبه ایجاد درخت | rad.bahar | ۱ | ۴,۲۷۸ |
۳۰ مهر ۱۳۹۹ ۰۳:۳۴ ب.ظ آخرین ارسال: rad.bahar |
|
| مرتبه شبه کد | rad.bahar | ۱ | ۳,۰۷۳ |
۲۲ مهر ۱۳۹۹ ۰۹:۳۲ ب.ظ آخرین ارسال: BBumir |
|
| حل مساله مرتبه زمانی حلقه های تو در تو | sarashahi | ۱۶ | ۲۷,۳۹۹ |
۱۹ خرداد ۱۳۹۹ ۰۱:۱۶ ب.ظ آخرین ارسال: gillda |
|
| مرتبه زمانی | Sanazzz | ۱۷ | ۲۶,۵۶۱ |
۰۹ اردیبهشت ۱۳۹۹ ۰۶:۴۶ ب.ظ آخرین ارسال: mohsentafresh |
|
| پیچیدگی زمانی اکشن های قابل اعمال در یک وضعیت | اsepid8994 | ۰ | ۲,۴۵۱ |
۲۹ اسفند ۱۳۹۸ ۱۲:۵۱ ب.ظ آخرین ارسال: اsepid8994 |
|
| مرتبه زمانی یافتن قطر | Sepideh96 | ۲ | ۴,۷۸۳ |
۰۸ آذر ۱۳۹۸ ۰۴:۳۴ ب.ظ آخرین ارسال: erfan30 |
|
| مرتبه مانی | Sanazzz | ۳ | ۴,۹۰۷ |
۰۵ خرداد ۱۳۹۸ ۰۲:۳۶ ب.ظ آخرین ارسال: Sanazzz |
|
| یافتن دو عدد پیچیدگی زمانی O(n) | porseshgar | ۲ | ۵,۰۷۷ |
۱۵ بهمن ۱۳۹۷ ۱۲:۱۶ ب.ظ آخرین ارسال: porseshgar |
|
| مرتبه زمانی | Sanazzz | ۰ | ۲,۵۳۷ |
۰۴ بهمن ۱۳۹۷ ۰۵:۴۱ ب.ظ آخرین ارسال: Sanazzz |
|
Can I see some ID?
Feeling left out?
نگران نباش، فقط روی این لینک برای ثبت نام کلیک کن. رمزت رو فراموش کردی؟ اینجا به یادت میاریم! close


