۱
subtitle
ارسال: #۱
رابطه بازگشتی برای دنباله های n رقمی باشرط؟
سلام.رابطه بازگشتی برای تعداد دنباله های n رقمی از ارقام ۰و ۱و۲و۳ که شامل دنباله های ۲۱و۱۲و۱۱ نباشد؟
لطفا راه حل رو هم توضیح بدین .ممنون
لطفا راه حل رو هم توضیح بدین .ممنون
۳
ارسال: #۲
RE: رابطه بازگشتی برای دنباله های n رقمی باشرط؟
سلام. این سوال مشابه سوال کنکور سال ۹۱ بوده.
فرض کنید an تعداد رشته های صحیح بطول n باشه که به ارقام ۰ تا ۳ ختم میشن. اگه رقم سمت راست ۰ یا ۳ باشه پشت سرش یه دنباله بطول n-1 میتونه بیاد که این زیررشته هارو نداره. (یعنی همون جمله n-1ام دنباله) ولی اگه رقم سمت راست قراره ۱ باشه باید قبل از ۱ یک رقم ۰ یا ۳ داشته باشیم. قبل از اون ۰ و ۳ هم میتونه یه دنباله صحیح بطول n-2 بیاد. اگه رقم سمت راست ۲ باشه علاوه بر حالتی که برای رقم یکان ۱ داشتیم، میتونیم یه تعداد ۲ داشته باشیم و بعدش ۰ یا ۳ داشته باشیم. این رابطه با P نشون داده شده. اون ۱ آخر هم برای اینه که میشه تمام ارقام از ۲ تشکیل بشن. رابطه بصورت زیر نوشته میشه:
ساده شدش میشه: (با محاسبه تفاضل ۲ جمله پشت سر هم میشه به این عبارت رسید.)
فرض کنید an تعداد رشته های صحیح بطول n باشه که به ارقام ۰ تا ۳ ختم میشن. اگه رقم سمت راست ۰ یا ۳ باشه پشت سرش یه دنباله بطول n-1 میتونه بیاد که این زیررشته هارو نداره. (یعنی همون جمله n-1ام دنباله) ولی اگه رقم سمت راست قراره ۱ باشه باید قبل از ۱ یک رقم ۰ یا ۳ داشته باشیم. قبل از اون ۰ و ۳ هم میتونه یه دنباله صحیح بطول n-2 بیاد. اگه رقم سمت راست ۲ باشه علاوه بر حالتی که برای رقم یکان ۱ داشتیم، میتونیم یه تعداد ۲ داشته باشیم و بعدش ۰ یا ۳ داشته باشیم. این رابطه با P نشون داده شده. اون ۱ آخر هم برای اینه که میشه تمام ارقام از ۲ تشکیل بشن. رابطه بصورت زیر نوشته میشه:
[tex]a_n=2a_{n-1} 4a_{n-2} p_{n-2} 1[/tex]
[tex]a_0=1[/tex]
[tex]a_1=4[/tex]
[tex]p_n=\sum_{i=0}^{n-1}2a_i[/tex]
[tex]a_0=1[/tex]
[tex]a_1=4[/tex]
[tex]p_n=\sum_{i=0}^{n-1}2a_i[/tex]
ساده شدش میشه: (با محاسبه تفاضل ۲ جمله پشت سر هم میشه به این عبارت رسید.)
[tex]a_n=3a_{n-1} 2a_{n-2}-2a_{n-3}[/tex]
[tex]a_0=1[/tex]
[tex]a_1=4[/tex]
[tex]a_2=13[/tex]
[tex]a_0=1[/tex]
[tex]a_1=4[/tex]
[tex]a_2=13[/tex]
ارسال: #۳
RE: رابطه بازگشتی برای دنباله های n رقمی باشرط؟
(۲۲ مهر ۱۳۹۳ ۱۲:۰۶ ق.ظ)Jooybari نوشته شده توسط: سلام. این سوال مشابه سوال کنکور سال ۹۱ بوده.
...
روش درست همینه، فقط ۲ تا اشتباه تایپی داره و [tex]a_n=2a_{n-1} 5a_{n-2}[/tex] نمیتونه درست باشه(با [tex]a_3=45[/tex] تست کنید).
اشتباهات تایپی این پاسخ هم یکی مربوط میشه به [tex]p_n[/tex] که در سیگما i باید از ۰ شروع بشه تا بتونه برای مثال [tex]2a_0[/tex] رو برای [tex]a_3[/tex] تولید کنه:
[tex]p_n=\sum_{i=0}^{n-1}2a_i[/tex]
و دومی مربوط میشه به تفاضل ۲ جمله پشت سر هم که میشه :
[tex]a_n=3a_{n-1} 2a_{n-2}-2a_{n-3}[/tex]
ارسال: #۴
RE: رابطه بازگشتی برای دنباله های n رقمی باشرط؟
(۰۸ آبان ۱۳۹۳ ۰۶:۲۳ ب.ظ)y.s نوشته شده توسط:(22 مهر ۱۳۹۳ ۱۲:۰۶ ق.ظ)Jooybari نوشته شده توسط: سلام. این سوال مشابه سوال کنکور سال ۹۱ بوده.
...
روش درست همینه، فقط ۲ تا اشتباه تایپی داره و [tex]a_n=2a_{n-1} 5a_{n-2}[/tex] نمیتونه درست باشه(با [tex]a_3=45[/tex] تست کنید).
اشتباهات تایپی این پاسخ هم یکی مربوط میشه به [tex]p_n[/tex] که در سیگما i باید از ۰ شروع بشه تا بتونه برای مثال [tex]2a_0[/tex] رو برای [tex]a_3[/tex] تولید کنه:
[tex]p_n=\sum_{i=0}^{n-1}2a_i[/tex]و دومی مربوط میشه به تفاضل ۲ جمله پشت سر هم که میشه :
[tex]a_n=3a_{n-1} 2a_{n-2}-2a_{n-3}[/tex]
سلام. متشکر. مقدار تفاضل رو درست کردم. در محاسبه اختلاف pها ضریب ۲ رو لحاظ نکرده بودم. ولی اشکالی که در p بود رو متوجه نمیشم. دنباله p باری تعداد ۲ های پشت سر همه. این تکرار ۲ مشکلی نداره ولی بعدش نباید ۱ بیاد. عدد ۱ در جمله اول هم برای اینه که این رقم میتونه تا رقم یکان تکرار بشه و لزومی نداره بعدش حتماً ۰ و ۳ بیاد.
ارسال: #۵
RE: رابطه بازگشتی برای دنباله های n رقمی باشرط؟
(۰۹ آبان ۱۳۹۳ ۰۳:۴۱ ب.ظ)Jooybari نوشته شده توسط:(08 آبان ۱۳۹۳ ۰۶:۲۳ ب.ظ)y.s نوشته شده توسط:(22 مهر ۱۳۹۳ ۱۲:۰۶ ق.ظ)Jooybari نوشته شده توسط: سلام. این سوال مشابه سوال کنکور سال ۹۱ بوده.
...
روش درست همینه، فقط ۲ تا اشتباه تایپی داره و [tex]a_n=2a_{n-1} 5a_{n-2}[/tex] نمیتونه درست باشه(با [tex]a_3=45[/tex] تست کنید).
اشتباهات تایپی این پاسخ هم یکی مربوط میشه به [tex]p_n[/tex] که در سیگما i باید از ۰ شروع بشه تا بتونه برای مثال [tex]2a_0[/tex] رو برای [tex]a_3[/tex] تولید کنه:
[tex]p_n=\sum_{i=0}^{n-1}2a_i[/tex]و دومی مربوط میشه به تفاضل ۲ جمله پشت سر هم که میشه :
[tex]a_n=3a_{n-1} 2a_{n-2}-2a_{n-3}[/tex]
سلام. متشکر. مقدار تفاضل رو درست کردم. در محاسبه اختلاف pها ضریب ۲ رو لحاظ نکرده بودم. ولی اشکالی که در p بود رو متوجه نمیشم. دنباله p باری تعداد ۲ های پشت سر همه. این تکرار ۲ مشکلی نداره ولی بعدش نباید ۱ بیاد. عدد ۱ در جمله اول هم برای اینه که این رقم میتونه تا رقم یکان تکرار بشه و لزومی نداره بعدش حتماً ۰ و ۳ بیاد.
سلام
هر رشته به طول n یک حالت داره که همه ۲ باشن که لحاظ شده، ۲ حالت هم داره که n-1 رقم سمت راست ۲ باشه و n امین رقم ۰ یا ۳ باشه که [tex]p_n[/tex] نمیتونه این ۲ حالت رو تولید کنه، یا باید به جای اضافه کردن یک واحد ۳ واحد به رابطه اضافه کنیم و یا چون [tex]a_0=1[/tex] باید مقدار [tex]2a_0[/tex] رو به رابطه اضافه کنیم، برای مثال در [tex]a_3[/tex] داریم:
برای حالتی که رقم سمت راست ۰ یا ۳ باشد داریم : [tex]2a_2[/tex]
برای حالتی که رقم سمت راست ۱ باشد داریم : [tex]2a_1[/tex]
برای حالتی که رقم سمت راست ۲ باشد و رقم دوم ۰ یا ۳ باشد داریم : [tex]2a_1[/tex]
برای حالتی که دو رقم سمت راست ۲ باشند و رقم سوم(آخر) ۰ یا ۳ باشد ۲ حالت داریم یا : [tex]2a_0[/tex]
و در آخر برای حالتی که همه ۲ هستند ۱ حالت داریم و در مجموع:
[tex]a_3=2a_2 4a_1 2a_0 1[/tex]
[tex]a_3=45[/tex]
اگر با رابطه ای که شما نوشتید جلو بریم برای [tex]a_3[/tex] خواهیم داشت:[tex]a_3=45[/tex]
[tex]a_3=2a_2 4a_1 p_1 1[/tex]
[tex]p_1=0[/tex] خواهد بود و خواهیم داشت:
[tex]a_3=2a_2 4a_1 1[/tex]
[tex]a_3=43[/tex]
ولی اگه در [tex]p_n[/tex] ، سیگما از i=0 شروع بشه [tex]p_1=2a_0[/tex] خواهد شد و برای تمام n ها هم اون ۲ حالتی که n-1 رقم ۲ هست و رقم آخر ۰ یا ۳ هست رو لحاظ میکنه
[tex]a_3=43[/tex]
ارسال: #۶
RE: رابطه بازگشتی برای دنباله های n رقمی باشرط؟
(۰۹ آبان ۱۳۹۳ ۰۸:۴۶ ب.ظ)y.s نوشته شده توسط: اگر با رابطه ای که شما نوشتید جلو بریم برای [tex]a_3[/tex] خواهیم داشت:
[tex]a_3=2a_2 4a_1 p_1 1[/tex][tex]p_1=0[/tex] خواهد بود و خواهیم داشت:
[tex]a_3=2a_2 4a_1 1[/tex]ولی اگه در [tex]p_n[/tex] ، سیگما از i=0 شروع بشه [tex]p_1=2a_0[/tex] خواهد شد و برای تمام n ها هم اون ۲ حالتی که n-1 رقم ۲ هست و رقم آخر ۰ یا ۳ هست رو لحاظ میکنه
[tex]a_3=43[/tex]
بله درسته. متوجه شدم. چون مقدار P از عبارت حذف شده بود دقت نکردم.
[tex]a_3=3a_2 2a_1-2a_0=3*13 2*4-2*1=39 8-2=45[/tex]
۰
-۱
ارسال: #۸
Re: رابطه بازگشتی برای دنباله های n رقمی باشرط؟
سلام.
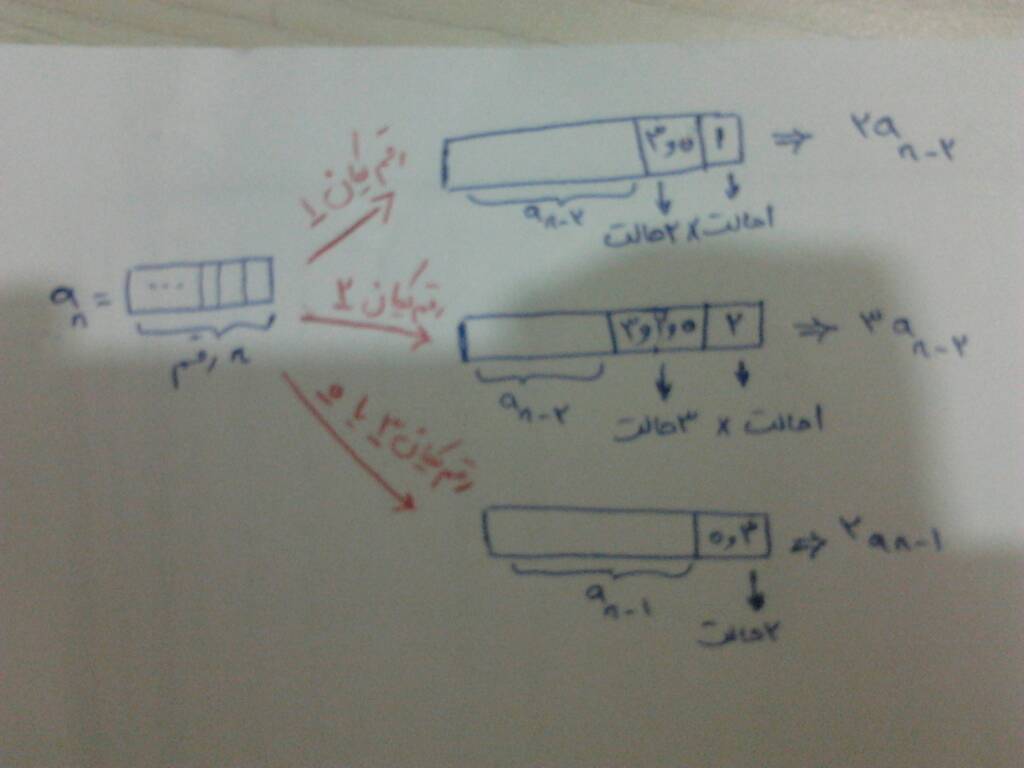
اگر an تعداد رشته های n رقمی باشه که از ۰ و ۱ و ۲ و ۳ تشکیل شده و شامل دنباله های ۱۲ و ۲۱ و ۱۱ نباشد. میشه گفت این رشته ها سه دسته اند. رشته هایی که با ۱ ختم میشوند و رشته هایی که با ۲ ختم میشوند و رشته هایی که با ۳ و ۴ ختم میشوند.
تعداد رشته هایی که با ۱ ختم میشوند ۲-۲an هست چرا که رقم قبلی یک باید ۱ یا ۲ نباشه یعنی یا ۰ باشه یا ۳/و ۲-n رقم قبلی هم بطور بازگشتی همین شرایط رو خواهد داشت که به تعداد an-2 حالت خواهد بود.یعنی تعداد رشته های ۲ - nرقمی که شامل ۰ ۱ ۲ ۳ باشه و اون دنباله ها رو نداشته باشه.
بهمین ترتیب تعداد رشته هایی که به ۲ ختم میشوند ۲-۳anتاس. رقم قبلی دو باید یا ۰ یا ۲ یا ۳ باشه.یعنی سه حالت ممکن برای رقم دهگان موجوده. و برای ۲-n رقم قبلی هم که باز ۲-an تا.
و اگه به رقم ۳ یا ۰ ختم بشه هم که ۱-۲an حالت. چرا که رقم یکان دو حالت داره و محدودیتی برای رقم قبلیشان وجود نداره و ۱-n رقم قبلی هم که همین شرایط رو خواهد داشت و به تعداد ۱-an
پس کلن رابطه بازگشتی میشه:
an=5an-2 + 2an-1
تو عکس هم واضحتر نشون دادم. امیدوارم توضیحاتم کامل باشه
اگر an تعداد رشته های n رقمی باشه که از ۰ و ۱ و ۲ و ۳ تشکیل شده و شامل دنباله های ۱۲ و ۲۱ و ۱۱ نباشد. میشه گفت این رشته ها سه دسته اند. رشته هایی که با ۱ ختم میشوند و رشته هایی که با ۲ ختم میشوند و رشته هایی که با ۳ و ۴ ختم میشوند.
تعداد رشته هایی که با ۱ ختم میشوند ۲-۲an هست چرا که رقم قبلی یک باید ۱ یا ۲ نباشه یعنی یا ۰ باشه یا ۳/و ۲-n رقم قبلی هم بطور بازگشتی همین شرایط رو خواهد داشت که به تعداد an-2 حالت خواهد بود.یعنی تعداد رشته های ۲ - nرقمی که شامل ۰ ۱ ۲ ۳ باشه و اون دنباله ها رو نداشته باشه.
بهمین ترتیب تعداد رشته هایی که به ۲ ختم میشوند ۲-۳anتاس. رقم قبلی دو باید یا ۰ یا ۲ یا ۳ باشه.یعنی سه حالت ممکن برای رقم دهگان موجوده. و برای ۲-n رقم قبلی هم که باز ۲-an تا.
و اگه به رقم ۳ یا ۰ ختم بشه هم که ۱-۲an حالت. چرا که رقم یکان دو حالت داره و محدودیتی برای رقم قبلیشان وجود نداره و ۱-n رقم قبلی هم که همین شرایط رو خواهد داشت و به تعداد ۱-an
پس کلن رابطه بازگشتی میشه:
an=5an-2 + 2an-1
تو عکس هم واضحتر نشون دادم. امیدوارم توضیحاتم کامل باشه

-۱
ارسال: #۹
RE: رابطه بازگشتی برای دنباله های n رقمی باشرط؟
[tex]A(n)=2A(n-1) 5A(n-2)\: ;\: A(1)=4,A(2)=13[/tex]
عنصر آخر اگر ۰ یا ۳ باشد جواب را برای n-1 عنصر دیگر به صورت بازگشتی می یابیم و اگر عنصر آخر ۱ باشد عنصر قبلی آن باید ۳ یا ۰ باشد و اگر عنصر آحر ۲ باشد عنصر قیلی می تواند ۲ یا ۳ یا ۰ باشد که مجموعا ۵ بار n-2 را بازگشنی حل می کنیم
عنصر آخر اگر ۰ یا ۳ باشد جواب را برای n-1 عنصر دیگر به صورت بازگشتی می یابیم و اگر عنصر آخر ۱ باشد عنصر قبلی آن باید ۳ یا ۰ باشد و اگر عنصر آحر ۲ باشد عنصر قیلی می تواند ۲ یا ۳ یا ۰ باشد که مجموعا ۵ بار n-2 را بازگشنی حل می کنیم
Can I see some ID?
Feeling left out?
نگران نباش، فقط روی این لینک برای ثبت نام کلیک کن. رمزت رو فراموش کردی؟ اینجا به یادت میاریم! close


