۰
subtitle
ارسال: #۱
حل تمرین کتاب لینز-بخش ۲-۲
با عرض سلام خدمت تمام دوستان مانشتی
همونطور که می دونیم حل تمرین های کتاب لینز از اهمیت زیادی برای یادگیری مطالب درس نظریه زبان ها و ماشین ها برخورداره.از اونجایی که حل تمرین های این کتاب بصورت یکجا و با زبان شیرین فارسی توی نت وجود نداشت(منکه چیزی نیافتم به غیر از جزوات دستنویس دوستانی که در کلاس های کنکور شرکت می کنند) بر آن شدم که حل تمرین ها ی هر بخش رو بصورت جدا هر کدام در یک تاپیک قرار بدم.
البته قاعدتا به تنهایی از عهده حل تمامی تمارین بر نخواهم آمد.اما نظرم این بوده که با کمک دوستان این سری تاپیک ها رو کامل کنیم.
*توضیح در مورد راه حل ها*
۱- سوالاتی که باید در اون اثبات صورت بگیره فعلا در دستور کار قرار نداره
۲-اگر جوابی احیاناً اشتباه بود با پیام خصوصی لطف کنید اطلاع بدید تا در سریع ترین زمان ممکن اصلاح نمایم.
۳-اینکه در انتهای تاپیک چند ارسال بصورت شماره سوال بعلاوه چند ستاره گذاشته ام(۱۵-***) بخاطر اینه که بعد از ارسال یک پاسخ فوراً نمیشه ارسال جدیدی انجام داد و ارسال های جدید در داخل ارسال قبلی قرار میگیرند.بخاطر همین ارسال ها رو موقتا ایجاد کرده ام.
۴-شاید این مورد خیلی بدیهی باشه ولی خوب شاید هم بکار بیاد چون دوستان به اون اشاره کردند:برای مشاهده جواب بر روی تصویر پیوست شده کلیک کنید تا با کیفیت کامل در صفحه ای جدید نمایش داده بشه.
۵-دوستان لطف کنند جهت تشکر از دکمه مربوطه استفاده کنند تا جواب ها بصورت متوالی بوسیله هر ارسال نمایش داده شود.(جهت پرسیدن سوال و یا انتقاد و پیشنهاد از پیام خصوصی استفاده شود. پیام هایی که احتمال استفاده شون بره در تاپیک قرار داده خواهد شد)
سوالات
۱- با تمام جزئیات، ادعای عنوان شده در بخش قبلی را ثابت کنید که اگر در یک گراف انتقال راهی با برچسب w وجود داشته باشد، آنگاه باید راهی با برچسب w با طول نابیشتر از[tex]\Lambda \left ( 1 \Lambda \right )\left | w \right |[/tex] موجود باشد.
***حل نشده***
همونطور که می دونیم حل تمرین های کتاب لینز از اهمیت زیادی برای یادگیری مطالب درس نظریه زبان ها و ماشین ها برخورداره.از اونجایی که حل تمرین های این کتاب بصورت یکجا و با زبان شیرین فارسی توی نت وجود نداشت(منکه چیزی نیافتم به غیر از جزوات دستنویس دوستانی که در کلاس های کنکور شرکت می کنند) بر آن شدم که حل تمرین ها ی هر بخش رو بصورت جدا هر کدام در یک تاپیک قرار بدم.
البته قاعدتا به تنهایی از عهده حل تمامی تمارین بر نخواهم آمد.اما نظرم این بوده که با کمک دوستان این سری تاپیک ها رو کامل کنیم.
*توضیح در مورد راه حل ها*
۱- سوالاتی که باید در اون اثبات صورت بگیره فعلا در دستور کار قرار نداره
۲-اگر جوابی احیاناً اشتباه بود با پیام خصوصی لطف کنید اطلاع بدید تا در سریع ترین زمان ممکن اصلاح نمایم.
۳-اینکه در انتهای تاپیک چند ارسال بصورت شماره سوال بعلاوه چند ستاره گذاشته ام(۱۵-***) بخاطر اینه که بعد از ارسال یک پاسخ فوراً نمیشه ارسال جدیدی انجام داد و ارسال های جدید در داخل ارسال قبلی قرار میگیرند.بخاطر همین ارسال ها رو موقتا ایجاد کرده ام.
۴-شاید این مورد خیلی بدیهی باشه ولی خوب شاید هم بکار بیاد چون دوستان به اون اشاره کردند:برای مشاهده جواب بر روی تصویر پیوست شده کلیک کنید تا با کیفیت کامل در صفحه ای جدید نمایش داده بشه.
۵-دوستان لطف کنند جهت تشکر از دکمه مربوطه استفاده کنند تا جواب ها بصورت متوالی بوسیله هر ارسال نمایش داده شود.(جهت پرسیدن سوال و یا انتقاد و پیشنهاد از پیام خصوصی استفاده شود. پیام هایی که احتمال استفاده شون بره در تاپیک قرار داده خواهد شد)
سوالات
۱- با تمام جزئیات، ادعای عنوان شده در بخش قبلی را ثابت کنید که اگر در یک گراف انتقال راهی با برچسب w وجود داشته باشد، آنگاه باید راهی با برچسب w با طول نابیشتر از[tex]\Lambda \left ( 1 \Lambda \right )\left | w \right |[/tex] موجود باشد.
***حل نشده***
۱
ارسال: #۲
RE: حل تمرین کتاب لینز-بخش ۲-۲
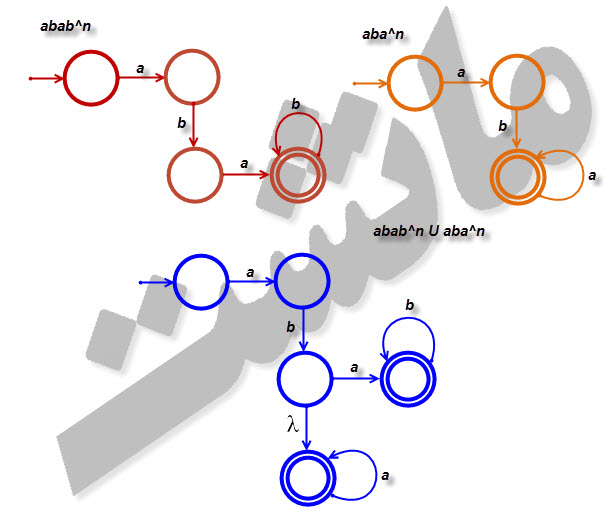
۷- یک پذیرنده متناهی غیرقطعی با حداکثر پنج حالت برای مجموعه [tex]\left \{ abab^{n}:n\geqslant 0 \right \}\cup \left \{ aba^{n}:n\geqslant 0 \right \}[/tex] طراحی کنید.

۱
ارسال: #۳
حل تمرین کتاب لینز-بخش ۲-۲
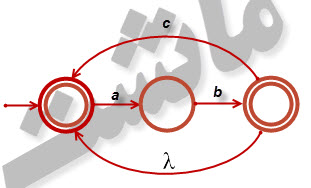
۸-یک پذیرنده متناهی غیرقطعی با سه حالت بسازید که زبان [tex]\left \{ ab,abc \right \}^{*}[/tex] را بپذیرد.

۰
ارسال: #۴
حل تمرین کتاب لینز-بخش ۲-۲
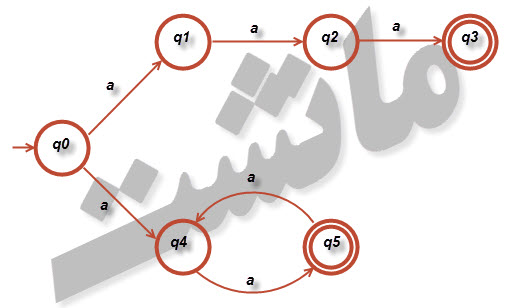
۲- یک پذیرنده متناهی قطعی بیابید که زبان تعریف شده بوسیله پذیرنده متناهی غیر قطعی در شکل ۲-۸ را بپذیرد.
شکل ۲-۸
جواب

شکل ۲-۸

جواب

۰
ارسال: #۵
حل تمرین کتاب لینز-بخش ۲-۲
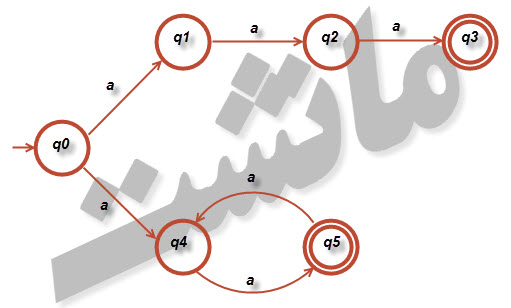
۳- یک پذیرنده متناهی قطعی بیابید که مکمل زبان تعریف شده بوسیله پذیرنده متناهی غیر قطعی در شکل ۲-۸ را بپذیرد.
شکل ۲-۸
جواب

شکل ۲-۸

جواب

۰
ارسال: #۶
حل تمرین کتاب لینز-بخش ۲-۲
۴ -در شکل ۲-۹ توابع [tex]\delta ^{*}\left ( q_{0},1011 \right )[/tex] و [tex]\delta ^{*}\left ( q_{1},01 \right )[/tex] را بیابید.
شکل ۲-۹
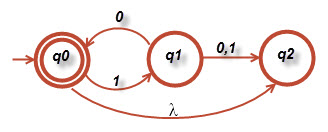
جواب الف
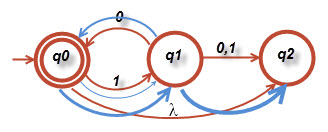
جواب ب
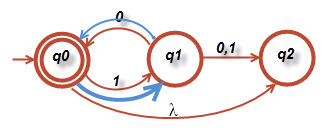
شکل ۲-۹

جواب الف

جواب ب

۰
ارسال: #۷
حل تمرین کتاب لینز-بخش ۲-۲
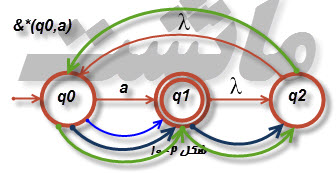
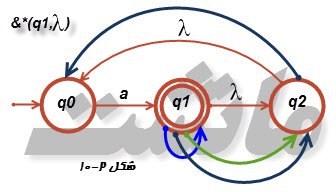
۵-در شکل ۲-۱۰، [tex]\delta ^{*}\left ( q_{0},a \right )[/tex] و [tex]\delta ^{*}\left ( q_{1},\lambda \right )[/tex] را بیابید.
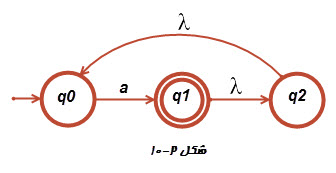



۰
ارسال: #۸
حل تمرین کتاب لینز-بخش ۲-۲
۶-برای پذیرنده متناهی غیرقطعی در شکل ۲-۹، [tex]\delta ^{*}\left ( q_{0},1010 \right )[/tex] و [tex]\delta ^{*}\left ( q_{1},00 \right )[/tex] را بیابید.
الف)
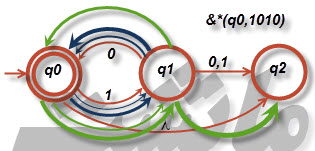
ب) [tex]\delta ^{*}(q_{0},00)=\varnothing[/tex]
الف)

ب) [tex]\delta ^{*}(q_{0},00)=\varnothing[/tex]
۰
ارسال: #۹
RE: حل تمرین کتاب لینز-بخش ۲-۲
۹- آیا فکر میکنید تمرین ۸ میتواند با کمتر از ۳ حالت حل شود؟
خیر. از آنجایی که الفبای ما شامل ۳ عضو است، جهت تولید این زبان حداقل به ۳ حالت متمایز نیاز است.
خیر. از آنجایی که الفبای ما شامل ۳ عضو است، جهت تولید این زبان حداقل به ۳ حالت متمایز نیاز است.
ارسال: #۱۰
RE: حل تمرین کتاب لینز-بخش ۲-۲
(۰۶ آذر ۱۳۹۱ ۰۳:۵۴ ب.ظ)hp1361 نوشته شده توسط: ۱۰-یک پذیرنده متناهی غیرقطعی با چهارحالت برای [tex]L=\left \{ a^{n}:n\geq 0 \right \}\cup \left \{ b^{n}a:n\geq 1 \right \}[/tex] بیابید.دوست عزیزم ممنون که وقت میزاری و این تصاویر با کیفیت رو میزاری برا بچه ها
۱۱-****
من فایرفاکسم خطا میداد اکسپشن و نشون نمیداد تصاویر رو
تنظیمش کردم الان نشون میده ممنون پیام دادین همینطور ممنونم از eternal عزیز که ایشون هم نکته شما رو گفتن مرسی عالی بودند تصاویر
۰
ارسال: #۱۱
حل تمرین کتاب لینز-بخش ۲-۲
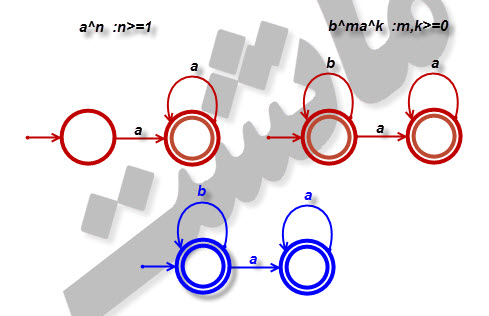
۱۰-الف)یک پذیرنده متناهی غیرقطعی با سه حالت بیابید که زبان [tex]L= \left \{ a^{n}:n\geq 1 \right \}\cup \left \{ b^{m}a^{k}:m\geq 0,k\geq0 \right \}[/tex] را بپذیرد.
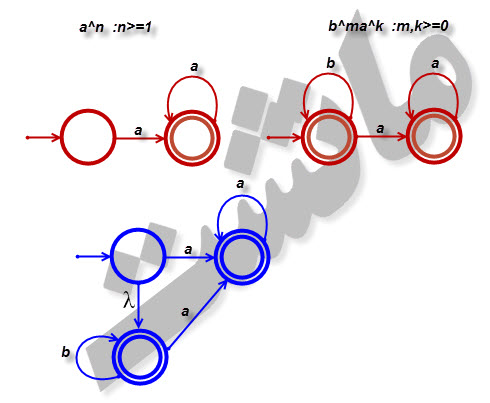
ب)آیا فکر میکنید که زبان بخش الف می تواند بوسیله یک پذیرنده متناهی غیرقطعی با کمتر از سه حالت پذیرفته شود؟
پاسخ: بله. زبان [tex]\left \{ a^{n}:n\geq 1 \right \}[/tex] درون زبان [tex]\left \{ b^{m}a^{k}:m,k\geq 0 \right \}[/tex] وجود دارد.

ب)آیا فکر میکنید که زبان بخش الف می تواند بوسیله یک پذیرنده متناهی غیرقطعی با کمتر از سه حالت پذیرفته شود؟
پاسخ: بله. زبان [tex]\left \{ a^{n}:n\geq 1 \right \}[/tex] درون زبان [tex]\left \{ b^{m}a^{k}:m,k\geq 0 \right \}[/tex] وجود دارد.

۰
ارسال: #۱۲
حل تمرین کتاب لینز-بخش ۲-۲
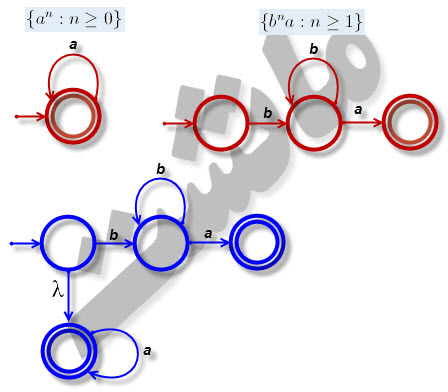
۱۱-یک پذیرنده متناهی غیرقطعی با چهارحالت برای [tex]L=\left \{ a^{n}:n\geq 0 \right \}\cup \left \{ b^{n}a:n\geq 1 \right \}[/tex] بیابید.

۰
ارسال: #۱۳
حل تمرین کتاب لینز-بخش ۲-۲
۱۲ -کدامیک از رشته های ۰۰، ۰۱۰۰۱، ۱۰۰۱۰، ۰۰۰، ۰۰۰۰ بوسیله پذیرنده متناهی قطعی زیر پذیرفته می شود؟
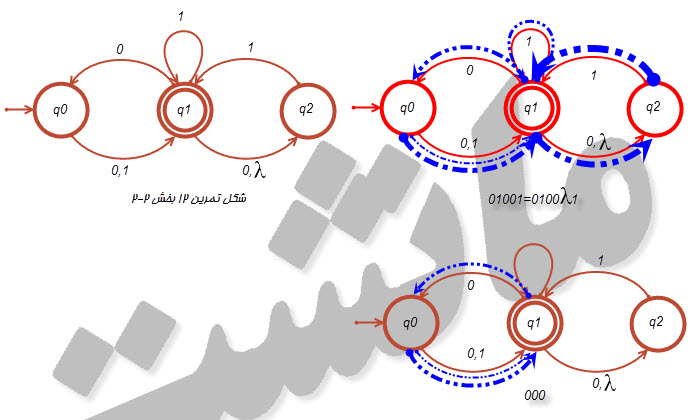
سوال : زبان پذیرفته شده توسط این ماشین چیست؟

سوال : زبان پذیرفته شده توسط این ماشین چیست؟
۰
ارسال: #۱۴
حل تمرین کتاب لینز-بخش ۲-۲
۱۳ - مکمل زبان پذیرفته شده بوسیله پذیرنده متناهی غیر قطعی در شکل ۲-۱۰ چیست ؟

۰
ارسال: #۱۵
حل تمرین کتاب لینز-بخش ۲-۲
۱۴ - فرض کنید [tex]L[/tex] زبان پذیرفته شده بوسیله پذیرنده متناهی غیر قطعی در شکل ۲-۸ باشد. یک پذیرنده متناهی غیر قطعی بیابید که [tex]L \cup \left \{ a^{5} \right \}[/tex] را بپذیرد.
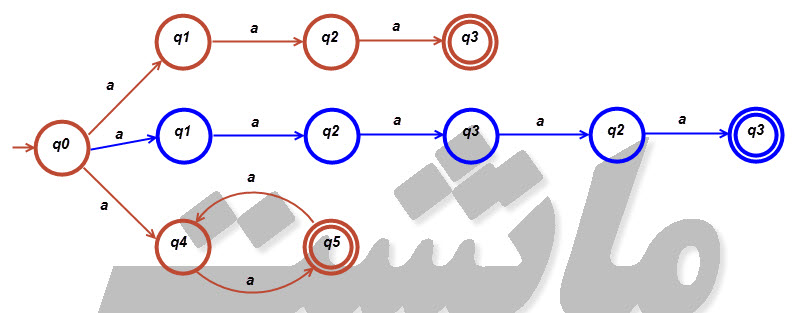
سوال : پذیرنده متناهی قطعی این زبان را رسم کنید.

سوال : پذیرنده متناهی قطعی این زبان را رسم کنید.
۰
ارسال: #۱۶
حل تمرین کتاب لینز-بخش ۲-۲
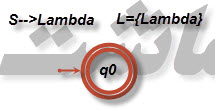
۱۵ - توصیف ساده ای از زبان تمرین ۱۳ ارائه دهید.
زبان این پذیرنده [tex]L=\left \{ \lambda \right \}[/tex] می باشد. یعنی فقط رشته به طول صفر پذیرفته و در همان وضعیت ابتدایی قرار می گیرد که وضعیت نهایی است.
زبان این پذیرنده [tex]L=\left \{ \lambda \right \}[/tex] می باشد. یعنی فقط رشته به طول صفر پذیرفته و در همان وضعیت ابتدایی قرار می گیرد که وضعیت نهایی است.
۰
ارسال: #۱۷
حل تمرین کتاب لینز-بخش ۲-۲
۱۶ - یک پذیرنده متناهی غیر قطعی بیابید که [tex]\left \{ a \right \}^{*}[/tex] را بپذیرد بطوریکه اگر در گراف انتقال آن یک یال تنها حذف شود (بدون هیچگونه تغییر دیگری)، ماشین بدست آمده [tex]\left \{ a \right \}[/tex] را بپذیرد.
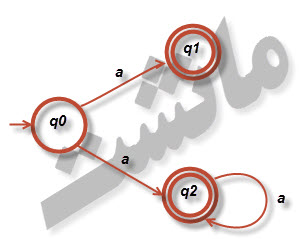
سوال : برای این تمرین آیا میتوان پذیرنده متناهی غیر قطعی ای ساخت که از بین یال ها هر کدام که حذف شود همین نتیجه را بدهد؟

سوال : برای این تمرین آیا میتوان پذیرنده متناهی غیر قطعی ای ساخت که از بین یال ها هر کدام که حذف شود همین نتیجه را بدهد؟
ارسال: #۱۸
RE: حل تمرین کتاب لینز-بخش ۲-۲
(۰۷ آذر ۱۳۹۱ ۰۲:۴۹ ب.ظ)hp1361 نوشته شده توسط: ۱۶ - یک پذیرنده متناهی غیر قطعی بیابید که [tex]\left \{ a \right \}^{*}[/tex] را بپذیرد بطوریکه اگر در گراف انتقال آن یک یال تنها حذف شود (بدون هیچگونه تغییر دیگری)، ماشین بدست آمده [tex]\left \{ a \right \}[/tex] را بپذیرد.
سوال : برای این تمرین آیا میتوان پذیرنده متناهی غیر قطعی ای ساخت که از بین یال ها هر کدام که حذف شود همین نتیجه را بدهد؟
با سلام
این ماشین الان لاندا را میپذیرد؟
چون قرار است {a}* را بپذیرد که خوب شامل لاندا هم هست...
۰
ارسال: #۱۹
حل تمرین کتاب لینز-بخش ۲-۲
۱۷ - آیا تمرین ۱۶ می تواند با استفاده از یک پذیرنده متناهی قطعی حل شود؟ اگر چنین است،راه حل را ارائه دهید، اگر نیست استدلالاتی قانع کننده برای نتیجه خود ارائه دهید.
جواب : خیر. از آنجائیکه زبان [tex]\left \{ a \right \}^{*}[/tex] شامل [tex]\lambda[/tex] می باشد، با حذف هیچ یالی این رشته از بین نخواهد رفت و لذا با حذف هر کدام از یال های هر ماشین متناهی قطعی ای کماکان این رشته تولید خواهد شد که با خواسته سوال که تولید صرفاً [tex]\left \{ a \right \}[/tex] می باشد متضاد است.
جواب : خیر. از آنجائیکه زبان [tex]\left \{ a \right \}^{*}[/tex] شامل [tex]\lambda[/tex] می باشد، با حذف هیچ یالی این رشته از بین نخواهد رفت و لذا با حذف هر کدام از یال های هر ماشین متناهی قطعی ای کماکان این رشته تولید خواهد شد که با خواسته سوال که تولید صرفاً [tex]\left \{ a \right \}[/tex] می باشد متضاد است.
۰
ارسال: #۲۰
حل تمرین کتاب لینز-بخش ۲-۲
۱۸- تغییرات زیر را برای تعریف ۲-۶ در نظر بگیرید. یک nfa با چندین وضعیت ابتدایی بصورت پنج تایی [tex]M=\left ( Q,\Sigma ,\delta ,Q_{0},F \right )[/tex] تعریف می شود که در آن [tex]Q_{0}\subseteq Q[/tex] مجموعه ای از وضعیت های ابتدایی ممکن است. زبان پذیرفته شده توسط چنین ماشینی بصورت زیر تعیف می شود:
[tex]L\left ( M \right )=\left \{ w:\delta ^{*}\left ( q_{0},w \right ) contains \: q_{f}\: ,\: for \: any \: q_{0}\in Q_{0} \: , \: q_{f}\in F \right \}[/tex]
نشان دهید برای هر nfa با چندین وضعیت ابتدایی یک nfa با یک وضعیت ابتدایی وجود دارد که همان زبان را می پذیرد.
جواب : کافیست یک وضعیت شروع جدید [tex]p_{0}[/tex] تعریف نموده و با یک [tex]\lambda[/tex] به هریک از وضعیت های شروع قبلی وصل نمائیم. همچنین وضعیت های شروع قبلی را از حالت شروع خارج نمائیم.(چراکه حالا در ادامه وضعیت شروع جدید قرار دارند)
[tex]\delta (p_{0},\lambda )=Q_{0}[/tex]
[tex]L\left ( M \right )=\left \{ w:\delta ^{*}\left ( q_{0},w \right ) contains \: q_{f}\: ,\: for \: any \: q_{0}\in Q_{0} \: , \: q_{f}\in F \right \}[/tex]
نشان دهید برای هر nfa با چندین وضعیت ابتدایی یک nfa با یک وضعیت ابتدایی وجود دارد که همان زبان را می پذیرد.
جواب : کافیست یک وضعیت شروع جدید [tex]p_{0}[/tex] تعریف نموده و با یک [tex]\lambda[/tex] به هریک از وضعیت های شروع قبلی وصل نمائیم. همچنین وضعیت های شروع قبلی را از حالت شروع خارج نمائیم.(چراکه حالا در ادامه وضعیت شروع جدید قرار دارند)
[tex]\delta (p_{0},\lambda )=Q_{0}[/tex]
۰
ارسال: #۲۱
حل تمرین کتاب لینز-بخش ۲-۲
۱۹ - فرض کنید در تمرین ۱۸ محدودیت [tex]Q_{0}\cap F=\varnothing[/tex] را اعمال کنیم. آیا این محدودیت تاثیری در نتیجه دارد؟
جواب : خیر. اینکه با استفاده از یک وضعیت شروع واحد به نقاط شروع قبلی برسیم ارتباطی با این ندارد که آن وضعیت ها پایانی باشند یا خیر.
جواب : خیر. اینکه با استفاده از یک وضعیت شروع واحد به نقاط شروع قبلی برسیم ارتباطی با این ندارد که آن وضعیت ها پایانی باشند یا خیر.
۰
ارسال: #۲۲
حل تمرین کتاب لینز-بخش ۲-۲
۲۰ - با استفاده از تعریف ۲-۵ نشان دهید که برای هر nfa رابطه زیر برقرار است:
[tex]\delta ^{*}\left ( q,wv \right )=\bigcup_{p\in \delta ^{*}\left ( q,w \right )} \delta ^{*}\left ( p,v \right )[/tex]
[tex]for \: all \: q \in Q \: and \: all \: w,v \in \Sigma ^{*}[/tex]
تعریف ۲-۵
[tex]for \; an \; nfa , \; the \; extended \; transition \; function \; is \; defined \; so \; that \; \delta ^{*}\left ( q_{i},w \right ) \; contains \\ \; q_{j} \; if \; and \; only \; if \; there \; is \; a \; walk \; in \; the \; transition \; graph \; from \; q_{i} \; to \; q_{j} \; labeled \; w.\\ \; this \; holds \; for \; all \; q_{i},q_{j}\in Q \; and \; w \in \Sigma ^{*}[/tex]
***حل نشده***
[tex]\delta ^{*}\left ( q,wv \right )=\bigcup_{p\in \delta ^{*}\left ( q,w \right )} \delta ^{*}\left ( p,v \right )[/tex]
[tex]for \: all \: q \in Q \: and \: all \: w,v \in \Sigma ^{*}[/tex]
تعریف ۲-۵
[tex]for \; an \; nfa , \; the \; extended \; transition \; function \; is \; defined \; so \; that \; \delta ^{*}\left ( q_{i},w \right ) \; contains \\ \; q_{j} \; if \; and \; only \; if \; there \; is \; a \; walk \; in \; the \; transition \; graph \; from \; q_{i} \; to \; q_{j} \; labeled \; w.\\ \; this \; holds \; for \; all \; q_{i},q_{j}\in Q \; and \; w \in \Sigma ^{*}[/tex]
***حل نشده***
۰
ارسال: #۲۳
RE: حل تمرین کتاب لینز-بخش ۲-۲
۲۱- یک پذیرنده متناهی غیر قطعی (nfa) که الف) دارای هیچ انتقالات [tex]\lambda[/tex] نباشد و ب) برای همه [tex]q \in Q[/tex] و همه [tex]a \in \Sigma[/tex]، [tex]\delta \left ( q,a \right )[/tex] شامل حداکثر یک عنصر باشد، گاهی اوقات یک پذیرنده متناهی قطعی غیرکامل نامیده می شود. این امر معقول است زیرا شرایطی قابل تصور است که هیچ انتخابی جهت حرکت وجود نداشته باشد. برای [tex]\Sigma =\left \{ a,b \right \}[/tex]، پذیرنده متناهی قطعی غیرکامل زیر را به یک پذیرنده متناهی قطعی استاندارد تبدیل کنید.
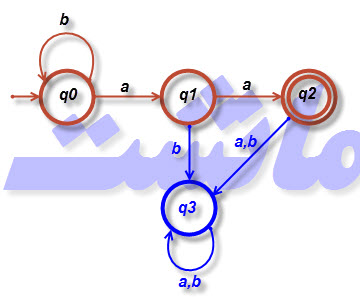
توضیح : در پذبرنده متناهی قطعی غیرکامل، با توجه به اینکه [tex]\lambda[/tex] و یال تکراری وجود ندارد، لذا جهت تبدیل آن به یک dfa، تنها کاری که لازم است انجام دهیم، تعریف یک تله جهت هدایت یال های تعریف نشده به آن می باشد.

توضیح : در پذبرنده متناهی قطعی غیرکامل، با توجه به اینکه [tex]\lambda[/tex] و یال تکراری وجود ندارد، لذا جهت تبدیل آن به یک dfa، تنها کاری که لازم است انجام دهیم، تعریف یک تله جهت هدایت یال های تعریف نشده به آن می باشد.
۰
ارسال: #۲۴
حل تمرین کتاب لینز-بخش ۲-۲
توی حل سوال ۲
شکل ۲-۸
توی جوابش اصلا احتیاج به آوردن b نبود.به هر حال خلاصه ترم میشد. بد نبود یه توضیحم بنویسی تا دیگه بقیه روی اون b ها شک نکنن.
سعی کنید این مباحث رو ادامه ندید و بیشتر تست هایی رو بیارید+نکات مهم کنکوری.البته ناراحت نشیدا. از اون طرف هم خودتون ببینید مباحثش خیلی مبتدی هست.
شکل ۲-۸
توی جوابش اصلا احتیاج به آوردن b نبود.به هر حال خلاصه ترم میشد. بد نبود یه توضیحم بنویسی تا دیگه بقیه روی اون b ها شک نکنن.
سعی کنید این مباحث رو ادامه ندید و بیشتر تست هایی رو بیارید+نکات مهم کنکوری.البته ناراحت نشیدا. از اون طرف هم خودتون ببینید مباحثش خیلی مبتدی هست.
Can I see some ID?
Feeling left out?
نگران نباش، فقط روی این لینک برای ثبت نام کلیک کن. رمزت رو فراموش کردی؟ اینجا به یادت میاریم! close



