۰
subtitle
ارسال: #۱
حل تمرین کتاب لینز-بخش ۲-۱
با عرض سلام خدمت تمام دوستان مانشتی
همونطور که می دونیم حل تمرین های کتاب لینز از اهمیت زیادی برای یادگیری مطالب درس نظریه زبان ها و ماشین ها برخورداره.از اونجایی که حل تمرین های این کتاب بصورت یکجا و با زبان شیرین فارسی توی نت وجود نداشت(منکه چیزی نیافتم به غیر از جزوات دستنویس دوستانی که در کلاس های کنکور شرکت می کنند) بر آن شدم که حل تمرین ها ی هر بخش رو بصورت جدا هر کدام در یک تاپیک قرار بدم.
البته قاعدتا به تنهایی از عهده حل تمامی تمارین بر نخواهم آمد.اما نظرم این بوده که با کمک دوستان این سری تاپیک ها رو کامل کنیم.
شایان ذکر است من به عنوان کسی که کاملاً به این درس مسلط باشه اقدام به ایجاد تاپیک نکردم.در درجه اول یادگیری خودم، بعد یادگیری دوستان و بالاخره جمع آوری پاسخ سوالات کتاب جهت رفع ابهامات دوستان در تاپیک های مرتب بوده است.
*توضیح در مورد راه حل ها*
۱- سوالاتی که باید در اون اثبات صورت بگیره فعلا در دستور کار قرار نداره
۲-اگر جوابی احیاناً اشتباه بود با پیام خصوصی لطف کنید اطلاع بدید تا در سریع ترین زمان ممکن اصلاح نمایم.
۳-اینکه در انتهای تاپیک چند ارسال بصورت شماره سوال بعلاوه چند ستاره گذاشته ام(۱۵-***) بخاطر اینه که بعد از ارسال یک پاسخ فوراً نمیشه ارسال جدیدی انجام داد و ارسال های جدید در داخل ارسال قبلی قرار میگیرند.بخاطر همین ارسال ها رو موقتا ایجاد کرده ام.
۴-شاید این مورد خیلی بدیهی باشه ولی خوب شاید هم بکار بیاد چون دوستان به اون اشاره کردند:برای مشاهده جواب بر روی تصویر پیوست شده کلیک کنید تا با کیفیت کامل در صفحه ای جدید نمایش داده بشه.
۵-دوستان لطف کنند جهت تشکر از دکمه مربوطه استفاده کنند تا جواب ها بصورت متوالی بوسیله هر ارسال نمایش داده شود.(جهت پرسیدن سوال و یا انتقاد و پیشنهاد از پیام خصوصی استفاده شود. پیام هایی که احتمال استفاده شون بره در تاپیک قرار داده خواهد شد)
حل تمرین
-------------------------------
۱- ماشین زیر کدام یک از رشته های ۰۰۰۰۱ ،۰۱۰۰۱ ، ۰۰۰۰۱۱۰ را می پذیرد؟
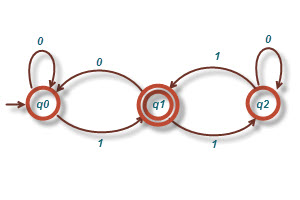
حل:
رشته ۰۰۰۰۱
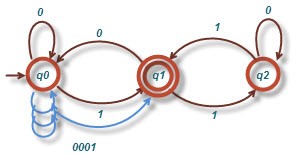
با توجه به اینکه ماشین به حالت نهایی(پایانی) رسیده، لذا این رشته رو می پذیره.
رشته ۰۱۰۰۱
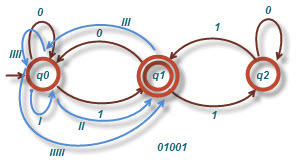
با توجه به اینکه به حالت نهایی(پایانی) رسیده، لذا این رشته رو می پذیره.
رشته ۰۰۰۰۱۱۰
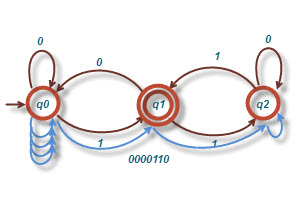
همانطور که در شکل مشخص است این رشته ماشین رو به حالت پایانی نبرده، لذا ماشین این رشته رو نمی پذیرد.
همونطور که می دونیم حل تمرین های کتاب لینز از اهمیت زیادی برای یادگیری مطالب درس نظریه زبان ها و ماشین ها برخورداره.از اونجایی که حل تمرین های این کتاب بصورت یکجا و با زبان شیرین فارسی توی نت وجود نداشت(منکه چیزی نیافتم به غیر از جزوات دستنویس دوستانی که در کلاس های کنکور شرکت می کنند) بر آن شدم که حل تمرین ها ی هر بخش رو بصورت جدا هر کدام در یک تاپیک قرار بدم.
البته قاعدتا به تنهایی از عهده حل تمامی تمارین بر نخواهم آمد.اما نظرم این بوده که با کمک دوستان این سری تاپیک ها رو کامل کنیم.
شایان ذکر است من به عنوان کسی که کاملاً به این درس مسلط باشه اقدام به ایجاد تاپیک نکردم.در درجه اول یادگیری خودم، بعد یادگیری دوستان و بالاخره جمع آوری پاسخ سوالات کتاب جهت رفع ابهامات دوستان در تاپیک های مرتب بوده است.
*توضیح در مورد راه حل ها*
۱- سوالاتی که باید در اون اثبات صورت بگیره فعلا در دستور کار قرار نداره
۲-اگر جوابی احیاناً اشتباه بود با پیام خصوصی لطف کنید اطلاع بدید تا در سریع ترین زمان ممکن اصلاح نمایم.
۳-اینکه در انتهای تاپیک چند ارسال بصورت شماره سوال بعلاوه چند ستاره گذاشته ام(۱۵-***) بخاطر اینه که بعد از ارسال یک پاسخ فوراً نمیشه ارسال جدیدی انجام داد و ارسال های جدید در داخل ارسال قبلی قرار میگیرند.بخاطر همین ارسال ها رو موقتا ایجاد کرده ام.
۴-شاید این مورد خیلی بدیهی باشه ولی خوب شاید هم بکار بیاد چون دوستان به اون اشاره کردند:برای مشاهده جواب بر روی تصویر پیوست شده کلیک کنید تا با کیفیت کامل در صفحه ای جدید نمایش داده بشه.
۵-دوستان لطف کنند جهت تشکر از دکمه مربوطه استفاده کنند تا جواب ها بصورت متوالی بوسیله هر ارسال نمایش داده شود.(جهت پرسیدن سوال و یا انتقاد و پیشنهاد از پیام خصوصی استفاده شود. پیام هایی که احتمال استفاده شون بره در تاپیک قرار داده خواهد شد)
حل تمرین
-------------------------------
۱- ماشین زیر کدام یک از رشته های ۰۰۰۰۱ ،۰۱۰۰۱ ، ۰۰۰۰۱۱۰ را می پذیرد؟

حل:
رشته ۰۰۰۰۱

با توجه به اینکه ماشین به حالت نهایی(پایانی) رسیده، لذا این رشته رو می پذیره.
رشته ۰۱۰۰۱

با توجه به اینکه به حالت نهایی(پایانی) رسیده، لذا این رشته رو می پذیره.
رشته ۰۰۰۰۱۱۰

همانطور که در شکل مشخص است این رشته ماشین رو به حالت پایانی نبرده، لذا ماشین این رشته رو نمی پذیرد.
۰
ارسال: #۲
RE: حل تمرین کتاب لینز-بخش ۲-۱
۲-روی [tex]\sum = \left \{ a,b \right \}[/tex] ،پذیرنده های متناهی قطعی بسازید که مجموعه های زیر را بپذیرد:
الف) همه رشته هایی با دقیقا یک a
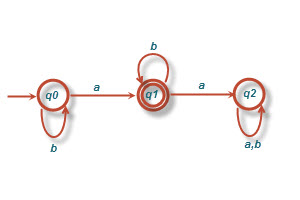
ب) همه رشته هایی با حداقل یک a
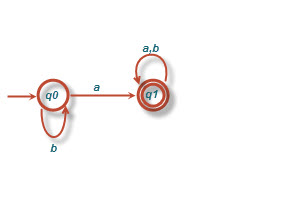
ج) همه رشته هایی که بیش از سه a ندارند(حداکثر سه a دارند)
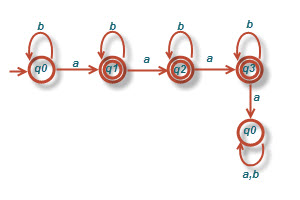
د) تمام رشته هایی با حداقل یک a و دقیقاً دو b
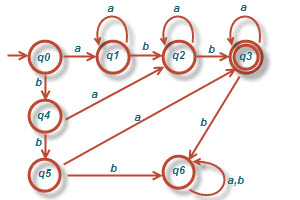
ه) همه رشته هایی با دقیقاً دو a و بیش از دو b
الف) همه رشته هایی با دقیقا یک a

ب) همه رشته هایی با حداقل یک a

ج) همه رشته هایی که بیش از سه a ندارند(حداکثر سه a دارند)

د) تمام رشته هایی با حداقل یک a و دقیقاً دو b

ه) همه رشته هایی با دقیقاً دو a و بیش از دو b

۰
ارسال: #۳
RE: حل تمرین کتاب لینز-بخش ۲-۱
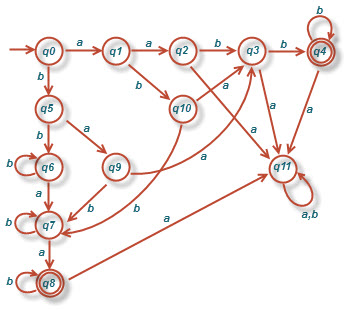
۳-نشان دهید اگر شکل زیر(۲-۶ در کتاب) را تغییر دهیم، به گونه ای که q3 به حالت غیرنهایی و q2 , q1 , q0 به حالت نهایی تبدیل شوند، پذیرنده متناهی قطعی بدست آمده، [tex]\bar{L}[/tex] را می پذیرد
***حل نشده***
۴-نتایج تمرین قبلی را تعمیم دهید.بخصوص، نشان دهید اگر [tex]M=\left ( Q,\sum ,\delta ,q0,F \right )[/tex] و [tex]\hat{M}=\left ( Q,\sum ,\delta ,q0,Q-F \right )[/tex] دو پذیرنده متناهی قطعی باشند، آنگاه [tex]\overline{L\left ( M \right )}=L\left (\hat{M} \right )[/tex]
***حل نشده***
***حل نشده***
۴-نتایج تمرین قبلی را تعمیم دهید.بخصوص، نشان دهید اگر [tex]M=\left ( Q,\sum ,\delta ,q0,F \right )[/tex] و [tex]\hat{M}=\left ( Q,\sum ,\delta ,q0,Q-F \right )[/tex] دو پذیرنده متناهی قطعی باشند، آنگاه [tex]\overline{L\left ( M \right )}=L\left (\hat{M} \right )[/tex]
***حل نشده***
۰
ارسال: #۴
RE: حل تمرین کتاب لینز-بخش ۲-۱
۵- پذیرنده متناهی قطعی برای زبانهای زیر بدهید.
الف)[tex]L=\left \{ab^{5}wb^{4}: w\epsilon\left \{ a,b \right \}\textup{*} \right \}[/tex]
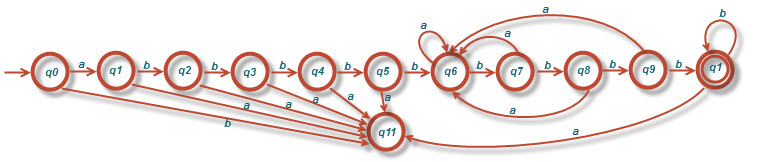
ب) [tex]L=\left \{ w_{1}abw_{2} : w_{1}\epsilon \left \{ a,b \right \}^{*} , w_{2}\epsilon \left \{ a,b \right \}^{*} \right \}[/tex]
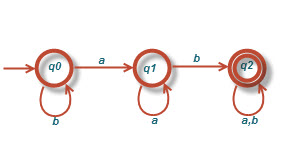
الف)[tex]L=\left \{ab^{5}wb^{4}: w\epsilon\left \{ a,b \right \}\textup{*} \right \}[/tex]

ب) [tex]L=\left \{ w_{1}abw_{2} : w_{1}\epsilon \left \{ a,b \right \}^{*} , w_{2}\epsilon \left \{ a,b \right \}^{*} \right \}[/tex]

۰
ارسال: #۵
RE: حل تمرین کتاب لینز-بخش ۲-۱
۶-یک توصیف بصورت نماد مجموعه ای برای زبانی که بوسیله ماشین نشان داده شده در دیاگرام زیر پذیرفته می شود، بدهید. آیا میتوانید توصیف متنی از این زبان ارائه دهید؟
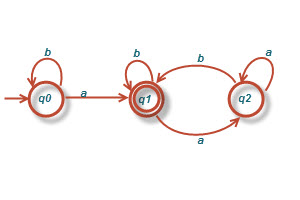
***حل نشده***

***حل نشده***
۰
ارسال: #۶
RE: حل تمرین کتاب لینز-بخش ۲-۱
۷- پذیرنده های متناهی قطعی برای زبان های زیر روی [tex]\sum =\left \{ a,b \right \}[/tex] بیابید.
الف) [tex]L=\left \{ w:\left | w \right | mod 3 =0 \right \}[/tex]
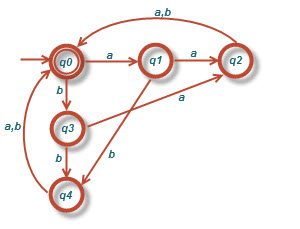
ب)[tex]L=\left \{ w:\left | w \right |mod5\neq 0 \right \}[/tex]
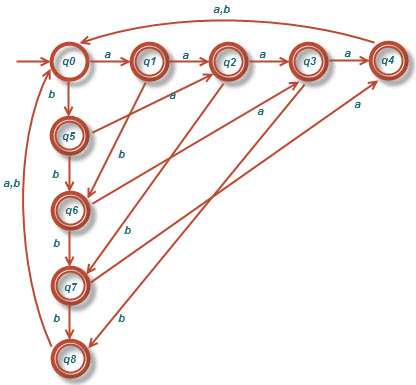
ج)[tex]L=\left \{ w:n_{a}\left ( w \right )mod3> 1 \right \}[/tex]
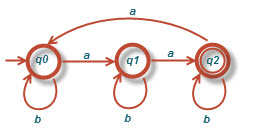
د)[tex]L=\left \{ w:n_{a}\left ( w \right )mod3>n_{b}\left ( w \right )mod3 \right \}[/tex]
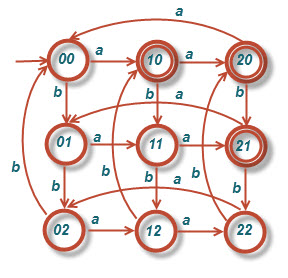
این تمرین خیلی اذیتم کرد.با اینکه به جواب نزدیک شده بودم اما تحملم تموم شد و از اینترنت جواب رو پیدا کردم!
ه)[tex]L=\left \{ w:\left ( n_{a}\left ( w \right )-n_{b}\left ( w \right ) \right )mod3>0 \right \}[/tex]
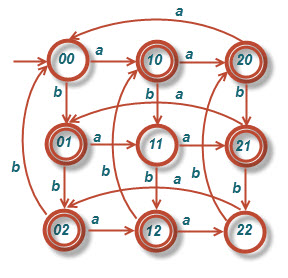
الف) [tex]L=\left \{ w:\left | w \right | mod 3 =0 \right \}[/tex]

ب)[tex]L=\left \{ w:\left | w \right |mod5\neq 0 \right \}[/tex]

ج)[tex]L=\left \{ w:n_{a}\left ( w \right )mod3> 1 \right \}[/tex]

د)[tex]L=\left \{ w:n_{a}\left ( w \right )mod3>n_{b}\left ( w \right )mod3 \right \}[/tex]

این تمرین خیلی اذیتم کرد.با اینکه به جواب نزدیک شده بودم اما تحملم تموم شد و از اینترنت جواب رو پیدا کردم!
ه)[tex]L=\left \{ w:\left ( n_{a}\left ( w \right )-n_{b}\left ( w \right ) \right )mod3>0 \right \}[/tex]

۰
ارسال: #۷
RE: حل تمرین کتاب لینز-بخش ۲-۱
سلام دوست عزیز با تشکر از شما لطفا سوال ۷ قسمت D رو هم حل کنید .کشیدن dfa برای زبانی که دقیقا دو run a به طول ۳ رو داره.با سپاس
۰
ارسال: #۸
RE: حل تمرین کتاب لینز-بخش ۲-۱
ادامه تمرین ۷
و)[tex]L=\left \{ w:\left | n_{a}\left ( w \right )-n_{b}\left ( w \right ) \right |mod3<2 \right \}[/tex]
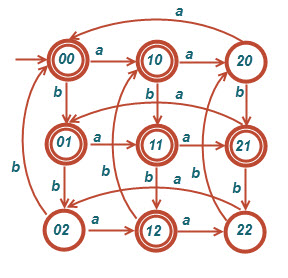
ی) [tex]L=\left \{ w: \left ( n_{a}\left ( w \right ) 2n_{b} \right \left ( w \right )) mod 3 < 2 \right \}[/tex]
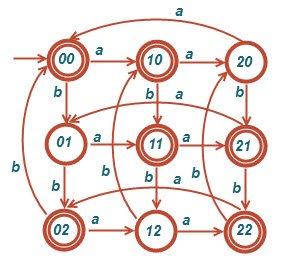
و)[tex]L=\left \{ w:\left | n_{a}\left ( w \right )-n_{b}\left ( w \right ) \right |mod3<2 \right \}[/tex]

ی) [tex]L=\left \{ w: \left ( n_{a}\left ( w \right ) 2n_{b} \right \left ( w \right )) mod 3 < 2 \right \}[/tex]

۰
ارسال: #۹
RE: حل تمرین کتاب لینز-بخش ۲-۱
۸-یک دنباله در یک رشته، یک زیر رشته با طول حداقل دو علامت یکسان است. به عنوان مثال رشته abbbaab شامل یک دنباله به طول ۳ از b ها و یک دنباله به طول ۲ از a ها می باشد. یک dfa برای زبان های زیر روی [tex]\left \{ a,b \right \}[/tex] پیدا کنید.
الف) [tex]L=\left \{ w: w\; contains\; no\; runs\; of\; length\; less\; then\; four\right \}.[/tex]
(w شامل هیچ دنباله ای به طول کمتر از ۴ نمی باشد.)
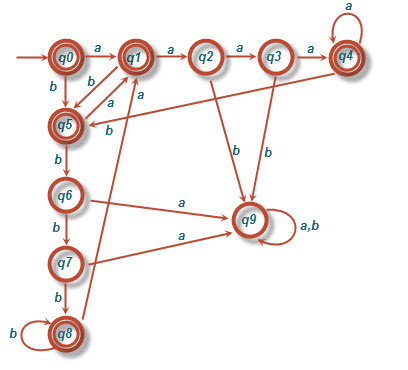
ب)[tex]L=\left \{ w:\;every\; run\; of\; a's\; has\; length\; either\; tow\; or\; three}\right \}.[/tex]
(طول هر دنباله از a ها ۲ یا ۳ باشد.)
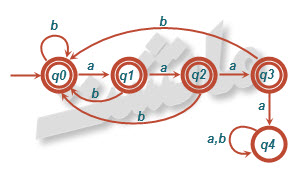
ج) [tex]L=\left \{ w: there\; are\; at\; most\; two\; runs\; of\; a's\; of\; length\; three\;\right \}.[/tex]
(حداکثر ۲ تا دنباله از a ها بطول ۳ وجود داشته باشد.)

د)[tex]L=\left \{ w: there\; are\; exactly\; two\; runs\; of\; a's\; of\; length\; 3\right \}.[/tex]
(دقیقاً ۲ دنباله با طول ۳ از a ها وجود داشته باشد.)

الف) [tex]L=\left \{ w: w\; contains\; no\; runs\; of\; length\; less\; then\; four\right \}.[/tex]
(w شامل هیچ دنباله ای به طول کمتر از ۴ نمی باشد.)

ب)[tex]L=\left \{ w:\;every\; run\; of\; a's\; has\; length\; either\; tow\; or\; three}\right \}.[/tex]
(طول هر دنباله از a ها ۲ یا ۳ باشد.)

ج) [tex]L=\left \{ w: there\; are\; at\; most\; two\; runs\; of\; a's\; of\; length\; three\;\right \}.[/tex]
(حداکثر ۲ تا دنباله از a ها بطول ۳ وجود داشته باشد.)

د)[tex]L=\left \{ w: there\; are\; exactly\; two\; runs\; of\; a's\; of\; length\; 3\right \}.[/tex]
(دقیقاً ۲ دنباله با طول ۳ از a ها وجود داشته باشد.)

۰
ارسال: #۱۰
RE: حل تمرین کتاب لینز-بخش ۲-۱
۹-مجموعه رشته های روی {۰,۱} را که طبق شروط زیر تعریف می شوند در نظر بگیرید.برای هر کدام یک dfa طراحی کنید.
الف) پس از هر ۰۰ فوراً یک ۱ بیاید.به عنوان مثال، رشته های ۱۰۱ و ۰۰۱۰ و ۰۰۱۰۰۱۱۰۰۱ در زبان هستند اما ۰۰۰۱و۰۰۱۰۰ در زبان نیستند.
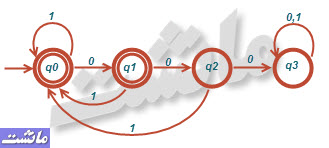
ب) همه رشته هایی که شامل ۰۰ بوده ولی شامل ۰۰۰ نباشند.
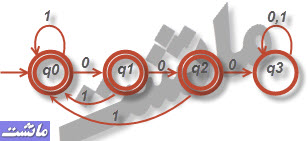
ج)سمت چپ ترین نماد با سمت راست ترین نماد متفاوت باشد.
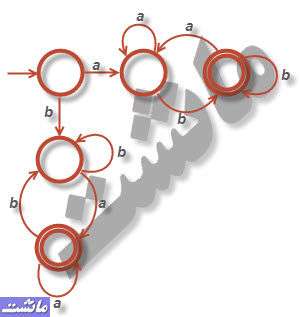
د)هر زیر رشته ای از چهار نماد که حداکثر دارای دو ۰ باشد. برای مثال، ۰۰۱۱۱۰ و ۰۱۱۰۰۱ در زبان هستند، ولی ۱۰۰۱۰ در زبان نیست زیرا یکی از زیر رشته های آن، یعنی ۰۰۱۰ دارای سه ۰ می باشد.
***حل نشده***
ه)همه رشته هایی با طول پنج یا بیشتر که در آنها چهارمین نماد از سمت راست ازچپ ترین نماد متفاوت باشد.
***حل نشده***
و)تمام رشته هایی که دو نماد سمت چپ آن با دو نماد سمت راست آن یکسان باشد.
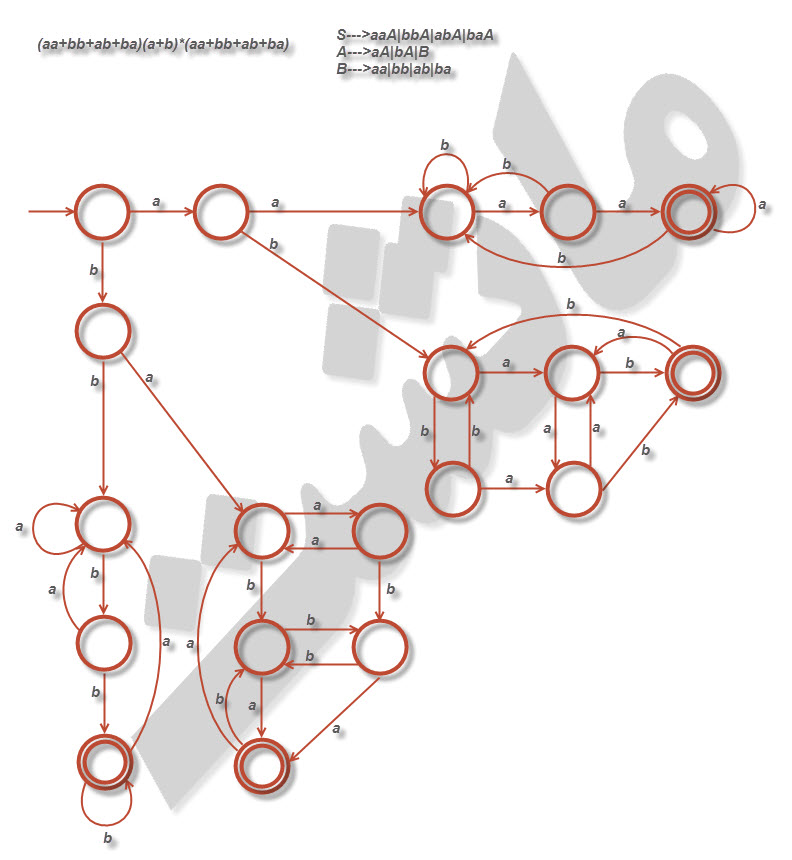
ی)تمام رشته هایی با طول ۴ یا بیشتر که ۳ نماد سمت چپ آن یکسان بوده و با سمت راست ترین نماد متفاوت باشد.
***حل نشده***
الف) پس از هر ۰۰ فوراً یک ۱ بیاید.به عنوان مثال، رشته های ۱۰۱ و ۰۰۱۰ و ۰۰۱۰۰۱۱۰۰۱ در زبان هستند اما ۰۰۰۱و۰۰۱۰۰ در زبان نیستند.

ب) همه رشته هایی که شامل ۰۰ بوده ولی شامل ۰۰۰ نباشند.

ج)سمت چپ ترین نماد با سمت راست ترین نماد متفاوت باشد.

د)هر زیر رشته ای از چهار نماد که حداکثر دارای دو ۰ باشد. برای مثال، ۰۰۱۱۱۰ و ۰۱۱۰۰۱ در زبان هستند، ولی ۱۰۰۱۰ در زبان نیست زیرا یکی از زیر رشته های آن، یعنی ۰۰۱۰ دارای سه ۰ می باشد.
***حل نشده***
ه)همه رشته هایی با طول پنج یا بیشتر که در آنها چهارمین نماد از سمت راست ازچپ ترین نماد متفاوت باشد.
***حل نشده***
و)تمام رشته هایی که دو نماد سمت چپ آن با دو نماد سمت راست آن یکسان باشد.

ی)تمام رشته هایی با طول ۴ یا بیشتر که ۳ نماد سمت چپ آن یکسان بوده و با سمت راست ترین نماد متفاوت باشد.
***حل نشده***
۰
ارسال: #۱۱
RE: حل تمرین کتاب لینز-بخش ۲-۱
۱۰- یک پذیرنده متناهی قطعی بسازید که رشته های روی {a,b} را بپذیرد، اگر و فقط اگر مقدار رشته که به عنوان نمایش دودویی از یک عدد صحیح تفسیر میشود، به پیمانه پنج برابر صفر شود(بر صف تقسیم پذیر باشد). برای مثال، ۰۱۰۱ و ۱۱۱ که به ترتیب نشان دهنده اعداد صحیح ۵ و ۱۵ می باشند، پذیرفته می شوند.
***حل نشده***
***حل نشده***
۰
ارسال: #۱۲
حل تمرین کتاب لینز-بخش ۲-۱
۱۱- نشان دهید که زبان [tex]L=\left \{ vwv:v,w \in \left \{ a,b \right \}^{*}, \left | v \right |=2 \right \}[/tex] منظم است.
برای نشان دادن اینکه زبانی منظم است کافی است برای آن یک dfa رسم کنیم لذا:
برای نشان دادن اینکه زبانی منظم است کافی است برای آن یک dfa رسم کنیم لذا:
۰
ارسال: #۱۳
حل تمرین کتاب لینز-بخش ۲-۱
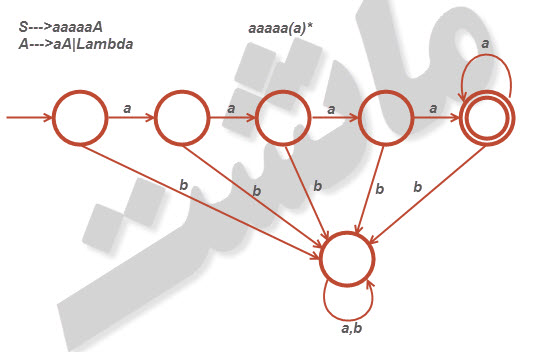
۱۲- نشان دهید که زبان [tex]L=\left \{ a^{n}:n\geqslant 4 \right \}[/tex] منظم است

۰
ارسال: #۱۴
حل تمرین کتاب لینز-بخش ۲-۱
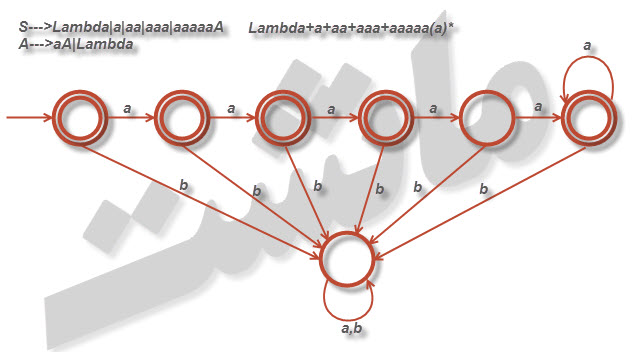
۱۳- نشان دهید که زبان [tex]L=\left \{ a^{n}:n\geqslant 0 , n\neq 4 \right \}[/tex] منظم است.

۰
ارسال: #۱۵
حل تمرین کتاب لینز-بخش ۲-۱
۱۴- نشان دهید که زبان [tex]L=\left \{ a^{n}:n\; is\; either \;a \;multiple \;of \;three \;or \;a \;multiple \;of \;five\right \}[/tex]
منظم است.(n مضربی از ۳ یا ۵ باشد)
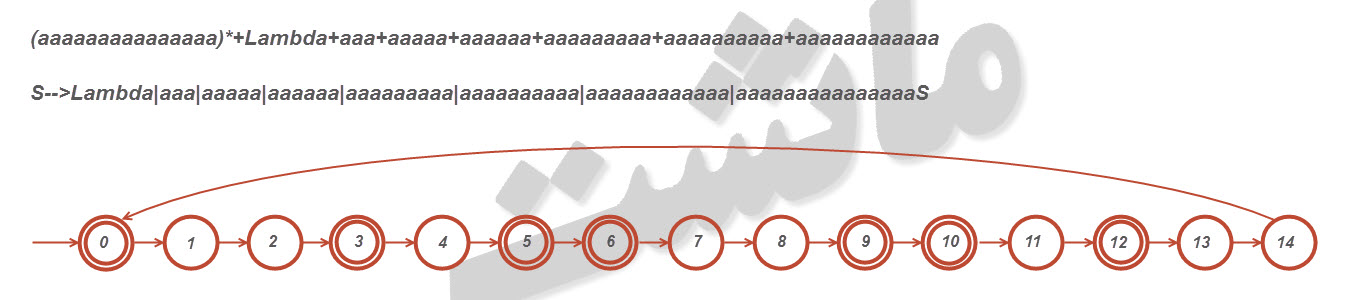
سوال: آیا برای هر زبان بصورت [tex]a^{n}[/tex] که n مضربی از x یا y باشد، نقطه x*y همان نقطه شروع است؟(تشکیل حلقه)
منظم است.(n مضربی از ۳ یا ۵ باشد)

سوال: آیا برای هر زبان بصورت [tex]a^{n}[/tex] که n مضربی از x یا y باشد، نقطه x*y همان نقطه شروع است؟(تشکیل حلقه)
۰
ارسال: #۱۶
حل تمرین کتاب لینز-بخش ۲-۱
۱۵- نشان دهید که زبان [tex]L=\left \{ a^{n}:n\; is\; a \;multiple \;of \;three,\; but\;not \;a \;multiple \;of \;five\right \}[/tex]
منظم است.(n مضربی از ۳ باشد اما مضربی از ۵ نباشد)
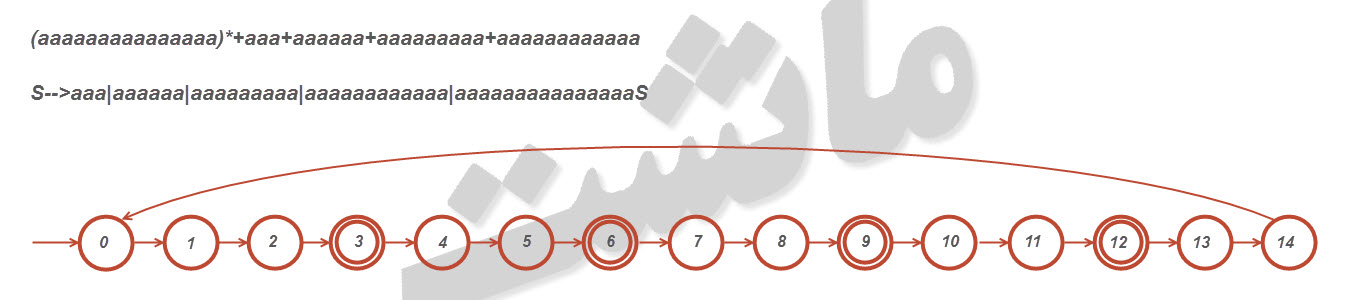
سوال: آیا برای هر زبان بصورت [tex]a^{n}[/tex] که n مضربی از x باشد اما مضربی از y نباشد، نقطه x*y همان نقطه شروع است؟(تشکیل حلقه)
منظم است.(n مضربی از ۳ باشد اما مضربی از ۵ نباشد)

سوال: آیا برای هر زبان بصورت [tex]a^{n}[/tex] که n مضربی از x باشد اما مضربی از y نباشد، نقطه x*y همان نقطه شروع است؟(تشکیل حلقه)
Can I see some ID?
Feeling left out?
نگران نباش، فقط روی این لینک برای ثبت نام کلیک کن. رمزت رو فراموش کردی؟ اینجا به یادت میاریم! close

